
第八章向量代数与空间解析几何第二节数量积只向量积两向量的数量积两向量的向量积08
第八章 向量代数与空间解析几何 第二节 数量积 向量积 一、两向量的数量积 二、两向量的向量积

引言1、二阶行列式a12a1定义日由四个数排成一行二列(横排称行、竖排称列)的数表a21a22称为二阶行列式数a,称为行列式的第i行第i列的元素,i为行标,i为列标aa12计算: D == aiα22 - a12^21a21a222、三阶行列式定义由九个数排成三行三列(横排称行、竖排称列)的数表anla13a122α23称为三阶行列式,a21a31a32a33o个不个高等数学教学部不不个
高等数学教学部 2
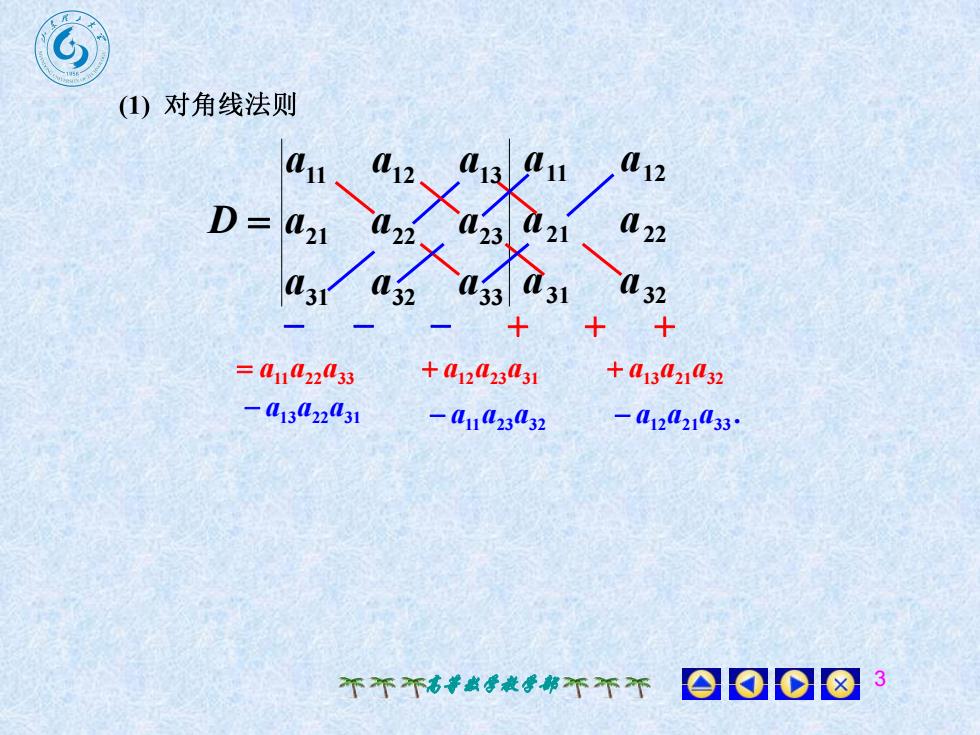
(1)对角线法则a12ana12an113D=a22(21a22a23a21a31a321'32d31a'33+++=a1122433+a13a21a32+a12a2331-a13/2231-anA23ll32-ai2a21a33:3008个个个高等数学教学部不不不
高等数学教学部 3 31 32 21 22 11 12 a a a a a a 31 32 33 21 22 23 11 12 13 a a a a a a a a a D a11a23a32 a11a22a33 a12a23a31 a13a21a32 . a12a21a33 a13a22a31
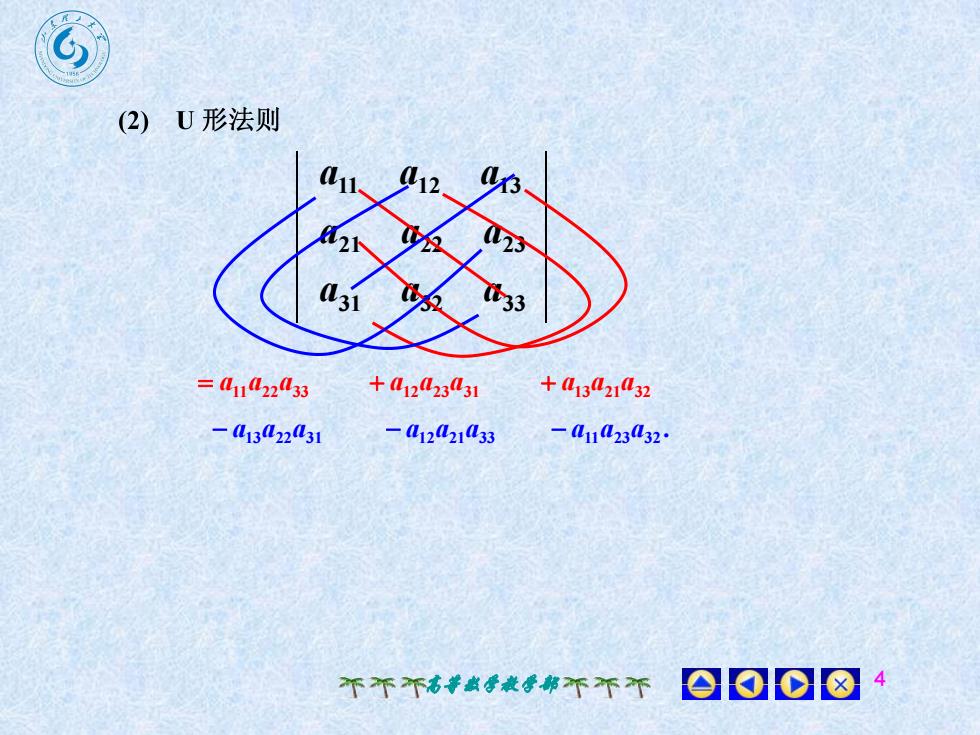
(2)U 形法则aX3aua12(2321(31033= ai1a22l33+a12a23a31+13a2132 a13(22A31- a1221l33- a11a23A32:0010个个个高等数学教学部个不个
高等数学教学部 4 31 32 33 21 22 23 11 12 13 a a a a a a a a a a11a22a33 . a11a23a32 a12a23a31 a13a21a32 a13a22a31 a12a21a33
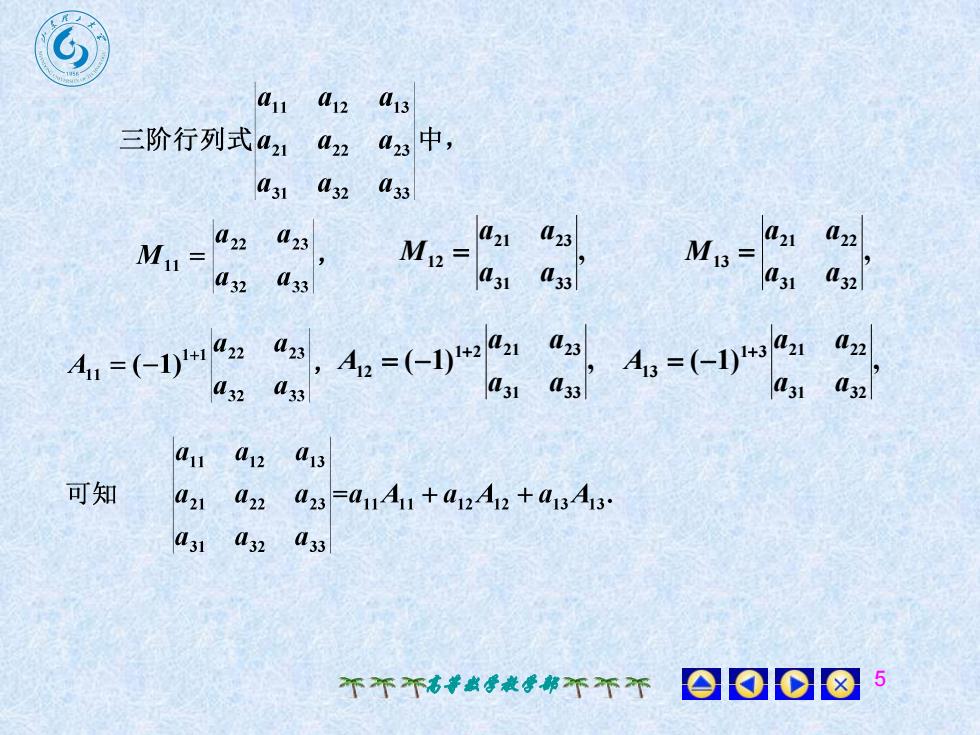
Caia12a13中,三阶行列式a21a23a22a31a33a32a21a21a22a123a22a23M13Mi2 =Mi-a31a33a32a31a33a32a21a21a22a23a22a23A13 =(-1)1+3A12 =(-1)1+2A =(-1)+1a31a31(33a32a32a33aua12a13可知a21a22=a11A11 +a12A12 +a13A13a23a31a32a33oo8个个个高等数学教学部不不不
高等数学教学部 5 , 31 33 21 23 12 a a a a M , 31 32 21 22 13 a a a a M ( 1) , 31 33 1 2 21 23 12 a a a a A ( 1) , 31 32 1 3 21 22 13 a a a a A

32例 1 计算行列式D =1+解 D=2(-1)+ 3(-1)-27-oo8个个个高等数学教学部
高等数学教学部 6 1 2 2 1 2( 1) 11 D 4 2 1 1 ( 1)( 1) 1 2 4 1 1 2 3( 1) 1 3 27

-两向量的数量积1、定义引例一物体在常力F作用下沿直线从点M移动到点M,表示位移,则力F所做的功为FW=F IIsIcoso电路M,3M,定义1给定向量a与b,将[a与|bl及它们的夹角的余弦的乘积,称为向量a与b的数量积,记作a.b,即 a·b=ailblcoso.由引例知, W = F.s.a008个不个高等数学教学部不不个
高等数学教学部 7 s F M1 M2 W | F || s | cos a b | a || b | cos . a b

S说明(l) a.a=ap..a.a=allalcoso=ap证 :0= 0,(2) a-b =lal1 cos(a,b) =la/Prj,5, Pri,6_4-b.lal(3) alb←= a.b=0 (a±0,b+0)证(-) ::a·b=0, lallbcoso=0,.coso=0, 0-元,..alb.2'(-) -41b 0-g ..coso =0, a.b=ablcoso =0001018个不不高教学教学部不不不
高等数学教学部 8 (2) a b | a || b | cos(a , b) (3) a b () a b 0, cos 0, a b. (1) | | . 2 a a a () a b, cos 0, a b | a || b | cos 0. 0, | || | cos | | . 2 a a a a a , 2 ( 0, 0). a b 0 a b , 2 . | | Pr a a b ja b | a || b | cos 0, | a | Pr j b, a

62、运算律(1)交换律a.b =b.a;(aa).b = a.(ab)= a(a.b);(2)结合律证=0时,显然成立;a >0时, (aa).b=| aal-|b/·cos(aa,b)=a[a]-|b/.cos(a,b)= n(a.b);a.(ab) =lal-/ ab /.cos(a, ab) =al-/b}-cos(a,b) = a(a.b);a<0时, (aa).b =| aa}.|b/.cos(aa,b)=-[al-|b·cos(元-(a,b)=alal-lbj.cos(a,b) = a(a.b);a.(ab) ={a[-| ab}.cos(a, ab) =-[a]-[b[.cos(π -(a,b)= n(a. b).001018中个不不高教学教学部不不不
高等数学教学部 9 a b b a; ( a) b a ( b) (a b); a b ( ) | | | | cos( , ) a b a b | | | | cos( , ) a b a b (a b); a ( b) | | | | cos( , ) a b a b | | | | cos( , ) a b a b (a b); a b ( ) | | | | cos( , ) a b a b | | | | cos( ( , )) a b a b | | | | cos( , ) a b a b (a b); a ( b) | | | | cos( , ) a b a b | | | | cos( ( , )) a b a b (a b).

(a+b).c=a.c+b.c.(3)分配律证 (a+b).c =c|Prj.(a+b) =cl(Prj,a+Prjb)=lciPr j.a+lciPrj.b =a.c+b.c.000810个个个高等数学教学部不不个
高等数学教学部 10 (a b) c a c b c. a b c ( ) | c | Pr j (a b) c | c |(Pr j a Pr j b) c c c j ca c j cb | | Pr | | Pr a c b c.