
第八章第二节数量积向量积*混合积一、两向量的数量积二、两向量的向量积*三、向量的混合积HIGH EDUCATION PRESS返回结束机动自录上页下页
*三、向量的混合积 第二节 一、两向量的数量积 二、两向量的向量积 机动 目录 上页 下页 返回 结束 数量积 向量积 *混合积 第八章

两向量的数量积一、市引例设一物体在常力 F作用下,沿与力夹角为0位移为,则力F所做的功为的直线移动,W =|F 3|cos 01.定义6M,MS设向量a,b的夹角为0,称记作a.b[alb|cos 0W=F.s为a与b的数量积(点积)HIGH EDUCATION PRESS返回结束机动目录上页下页
M1 一、两向量的数量积 沿与力夹角为 的直线移动, W = 1. 定义 设向量 的夹角为 ,称 记作 数量积 (点积) . 引例. 设一物体在常力 F 作用下, 位移为 s , 则力F 所做的功为 F s cos W F s = M 2 a b 为a与b的 a , b s 机动 目录 上页 下页 返回 结束

当a≠o时,b在a上的投影为Prjab = |b|cos06TO故文a.b=aPrjaba同理,当b±0时a.b=bPrjsaa±0,b+02. 性质则a.b=0() a.a=la2则有(2)α,b为两个非零向量,元a.b=0alba,b)一12HIGH EDUCATION PRESS上页下页返回结束机动自录
b 在 a 上的投影为 故 同 理 ,当 0 时, b 2. 性质 为两个非零向量, 则有 b a Prj b a b = a b a Prj (1) a a = (2) a ,b a b = 0 ⊥ 则 a b = 0 a 0 , b 0 机动 目录 上页 下页 返回 结束

3.运算律a.b-b.a(1)交换律6a结合律(α,μ为实数)(2)(a+b)(aa).b=a.(ab)=a(a.b)C(aa)·(μb) =a(a.(μb))Prjc a Prj.b=μ(a.b)Prjc(a+b)(3)分配律(a+b).c=a.c+b.c事实上,当= 时,显然成立;当→0时(a+b) =|Prj(a+b)=|cl(Prja+Prj)=|Prjea+Prjb =a. +b.cHIGH EDUCATION PRESS目录上页下页返回结束机动
3. 运算律 (1) 交换律 (2) 结合律 a ( b) ( a ) ( b ) = ( a ( b ) ) = ( a b ) (3) 分配律 事实上, 当 c = 0 时, 显然成立 ; 当c 0时 c ( a + b ) b a bc a Prj c Prj ( a + b ) c ( a b ) c = c Prj + = c ( a b ) c c Prj + Prj a c = c Prj b c + c Prj = a c + b c Prj ( a b ) c + 机动 目录 上页 下页 返回 结束

例1.证明三角形余弦定理c2 = α2+b2 _2abcos0-6证:如图.设9CB=a, CA=b, AB=c则c=a-baB(a-b)=a.a +b.b-2a.b2=(a-b) (=+-2cosa=|l,b=|b],c=|,2 =α2+b2-2abcos0HIGH EDUCATION PRESS上页下页返回结束机动自录
A B C a b c 例1. 证明三角形余弦定理 2 cos 2 2 2 c = a + b − a b 证: 则 2 cos 2 2 2 c = a + b − a b 如图 . 设 C B = a , C A = b , AB = c = 2 c ( a − b ) ( a − b ) = a a + b b − 2 a b 2 = a 2 + b − 2 a b cos a = a , b = b , c = c 机动 目录 上页 下页 返回 结束

4.数量积的坐标表示设a=axi+ayj+a,k,b=bi+bj+b,k,则a.b=(a,i+a, j+a, k).(b,i+b, j+b,k).i=j.j=k.=l,i.j=j.k=k.i=0a.b=axbx+a,b,+a,b两向量的夹角公式当a,b为非零向量时,由于a.=abcos,得a,bx +a,b, +a.b.a.bcOsO一ailbb,+bHIGH EDUCATION PRESS上页下页返回结束机动自录
4. 数量积的坐标表示 设 则 = 0 x x y y z z = a b + a b + a b 当 为非零向量时, cos = = x x y y z z a b + a b + a b 2 2 2 x y z a + a + a 2 2 2 x y z b + b + b 由于 a b cos a a i a j a k , = x + y + z b b i b j b k , = x + y + z ( a i + a j + a k ) x y z ( b i b j b k ) x + y + z i j = j k = k i a b a b 两向量的夹角公式 , 得 机动 目录 上页 下页 返回 结束

例2. 已知三点 M(1,1,1), A(2,2,1),B(2,1,2), 求ZAMB解:MA=(1, 1, 0), MB =(1, 0,1)BCOS LAMB=_MA.MBM则MAMB1+0+0V2 V22元故AMB=3HIGH EDUCATION PRESS机动上页下页返回结束自录
M A = ( ), M B = ( ) = B M 例2. 已知三点 M (1,1,1), A( 2 , 2 ,1) , B( 2 ,1 , 2 ), AMB . A 解: 1, 1, 0 1, 0, 1 则 cos AMB = 1+ 0 +0 2 2 AMB = 求 M A M B MA MB 故 机动 目录 上页 下页 返回 结束
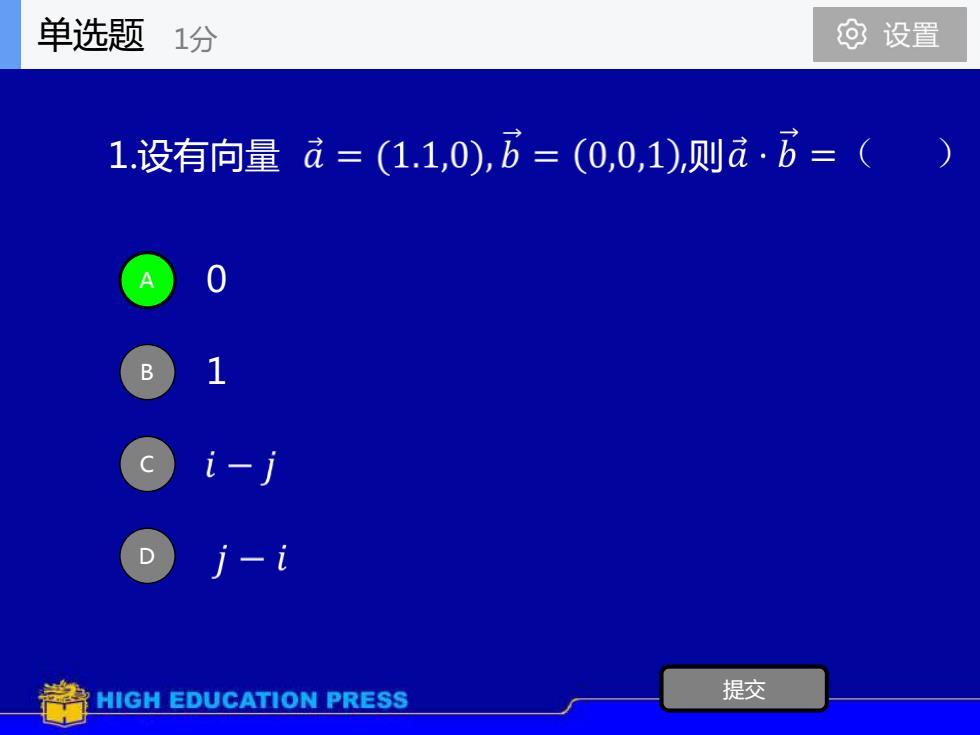
单选题0设置1分a= (1.1,0),b = (0,0,1),则a. b = ( 1.设有向量O1B一提交HIGH EDUCATION PRESS
1.设有向量 ,则 A 0 B 1 C D 提交 单选题 1分
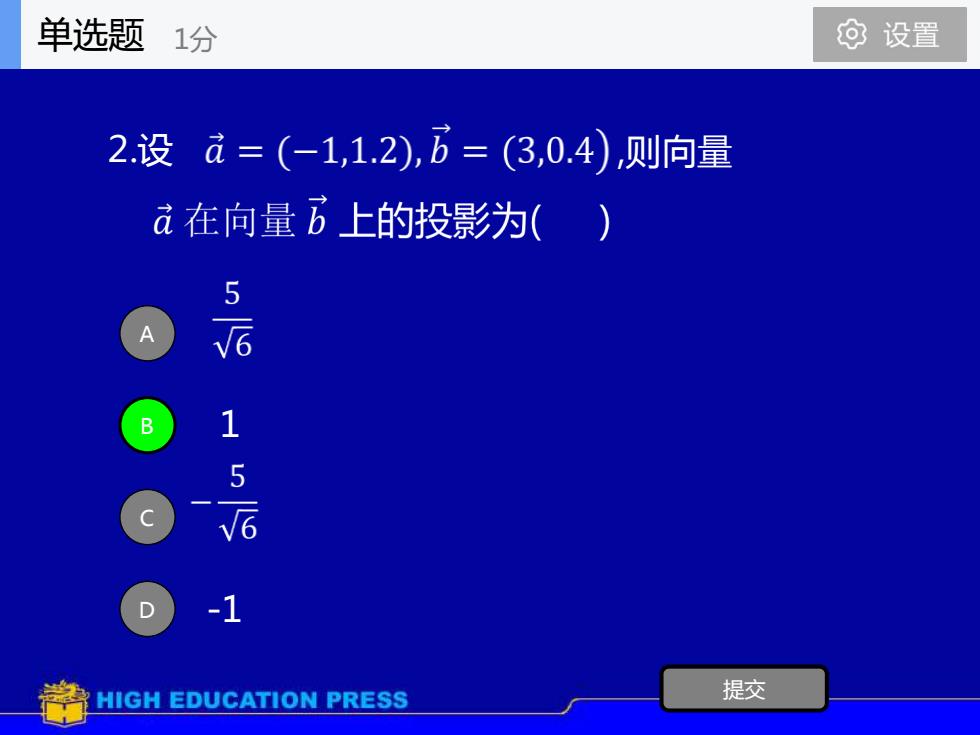
单选题0设置1分2.设a = (-1,1.2),b = (3,0.4),则向量a在向量 b 上的投影为(5T615V6提交HIGH EDUCATION PRESS
2.设 ,则向量 A B 1 C D -1 提交 单选题 1分
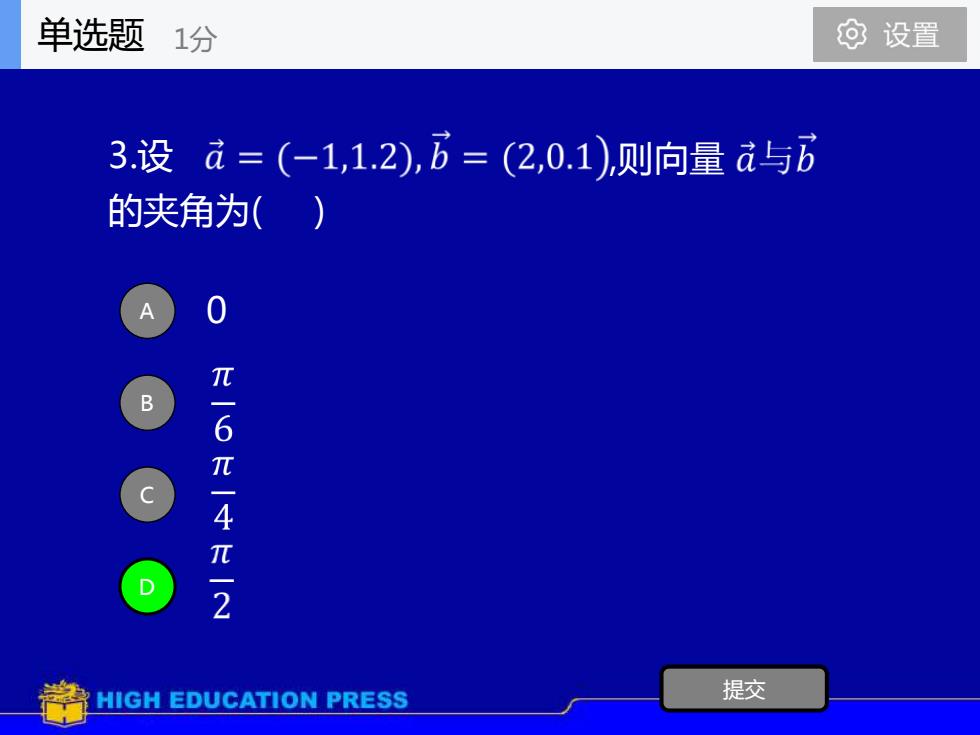
单选题0设置1分3.设a = (-1,1.2),b = (2,0.1),则向量 a与b的夹角为(元-6元-4元-2B提交HIGH EDUCATION PRESS
3.设 ,则向量 的夹角为( ) A 0 B C D 提交 单选题 1分