
中国农业大学 第八讲垂直问题、平面应用及综合问题 p124-132 预习:P133-135 工程制图与计算机图学研究室
工程制图与计算机图学研究室 中国农业大学图形研究室 第八讲 垂直问题、平面应用及综合问题 预习:P133-135 p124-132

§4-3 垂直问题 中国农业大学 立体几何定理: 一、直线与平面垂直 (1)若直线垂直平面内任意二相 1几何条件 交直线,则直线垂直该平面。 (2)若直线垂直一平面,则必垂 直于该平面上的一切直线。 工程制图与计算机图学研究室
工程制图与计算机图学研究室 中国农业大学图形研究室 §4-3 垂直问题 一、直线与平面垂直 1 几何条件 立体几何定理: (1) 若直线垂直平面内任意二相 交直线,则直线垂直该平面。 (2) 若直线垂直一平面,则必垂 直于该平面上的一切直线
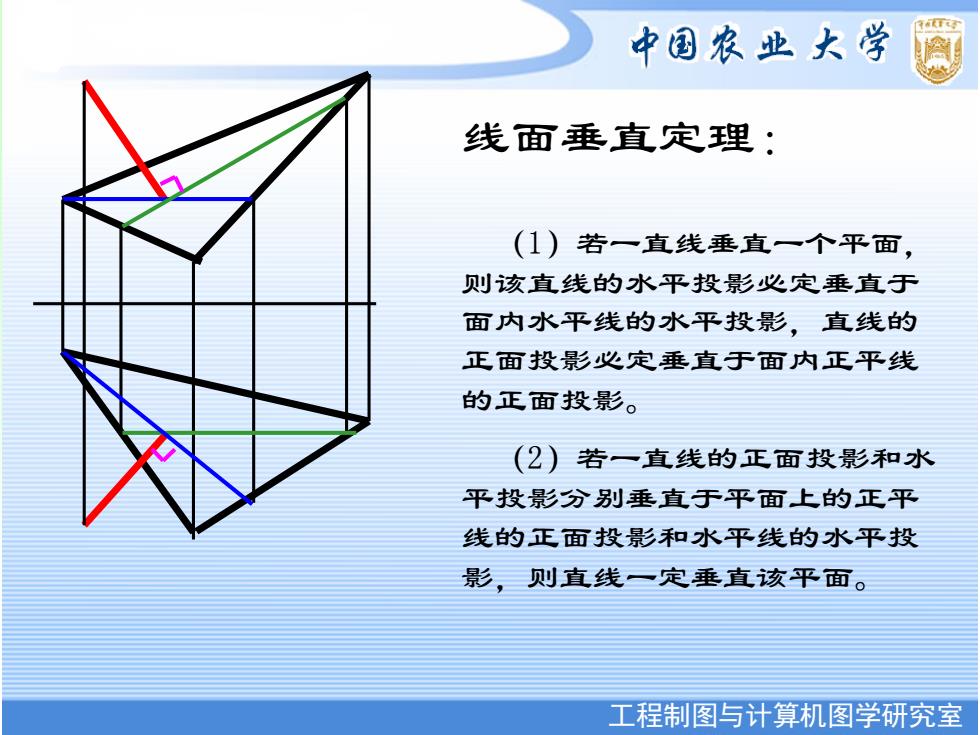
中国农业大学 线面垂直定理: (1)若一直线垂直一个平面, 则该直线的水平投影必定垂直于 面内水平线的水平投影,直线的 正面投影必定垂直于面内正平线 的正面投影。 (2)若一直线的正面投影和水 平投影分别垂直于平面上的正平 线的正面投影和水平线的水平投 影,则直线一定垂直该平面。 工程制图与计算机图学研究室
工程制图与计算机图学研究室 中国农业大学图形研究室 线面垂直定理: (1)若一直线垂直一个平面, 则该直线的水平投影必定垂直于 面内水平线的水平投影,直线的 正面投影必定垂直于面内正平线 的正面投影。 (2)若一直线的正面投影和水 平投影分别垂直于平面上的正平 线的正面投影和水平线的水平投 影,则直线一定垂直该平面
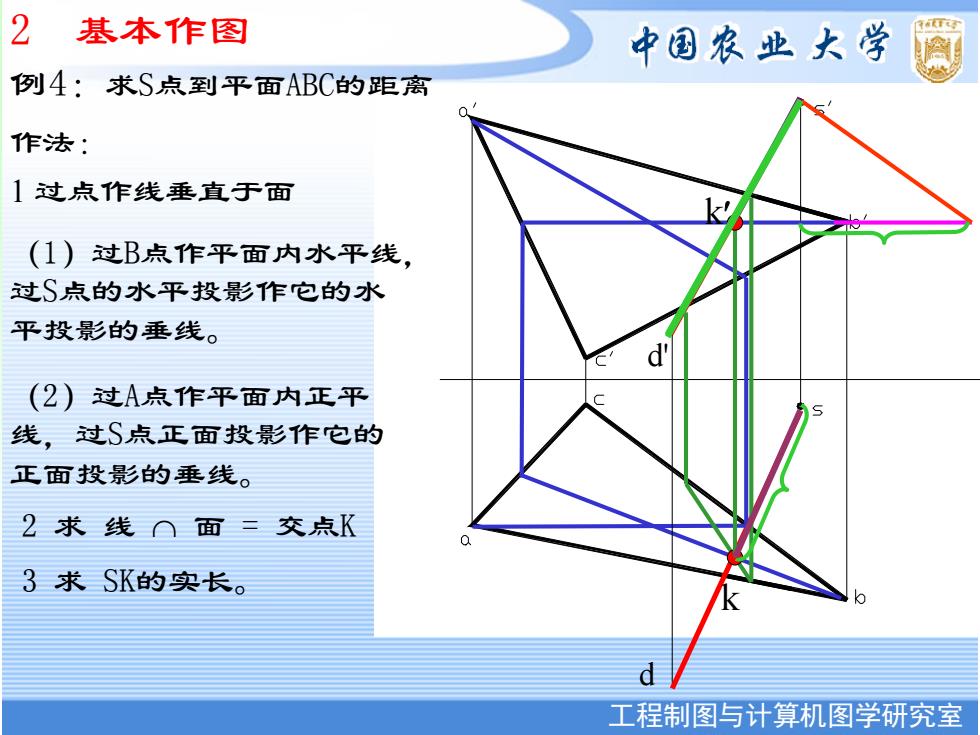
2 基本作图 中国农业大学 例A::求S点到平面ABC的距离 作法: 1过点作线垂直于面 (1)过B点作平面内水平线, 过S点的水平投影作它的水 平投影的垂线。 d (2)过A点作平面内正平 线,过S点正面投影作它的 正面投影的垂线。 2求线∩面=交点K 3求SK的实长。 d 工程制图与计算机图学研究室
工程制图与计算机图学研究室 中国农业大学图形研究室 作法: 1 过点作线垂直于面 (1)过B点作平面内水平线, 过S点的水平投影作它的水 平投影的垂线。 (2)过A点作平面内正平 线,过S点正面投影作它的 正面投影的垂线。 2 求 线 面 = 交点K 3 求 SK的实长。 k k d' d 2 基本作图 例4:求S点到平面ABC的距离
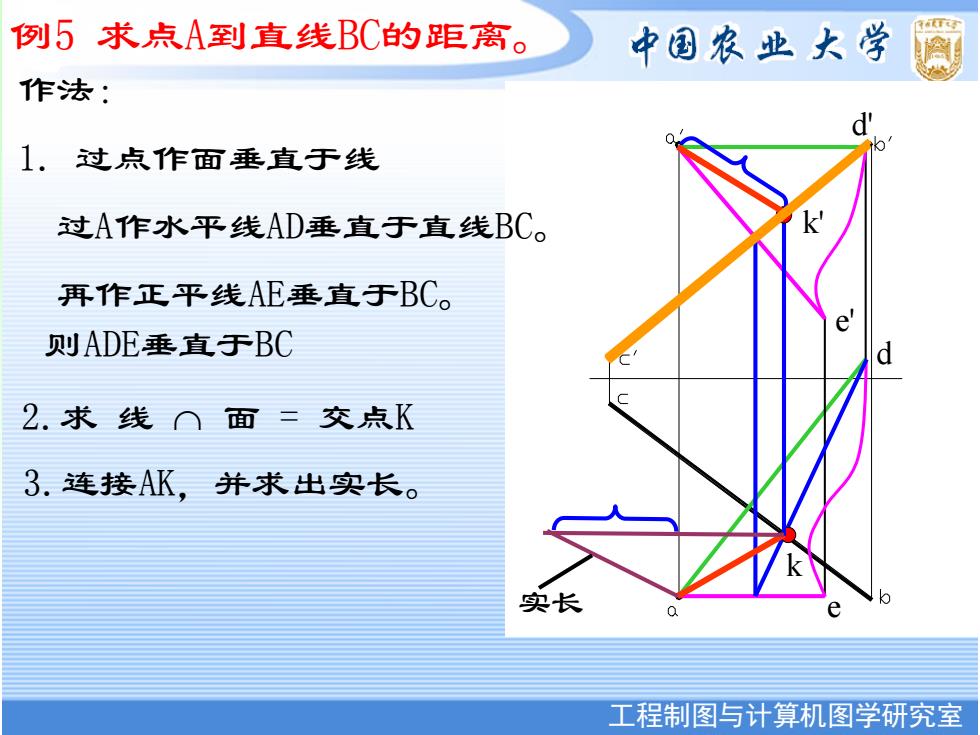
例5求点A到直线BC的距离。 中国农业大学 作法: 1.过点作面垂直于线 过A作水平线AD垂直于直线BC。 再作正平线AE垂直于BC。 e 则ADE垂直于BC 2.求线∩面三交点K 3.连接AK,并求出实长。 实长 工程制图与计算机图学研究室
工程制图与计算机图学研究室 中国农业大学图形研究室 例5 求点A到直线BC的距离。 作法: 1. 过点作面垂直于线 过A作水平线AD垂直于直线BC。 再作正平线AE垂直于BC。 2.求 线 面 = 交点K 3.连接AK,并求出实长。 k' k d d' e e' 则ADE垂直于BC 实长
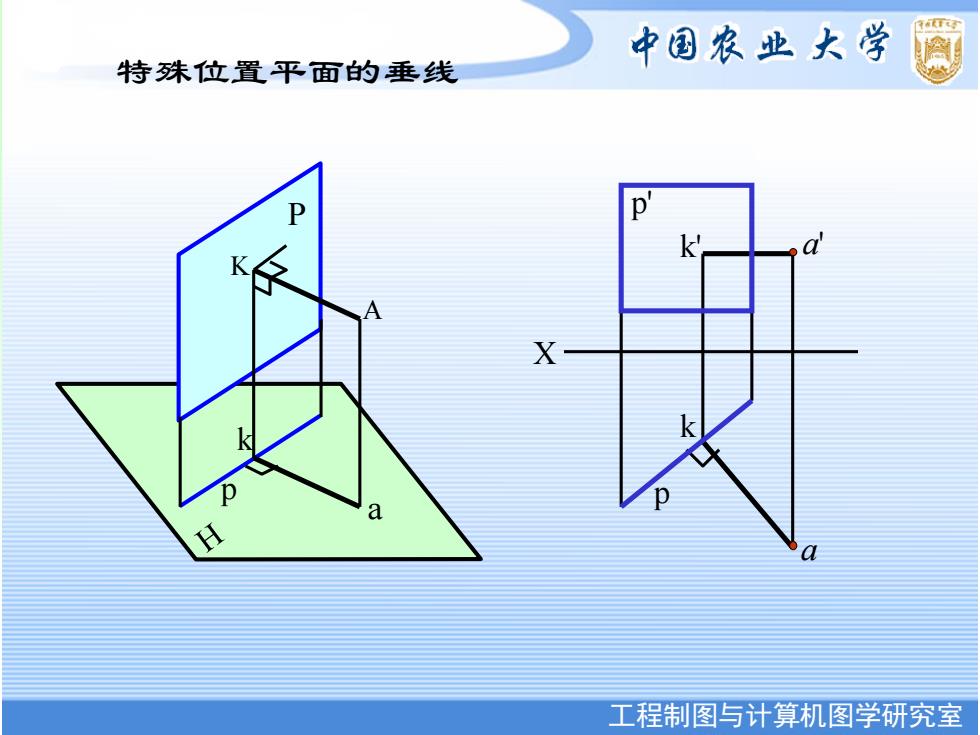
中国农业大学 特殊位置平面的垂线 p k X 工程制图与计算机图学研究室
工程制图与计算机图学研究室 中国农业大学图形研究室 B C P K A k a p k X p p' k' a' a 特殊位置平面的垂线
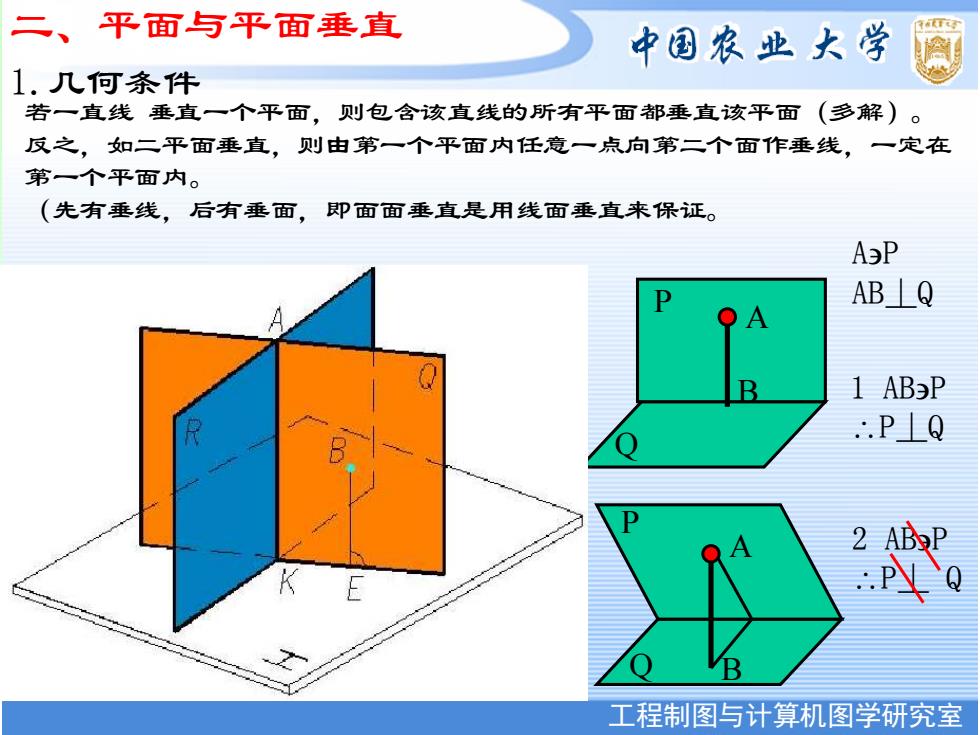
二、平面与平面垂直 中国农业大学 1.几何条件 若一直线垂直一个平面,则包含该直线的所有平面都垂直该平面(多解)。 反之,如二平面垂直,则由第一个平面内任意一点向第二个面作垂线,一定在 第一个平面内。 (先有垂线,后有垂面,即面面垂直是用线面垂直来保证。 AP AB⊥Q 1 ABP ·P⊥Q PV 工程制图与计算机图学研究室
工程制图与计算机图学研究室 中国农业大学图形研究室 P Q P Q 二、平面与平面垂直 1.几何条件 若一直线 垂直一个平面,则包含该直线的所有平面都垂直该平面(多解)。 反之,如二平面垂直,则由第一个平面内任意一点向第二个面作垂线,一定在 第一个平面内。 (先有垂线,后有垂面,即面面垂直是用线面垂直来保证。 A B A B AP AB⊥Q 1 ABP P⊥Q 2 ABP P⊥ Q
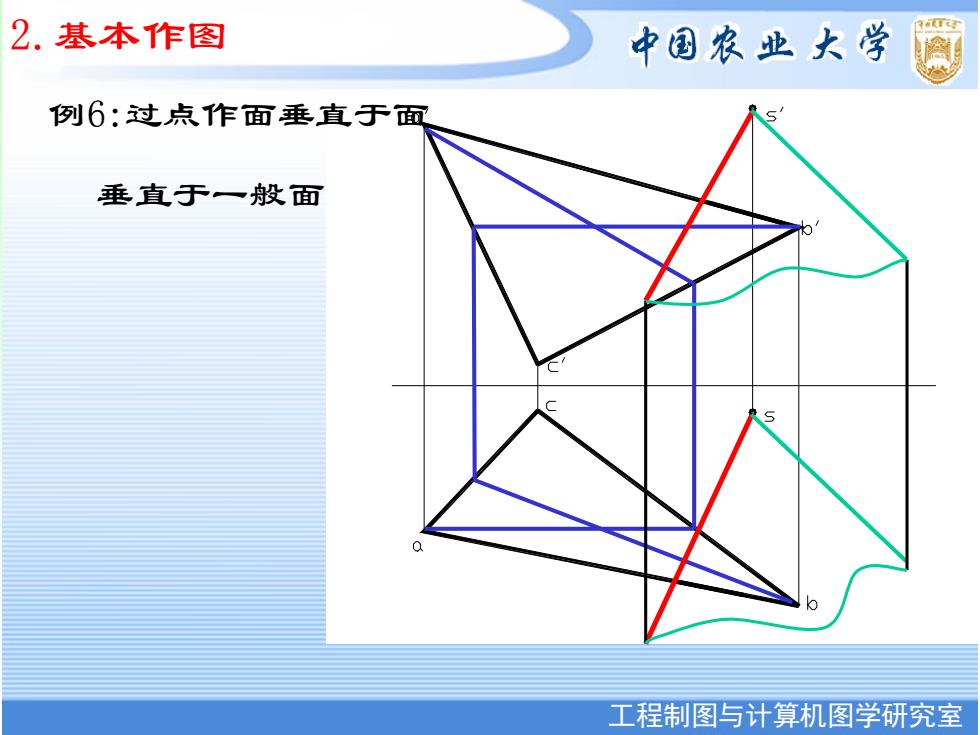
2.基本作图 中国农业大学 例6:过点作面垂直于面 垂直于一般面 工程制图与计算机图学研究室
工程制图与计算机图学研究室 中国农业大学图形研究室 2.基本作图 例6:过点作面垂直于面 垂直于一般面

例7:过点作面垂直于面 中国农业大学 垂直于正垂面 工程制图与计算机图学研究室
工程制图与计算机图学研究室 中国农业大学图形研究室 k' k a b c a' c' b' x 垂直于正垂面 e' m' e m 例7:过点作面垂直于面

中国农业大学 特殊位置平面的垂直 p ⊙ A b X 工程制图与计算机图学研究室
工程制图与计算机图学研究室 中国农业大学图形研究室 C p P Q A B b a q p q C p' q' X 特殊位置平面的垂直