
lim课前练习:nn→

第3讲常用极限计算方法山东理工大学李海玲
第3讲 常用极限计算方法 山东理工大学 李海玲
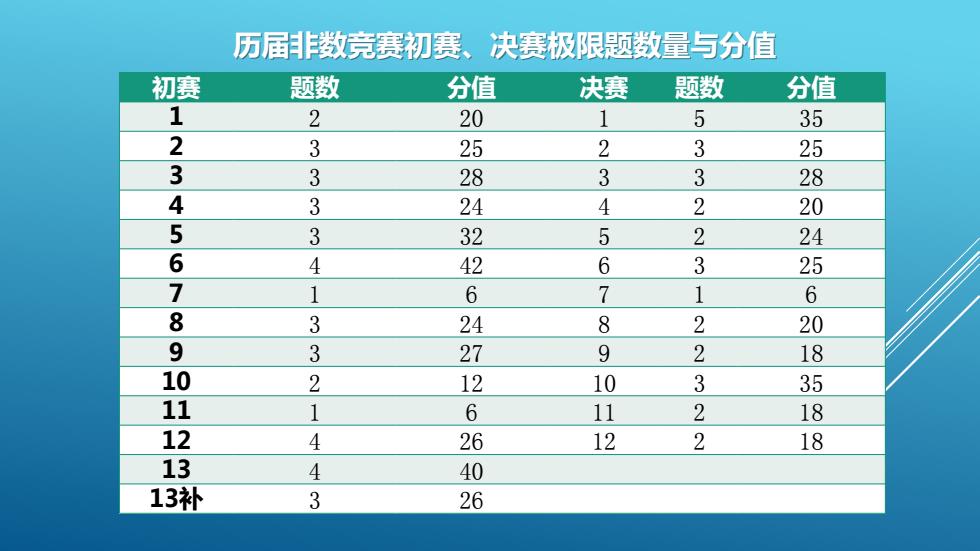
历属非数竞赛初赛、决赛极限题数量与分值决赛初赛题数分值题数分值1251352023232525333328284342242053523224646342257167168328202493922718102312103511162111812241218261344013补326
初赛 题数 分值 决赛 题数 分值 1 2 20 1 5 35 2 3 25 2 3 25 3 3 28 3 3 28 4 3 24 4 2 20 5 3 32 5 2 24 6 4 42 6 3 25 7 1 6 7 1 6 8 3 24 8 2 20 9 3 27 9 2 18 10 2 12 10 3 35 11 1 6 11 2 18 12 4 26 12 2 18 13 4 40 13补 3 26 历届非数竞赛初赛、决赛极限题数量与分值
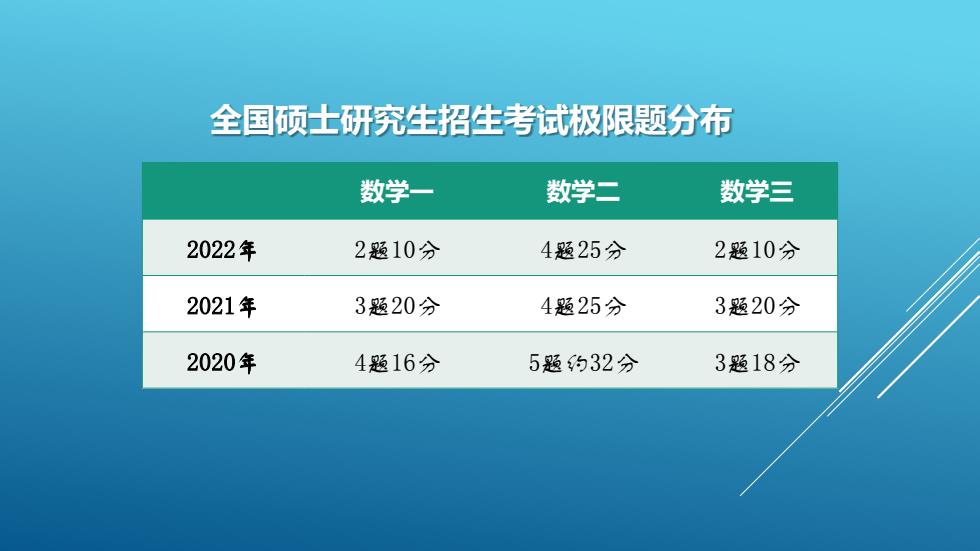
全国硕士研究生招生考试极限题分布数学一数学二数学三2022年2题10分4题25分2题10分2021年3题20分4题25分3题20分2020年4题16分5题约32分3题18分
全国硕士研究生招生考试极限题分布 数学一 数学二 数学三 2022年 2题10分 4题25分 2题10分 2021年 3题20分 4题25分 3题20分 2020年 4题16分 5题约32分 3题18分

常用极限计算方法、题型与典型题分析海涅定理(极限的归一性,归结原则)定理1lim f(x)= A对于任何满足xn →+8(n → 8)的数列x→+o{xn},均有limf(xn)= An-定理2lim f(x)= A 对于任何满足xn → xo(n → ) 且xn ± xox→xo(n = 1,2,..)的数列(xn),均有 lim f(xn)= A
常用极限计算方法、题型与典型题分析 海涅定理(极限的归一性,归结原则)

常用极限计算方法、题型与典型题分析极限的定义数列定义的等价描述形式定义1:liman =α V>0,N z+,恒有lan-αlNn-0定义2:Vn>N成立 lanalO,ENZn-8成立[an -al Nn-→定义4:成立|an-alO,N ZVn >Nn-→α其中M是一个与&和n都无关的正常数
常用极限计算方法、题型与典型题分析 数列定义的等价描述形式 1、极限的定义

常用极限计算方法、题型与典型题分析1、极限的定义定义1:liman =α >0,Nz,当n> N,恒有lan-αl0(或在叙述过程中适当时候取V);(2)令[αn 一αl β()(找 N的关键步骤,一般需要放大);(4)取N=[β()l,再用一N语言叙述并下结论
常用极限计算方法、题型与典型题分析 1、极限的定义

常用极限计算方法、题型与典型题分析a+a,+a+limlima例1:证明柯西数列极限命题=a→=ann-→8n-x【提示】:由题设可知,Vε>0,NZ+,当n>N时,恒有α-αN,时,有取N=maxa+a,+·.-<2eRn
常用极限计算方法、题型与典型题分析

常用极限计算方法、题型与典型题分析1、极限的定义lim f(x) = A一 Vε > 0, X >0, 当 x>X 时, If(x)-A| 0, X >0, 当x0, X>0, 当[x| >X时, If(x) -A|0, 38> 0, 当 00, 38 > 0, 当 -S 0, 38> 0,X-→Xo当0<|x-xol <8时, If(x)-A|<ε
常用极限计算方法、题型与典型题分析 1、极限的定义

常用极限计算方法、题型与典型题分析2、极限的四则运算法则定理(四则运算的极限)假定下面考虑的都是对自变量x的同一变化过程的极限.设limf(x)和limg(x)存在,则(1) lim[f(x) ±g(x)) = limf(x) ± limg(x);(2) lim[f(x)g(x))= limf(x)limg(x);f(x)limf(x)(3) lim(limg(x) ± 0).g(x)limg(x)特别,lim[Cf(x)] = Climf(x),其中C为常数lim[f(x)]n=[limf(x)]n,其中n为正整数
常用极限计算方法、题型与典型题分析 特别, 2、极限的四则运算法则