
de fo(o?-1)eo"dp.练习题1:计算I=练习题2:设是球面(α-1)+(-1) +(-1) =4,计算曲面积分I = $f(α2 +y2 +3)ds.Z
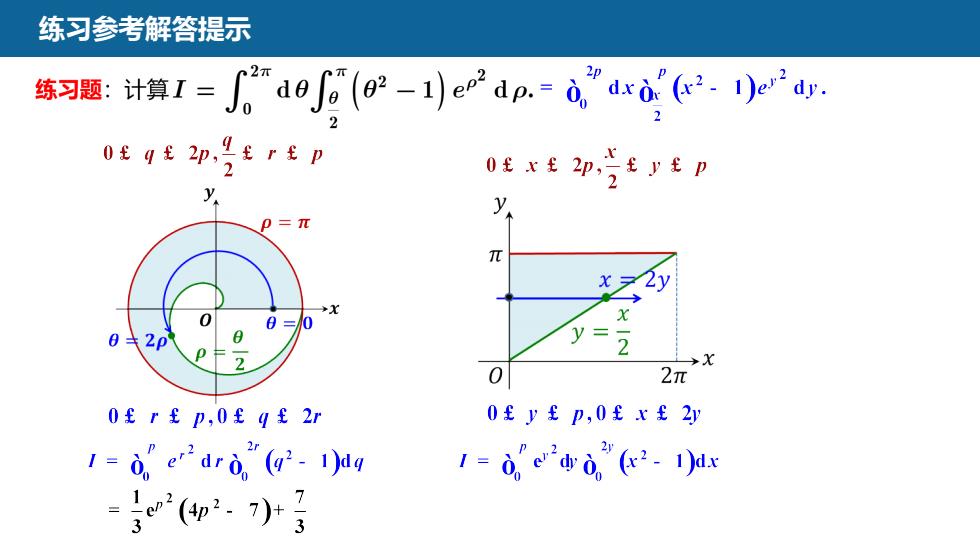
练习参考解答提示?2元) ep" dp. = 0 dxo" (x?. 1)ex? dyA2-11练习题:计算I=de024trtpfqf2pTofxttyp2p2yTX+xx00二0062p20-2>x02元ofy,ofx2y0frfp,0fgf2r e' dy o.dr (x2- )d)-1dq
练习参考解答提示

第7讲多元函数积分学及其应用山东理工大学李海玲
第7讲 多元函数积分学及其应用 山东理工大学 李海玲

积分区域的分类与积分的基本计算法二积分区域的对称性与积分的计算性质三、多元函数积分计算的一般思路与方法
l 一、积分区域的分类与积分的基本计算法 l 二、积分区域的对称性与积分的计算性质 l 三、多元函数积分计算的一般思路与方法

积分区域的分类与积分的基本计算法直角坐标系下平面区域的分类(X-型、Y-型)1ytyy = y2(x)= y2(x)DDDDD1CDXbx0aaxbarx0XObx0aCD3= yi(x)Vy=yi(αx非X-型区域分割X-型区域a≤x≤blyi(x) ≤y ≤ y2 (x)V2(xf (x,y )d)00f (x, )ds = . dx o"D
一、积分区域的分类与积分的基本计算法 直角坐标系下平面区域的分类(X-型、Y-型) X-型区域 非X-型区域分割
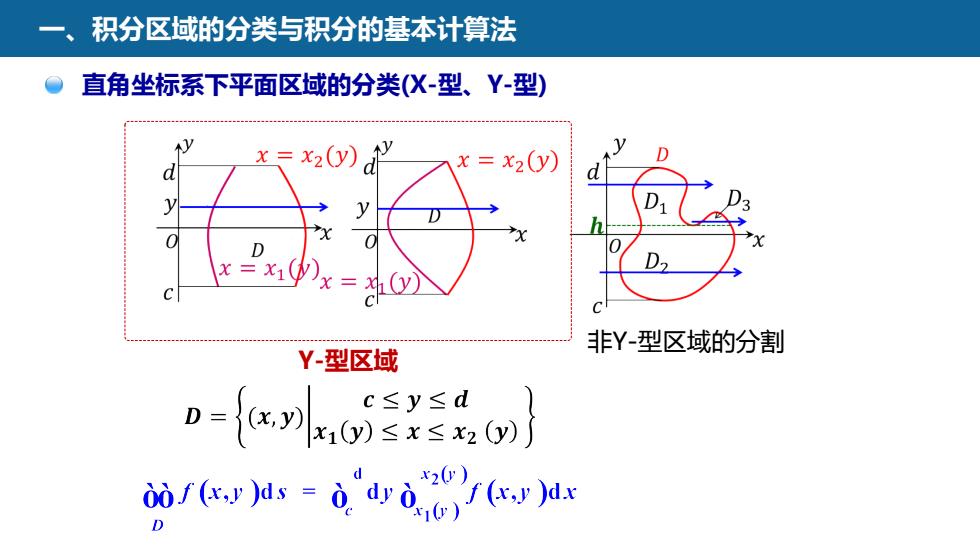
积分区域的分类与积分的基本计算法直角坐标系下平面区域的分类(X-型、Y-型)x = x2(y)= x2(y)0dDyDhXC0XDC非Y-型区域的分割Y-型区域c≤y≤dx1(y) ≤ x ≤ x2 (y)f (x,y )d.0of (x,y )ds = o"dy o.D
一、积分区域的分类与积分的基本计算法 非Y-型区域的分割 直角坐标系下平面区域的分类(X-型、Y-型) Y-型区域
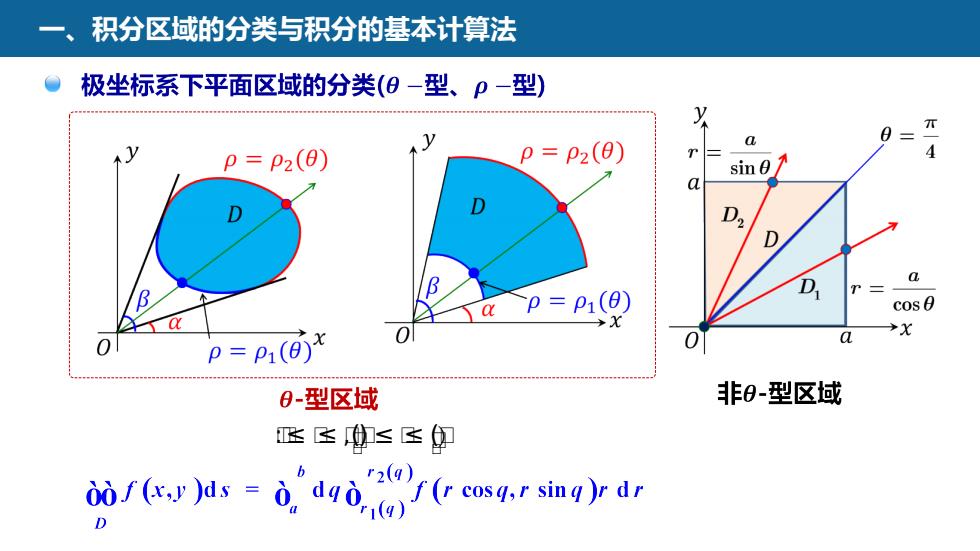
积分区域的分类与积分的基本计算法极坐标系下平面区域的分类(O一型、P一型)y元02ap = P2(0)4rp= P2(0)sineaD,DaDBr=p = Pi(0)1cosaαXa+xo0a0p = P1(0)非-型区域Q-型区域民风风0of (x,y )ds = o, dqo.f (r cosq,r sinq)r drri(yD
一、积分区域的分类与积分的基本计算法 ᵽ:≤ ᵽ≤ ᵽ,ᵽᵽ (ᵽ) ≤ ᵽ≤ ᵽᵽ (ᵽ)
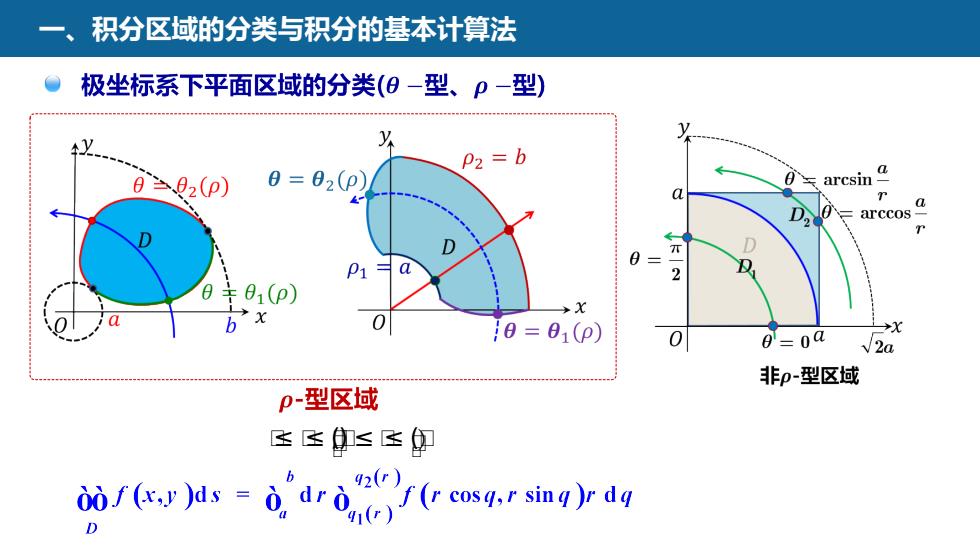
积分区域的分类与积分的基本计算法极坐标系下平面区域的分类(-型、P一型)14yP2=b0=02(p)arcsin9车0=42(p)aaDo=arccos2DD元0DP1 =a2(p)xbx0+x10 = 01(p)0g=oaJ2a非p-型区域p-型区域风00 f (x,y )ds = 0' dr o"2'f(r cosq,r sing )r dqD
一、积分区域的分类与积分的基本计算法 ᵽ≤ ᵽ≤ ᵽ,ᵽᵽ (ᵽ) ≤ ᵽ≤ ᵽᵽ (ᵽ)
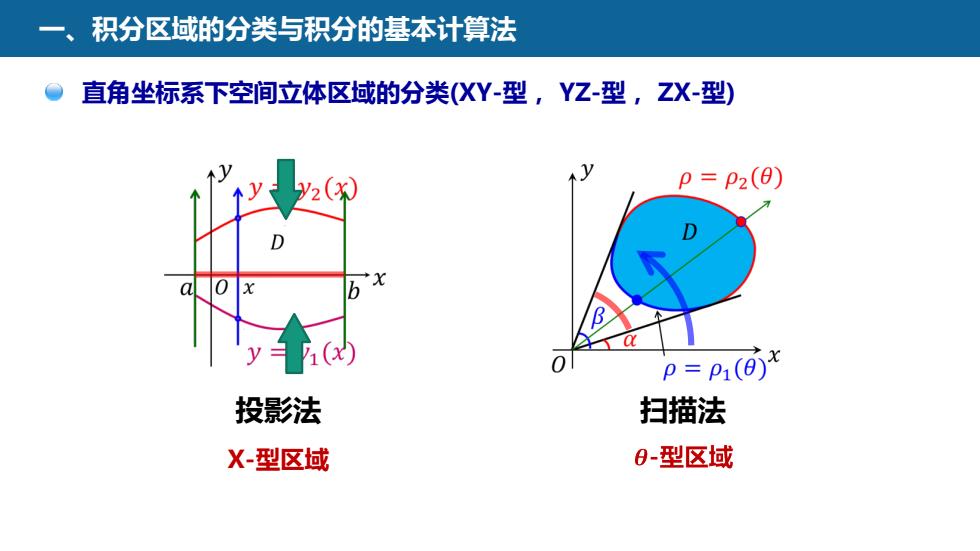
积分区域的分类与积分的基本计算法直角坐标系下空间立体区域的分类(XY-型,YZ-型,ZX-型)p = P2(0)V2(x)Dbt0xa(xp = pi()x0投影法扫描法9-型区域X-型区域
一、积分区域的分类与积分的基本计算法 直角坐标系下空间立体区域的分类(XY-型, YZ-型, ZX-型) 投影法 扫描法 X-型区域

积分区域的分类与积分的基本计算法直角坐标系下空间立体区域的分类(XY-型,YZ-型,ZX-型z = Z2(x,y)2Z=Z2(x,y)Z12z=1-x-72VD22Dxyz1(x,y)?=OxY0C(x2,2)Dxy1z=zi(x,y)XY-型区域KxW:z,(x,y)f zf z2(x,y)(x,y)i Dx)先一后二22(x,)000.f(x,y,z)ds = 00 ds o,f(x,y,z)dz投影法z1(x,y)WDxy
一、积分区域的分类与积分的基本计算法 直角坐标系下空间立体区域的分类(XY-型, YZ-型, ZX-型) XY-型区域 先一后二 投影法