
试卷代号:1024 座位号■■ 中央广播电视大学2010一2011学年度第二学期“开放本科”期末考试 信号处理原理 试题 2011年7月 题 号 二 三 四 五 六 总分 分 数 得 分 评卷人 一、判断题(每小题3分,共15分)】 1.Sa函数是奇函数。 2.平移,反褶,尺度变换是3种不同的信号运算 3.三角函数集一定不是完备的正交函数集 4.实偶信号的FT是偶函数。 5.信号时移只会对幅度谱有影响。 得分 评卷人 二、单项选择题(每小题5分,共25分) 1.卷积不具有的特性是()。 A.交换律 B.结合律 C.分配律 D.互补性 2.卷积积分f(t+3)*6(t一4)的计算结果是( )。 A.f(t+1) B.f(t-1) C.f(t-9) D.f(t+9) 181
试卷代号 座位号 I I 中央广播电视大学 1学年度第二学期"开放本科"期末考试 信号处理原理试题 2011 年7 |题号!一|二|三|四|五|六|总分| |分数 I I I I I 得分!评卷入 一、判断题(每小题 3分,共 5分) 1. Sa 2. 尺 度 是3 种不 号运算 3. 不是 4. 的Fl" 5. 会对 有 影 得分!评卷人 二、单项选择题(每小题 5分,共 5分) 1. 特性 )。 A. c. 配律 B. 结合 I). 2. 卷积 十3) )。 A. f(t c. .f(t-g) BD 181

3.下列说法正确的是()。 A,直流信号的傅立叶频谱是阶跃函数 B.(t)在t=0时,取值为零 C.复指数频谱中负频率出现是数学运算的结果,有相应的物理意义。 D.9(6(t))=1 4.离散时间系统是指输入、输出都是()的系统。 A.模拟信号 B.冲激信号 C.序列 D.矩形信号 5.Z[2"u(n)]=( )。 A年2 c产2 D 得 分 评卷人 三、填空题(每小题4分,共20分)】 1.元音表现出 的特性。 2.周期信号如图所示,这个周期信号是一个 周期信号,其傅立叶级数一定不含 有 0.5 -π/2 元12 题图1 182
3. )。 A. B. c. 复指 D. !!7 (议。 4. 统是 都是 <. )的系统。 A. B. c. D. 5. Z[2 A.2 ·z-2 得分 1. 音表 D. - _1 z-l 三、填空题(每小题 的特性。 2. 是一 10.5 周期信号,其傅立叶级数一定不含 /\ 182 -厅- ff 12 题图 17:
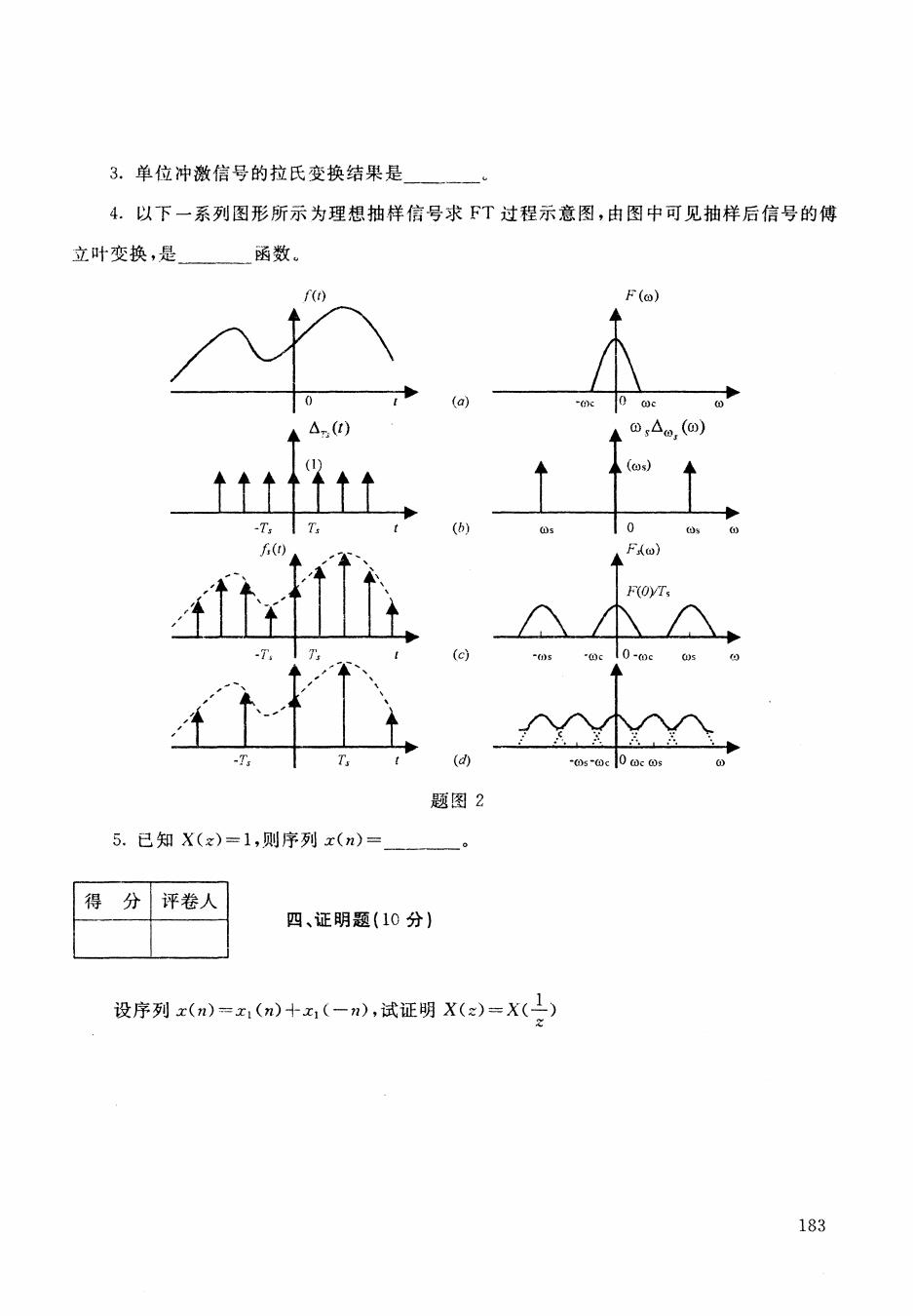
3.单位冲激信号的拉氏变换结果是 4.以下一系列图形所示为理想抽样信号求FT过程示意图,由图中可见抽样后信号的傅 立叶变换,是 函数。 f() F() 0 (a) 00c 40 (os) (b) 0 f() 、F(o) F(OyTs (c) d -0s-0c0 ac @s 题图2 5.已知X(z)=1,则序列x(n)= 得 分 评卷人 四、证明题(10分) 设序列x(n)=x(m)+x(-),试证明X(:)=X() 183
3. 结果 4. 一 系 形 所示 求FT 过程 立叶变换,是函数 ru) (a) 'nv (e) , , , ,,, z ,, , , p --5' / -Ts Ts (d) 是主 00 5. 得分|评卷人 四、证明题( 10 f-( ro (ω) (ωs) ros o (us (0 FA 设序列 =Xl (n) -I- X l (-11) z- == z 183

得 分 评卷人 五、计算题(每小题10分,共20分) 1.根据以下频谱搬移特性求取信号g(t)=cos2t的FT。 $[f(t)cos(bt)]-j[F(w-6)+F(w+b)] 2.设一阶离散系统的差分方程为ay(n)一by(n一1)=cx(n),求: (1)该系统的传递函数H() (2)输入为6(n)时系统的零状态响应。 得 分 评卷人 六、作图题(10分) 已知f(t)的波形如图所示,试绘出df(t)/dt的波形 f(t) 2 1.5 0.5 题图3 184
得分|评卷入 五、计算题(每小题 1. (t) =cos2t t ) t ) 2 2. 阶离 -by(n-l)=cx(n) (1) (2) 得分 六、作图题 已知只 波形 波形 2 1. 5 1~ f - d El Fl d , ,., ,,, t 1 2 4 5 题图 184

试卷代号:1024 中央广播电视大学2010一2011学年度第二学期“开放本科”期末考试 信号处理原理 试题答案及评分标准 (供参考) 2011年7月 一、判断题(每小题3分,共15分) 1.X 2.√ 3.X 4.√ 5.X 二、单项选择题(每小题5分,共25分) 1.D 2.B 3.D 4.C 5.C 三、填空题(每小题4分,共20分) 1.准周期信号 2.偶; 正弦项 3.1 4.周期 5.8(n) 四、证明题(10分) 证明: 因为x(n)-x(一n),由Z变换的定义有 x)=∑x0)=∑x(-) 令k=一1,得: x)-之=✉)t=Xe) 五、计算题(每小题10分,共20分) 1.解:令f(t)=1,那么F(w)=2π(w) (3分) 根据频谱搬移特性,3[f(t)cos(2)]=2[F(@-2)+F(w+2)] (4分) =合×[2mu-2)+2m(a+2)] =rd(w-2)+π6(w十2) (3分) 185
试卷代号: 1024 中央广播电视大学 1学年度第二学期"开放本科"期末考试 信号处理原理试题答案及评分标准 (供参考) 2011 年7 一、判断题(每小题 1. X 2. V 3. X 二、单项选择题(每小题 4.V 5. X 1. D 2. B 3. I) 4. C 5. C 三、填空题(每小题 2 0 1. 准 周 2. 3. 1 4. 5. o(n) 四、证明题 证明: 因为 =:::7 " , Z变换的定义有 xc J.. ) ( J.. xC J.. 。z -d z 令走 ::= 11 xc J.. ) == (Z)-k==X(Z) zifT ∞z Kr 五、计算题(每小题 1. t ) == 么F(ω) == 1( 0' 根据频谱搬移特性, 2 =~ x[ =πB(ω--2) 十πB(ω 十2) (3 (4 (3 185

2.解:根据H(x)的定义,x()为因果序列,系统响应为0状态,因此,在方程两边同时进 行Z变换得: aY(z)-bzY(z)=cX(z) (4分) H(x)=Y(z)/X()=c a 4-b21= 、6 (2分) a (2)输入为6(n)时系统的零状态响应的Z变换为 Y(x)=H(x)/X(2x)=ab2[8(n)]=a b (2分) 0 所以,输入为(n)时系统的零状态响应为: y(n)=S.()"u(n) (2分) a 六、作图题(10分) 答案: 品网 2 答图1 (10分) 186
2. 据H( 定义 果 序 方 程 两 Z变换得: a y(z) -bz- 1 y(z) =cX(z) (4 H(z)=¥(z)/X a-oz z c-a (2 b " (2) 为δ 应 的Z c c --z Y(z)=H(z)/X(Z)=~Z[6(n)J= z--αα z- (2 所以,输入为以 )时系统的零状态响应为: y( n U (n) (2 六、作图题 答案: dt. 1 2 3 t -1~ -2 答图 (10 186