
试卷代号:1002 座位号■ 中央广播电视大学2010一2011学年度第二学期“开放本科”期末考试(半开卷) 计算机数学基础(1)试题 2011年7月 题 号 二 三 四 总 分 分 数 得分 评卷人 一、单项选择题(每小题4分,共20分) 1.设P,Q为两个命题,P+Q的真值为0.当且仅当P,Q的赋值为() A.(1,0) B.(0,1) C.(0,0) D.(1,1) 2.设A={1,2},B={a,b,c},C={c,d},则A×(B∩C)=(). A.{,} B.{,} C.{,} D.{,》 3.设A,B,C为三个集合,那么以下推理正确的是(). A.A二B,B二C,则A∈C B.A∈B,B∈C,则A∈C C.A二B,B二C,则A二C D.A∈B,B二C,则A二C 11
试卷代号 0 0 座位号 I I 中央广播电视大学 1学年度第二学期"开放本科"期末考试(半开卷) 计算机数学基础( 1)试题 2011 年7 |题号 - |分数 I I ·1 11 得分|评卷人 一、单项选择题(每小题4分,共 0分) 1. ). A. (1 ,0) B. (0 ,1) c. (0 ,0) D. (1 ,1) 2. == {I , 2},B == {α == ). A. { ,} B. { ,} c. { , } D. { } 3. ). A. ACB ,BcC B. εB ,B εC 则AεC c. ACB ,BcC 则AcC D. Aε 二C 11

4.设图G=,则下列结论成立的是(). A.deg(V)=2E B.deg(V)=E C.∑deg()=2|El EV D.>deg()=E vE y 5.以下命题正确的是(). A.n(n≥l)阶完全图K.都是欧拉图 B.n(n≥1)阶完全图Kn都是哈密顿图 C.n(n≥5)阶完全图K.都是平面图 D.连通且满足m=n一1的图(其中|V|=n,|E|=m)是树 得 分 评卷人 二、填空题(每小题4分,共20分】 6.设Q(x):x是有理数,Z(x):x是整数.则命题“有的有理数是整数”在谓词逻辑中符号 化为 7.设个体域D={1,2},那么谓词公式3xA(x)VHyB(y)消去量词后的等值式为 8.若集合A二⑦当且仅当 017 9.设X={a,b,c},R是X上的二元关系,其关系矩阵为Mk=100,那么R的关系 100 图为 10.设平面图G=有r个面:R。(无限面),R1,R2,…,R,-1,则有2E= 12
4. ). A. deg(V) =2 IE I B. deg(V) = IE I c. ~degω=21£1 vεv D. ~deg(v) = 1£1 5. ). A. n(n 阶完 都是 B. n(n c. n(n 都是 D. l=n,IE I=m.) 得分|评卷入 二、填空题(每小题4分,共 0分) 6. :x 理数 ,Z(x) :x 化为 7. xA(x) V V yB(y) 量 词 8. 集合 且仅 101 其关 ° °1' 100 图为 10. > 有 (元限面) ,孔,凡,…,R川,则有 IE 1= 12
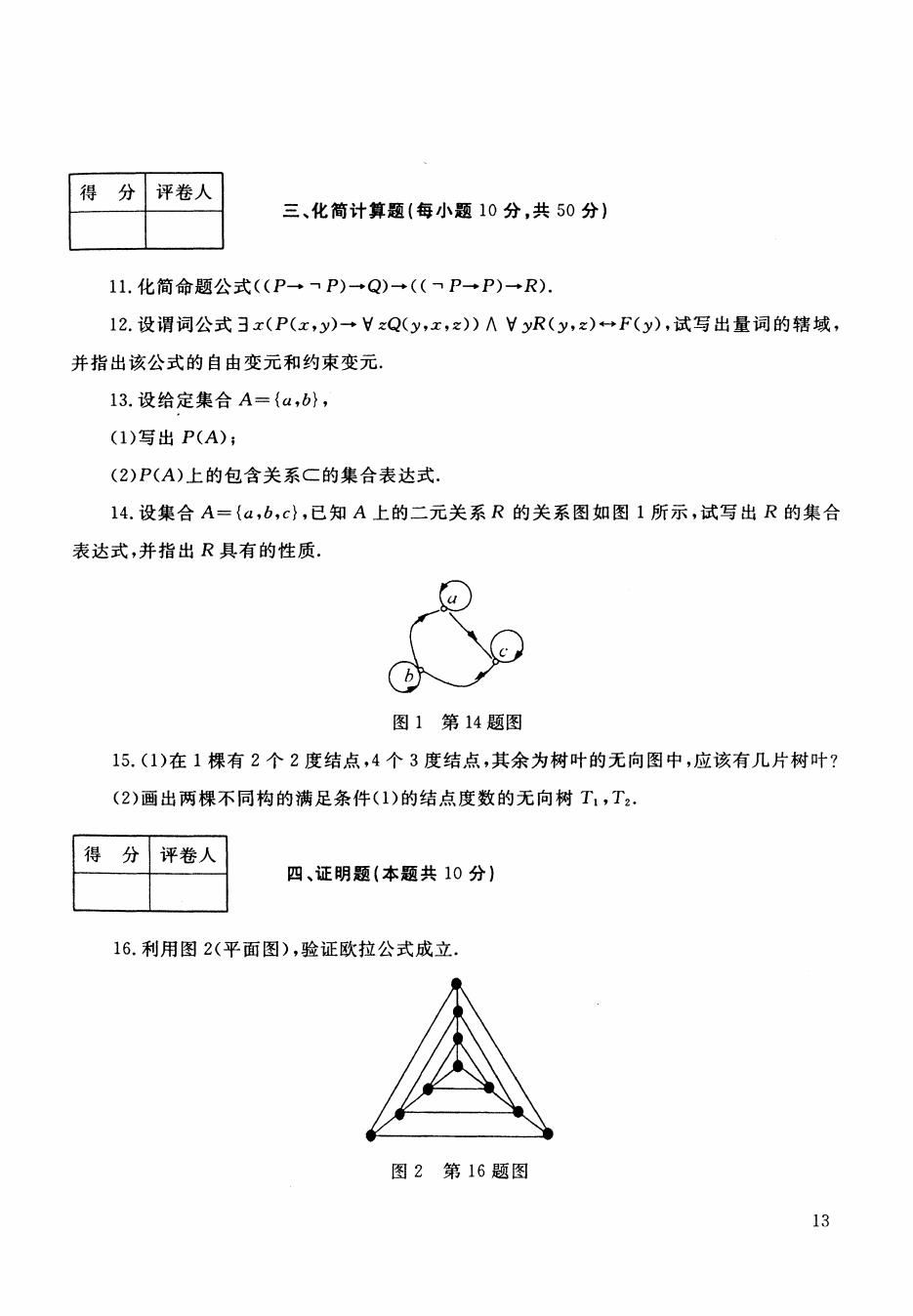
得 分 评卷人 三、化简计算题(每小题10分,共50分) 11.化简命题公式((P→P)+Q)+((P+P)→R), 12.设谓词公式3x(P(x,y)→VxQ(y,x,x))∧HyR(y,z)F(y),试写出量词的辖域, 并指出该公式的自由变元和约束变元 13.设给定集合A={a,b}, (1)写出P(A); (2)P(A)上的包含关系C的集合表达式 14.设集合A={a,b,c},已知A上的二元关系R的关系图如图1所示,试写出R的集合 表达式,并指出R具有的性质. 图1第14题图 15.(1)在1棵有2个2度结点,4个3度结点,其余为树叶的无向图中,应该有几片树叶? (2)画出两棵不同构的满足条件(1)的结点度数的无向树T1,T2. 得 分 评卷人 四、证明题(本题共10分) 16.利用图2(平面图),验证欧拉公式成立. 图2第16题图 13
得分|评卷入 三、化简计算题(每小题 0分,共 0分) 11. ..., P)• Q )• « ..., P•P) • R). 12. zQ(y ,x ,z» 八 V yR(y ,z)• ·F(y) 并指出该公式的自由变元和约束变元. 13. 集合 (1) (2)P(A) 包含 14. 集合 {a b, 表达式,并指出 R具有的性质. 4题图 15. (1) 在1 ,4 (2) 件(1) T 2 • 得分|评卷人 四、证明题(本题共 0分) 16. 图2( ,验证欧拉公式成立. 2第 6题图 13

试卷代号:1002 中央广播电视大学2010一2011学年度第二学期“开放本科”期末考试(半开卷) 计算机数学基础(1)试题答案及评分标准 (供参考) 2011年7月 一、单项选择题(每小题4分,共20分) 1.A 2.B 3.C 4.C 5.D 二、填空题(每小题4分,共20分) 6.3x(Q(z)AZ(x)) 7.A(1)VA(2)V(B(1)AB(2)) 8.A=0 9.如图3所示 图3第9题解图 10. 分deg(R,) 三、化简计算题(每小题10分,共50分) 11.解:((P→P)→+Q)+(PP)→R) 台((PVP)+Q)→((PVP)→R) 台(PVQ)+(PVR) 台(P∧Q)V(PVR) 台((P∧Q)VP)VR 台nPVR (10分) 14
试卷代号 中央广播电视大学 1学年度第二学期"开放本科"期末考试(半开卷) 计算机数学基础。)试题答案及评分标准 (供参考) 2011 年7 一、单项选择题(每小题 1. A 2. B 3. C 4. C 5.D 二、填空题(每小题 2 0 6. 3 x(Q(x) 八Z(x» 7. A (l) V A(2) V (B (l ) 8.A= 9. 图3 9题解图 nu , deUb R 三、化简计算题(每小题 11. «P• -, P)• Q )• « -, p • P )• R ) ∞« -, p V -, P)• Q )• « P V P)• R) -, P V R) 伺( -, -, Q) V ( -, P VR) ∞« -, -, Q) V -, P) VR ∞-, (10 14

12.解:彐x的辖域是:P(x,y)一HzQ(y,x,之); Vz的辖域是:Q(y,x,z); Vy的辖域是:R(y,x) (6分) 公式的自由变元是:P(x,y)→VQ(y,x,之)中的y,R(y,2中的之,F(y)中的y;约束变元 是:P(x,y)→Q(y,x,z)中的x、z,R(y,z)中的y. (10分) 13.解:(1)P(A)={,{a},{b},{a,b}) (4分) (2)c={,,,,} (10分) 14.解:R的表达式为 R={,,,,,} (6分) R具有自反性,反对称性。 (10分) 15.解:(1)设有k片树叶,则该树有k+2+4个结点,根据树的等价定义,有k十5条边.由 握手定理,2×(k+5)=k+2×2+4×3=k+16,故k=6.即有6片树叶. (5分) (2)非同构的树如图4所示 1LiL JLL T T2 图4第14题解图 (10分) 四、证明题(本题共10分) 16.证明:如图2,有r=10个面,v=10个结点,e=18条边. (5分) 即v-e+r=10-18+10=2 所以,欧拉公式成立. (10分) 15
12. 3 eX的辖域是 zQ(y , x ,z); Vz ; Vy 域是 (6 公式的自由变元是 zQ(y ,z) 的y ,R(y ,z) 的z ,F(y) 的y; ~: P(x , y )• V zQ(y ,z) ,z ,R(y ,z) 的y. (10 13. } } (4 (2)C={ , ,, , , } (6 (10 15. (1) 走+2+4 走+5 握手定理, (走十 =走十 =走 6,故走 .即有 6片树叶. (5 (2) 图4 T1 T2 四、证明题(本题共 0分) 16. 图2 ,υ=10 条边 (5 10-18+10=2 所以,欧拉公式成立. (10 15