
第七章无穷级数第二节常数项级数的审敛法人民邮电出版社RISSAHTOTRES
第二节 常数项级数的审敛法 第七章 无穷级数

本节内容正项级数及其审敛法0102交错级数及其审敛法03绝对收敛和条件收敛
本节内容 01 正项级数及其审敛法 02 交错级数及其审敛法 03 绝对收敛和条件收敛

7.2.1正项级数及其审敛法人民邮电出版社RISS&HOTRES
7.2.1 正项级数及其审敛法

内容正项级数0102正项级数审敛法
内容 01 正项级数 02 正项级数审敛法
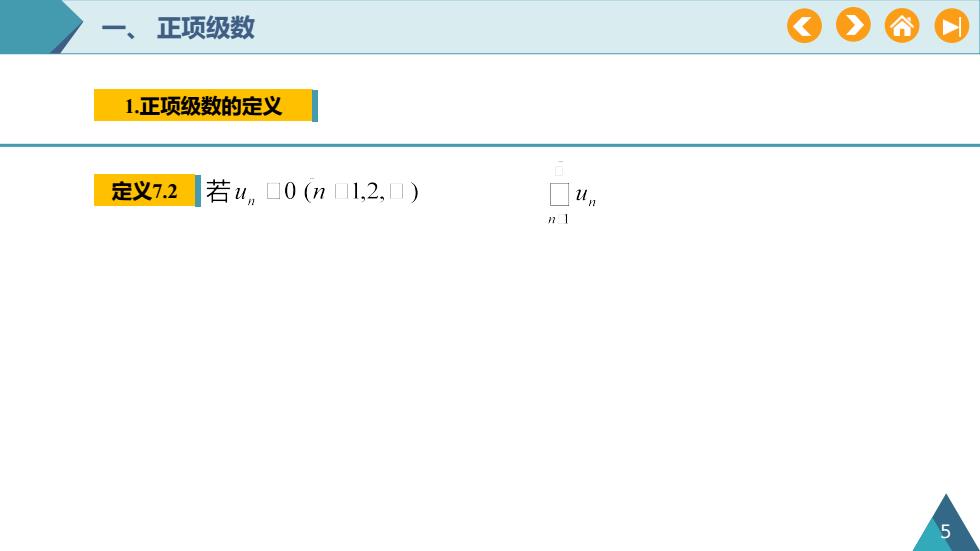
V正项级数1.正项级数的定义定义7.2若uo(n1,2,)n
一、 正项级数 1.正项级数的定义 定义7.2 5
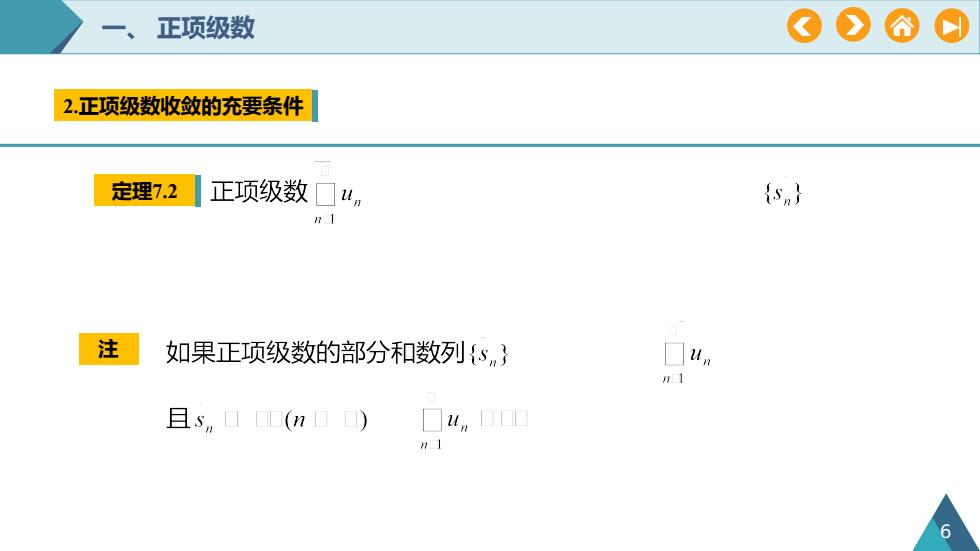
?正项级数P2.正项级数收敛的充要条件定理7.2正项级数u,isnn1注如果正项级数的部分和数列(s,um且s(n)DOLuRI
一、 正项级数 2.正项级数收敛的充要条件 定理7.2 注 6

本讲内容正项级数0102正项级数审敛法1.比较审敛法2.比值审敛法3.根植审敛法
02 本讲内容 01 正项级数 正项级数审敛法 1.比较审敛法 2.比值审敛法 3.根植审敛法

OOA正项级数审敛法1.比较审敛法定理7.3比较审敛法)设uu,y, (n 1,2,)Vn(1)若级数un1n(2)若级数uVn1n注(1)"大收小亦收,小散大亦散";N(2)条件"unv(nl,2,)tkvk使当nN8
二、 正项级数审敛法 1.比较审敛法 定理7.3 注 8

O?7正项级数审敛法111级数p2P3pnpnpn试讨论其敛散性,其中常数p0解当p1福nin当oplpn/nnniS
一、 正项级数审敛法 例 1 解 9

OA正项级数审敛法级数p3p2phph试讨论其敛散性,其中常数p0当pl解1-因此对任意0xn中np11即drnhpn1r111a2p3phbp-1p-部分和数列有界,所以收敛
一、 正项级数审敛法 例 1 解 10