
第九章多元函数微分学及其应用9.4多元函数的极值人民邮电出版社RISS&HOTRES
9.4 多元函数的极值 第九章 多元函数微分学及其应用

本节内容01多元函数的极值02多元函数的最值03条件极值
本节内容 01 多元函数的极值 02 多元函数的最值 03 条件极值
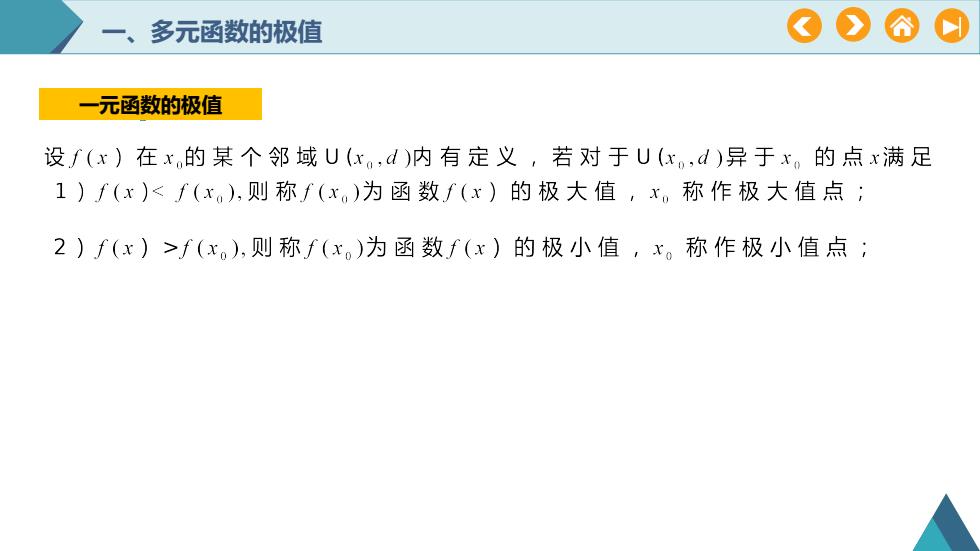
>一、多元函数的极值一元函数的极值设f(x)在x.的某个邻域U(xd)内有定义,若对于U(xd)异于x。的点x满足1)f(x)f(x.)则称f(x)为函数f(x)的极小值,x。称作极小值点
一元函数的极值 一、多元函数的极值

O#0一、多元函数的极值引例Y21在点(0.0)的某邻域内函数值的变化(1)观察函数zC4(2)观察函数z=4-x2-y2在点(0.0)的某邻域内函数值的变化分析1)中,在点(0.0)的某邻域内异于(0.0)的点(x.y),有z(x, y) > z(0, 0) = 0,(2)中,在点(0,0)的某邻域内异于(0,0)的点(x),有z(x, y) <z(0, 0) = 4
引例 分析 一、多元函数的极值 z x O y z x y + = 4 9 2 2 = −x −y 2 2 z 4 z 4 x O y

M一、多元函数的极值定义9.7设函数z=f(x,y)的定义域为DiR2,P(xoy)为D的内点.若存在P(xo,yo)的某个邻域U(P)iD,对于该邻域内异于P(xo,y。)的任意点(x,y),都有f (x, y) f (xo, J))则称函数f(x,y)在点P(xo,J。)有极大值(或极小值)f(x,y),点P(xo,)称为函数f(x,J))的极大值点(或极小值点)极大值与极小值统称为函数的极值,使函数取得极值的点称为函数的极值点:以上关于二元函数的极值的概念,可推广到n元函数
定义9.7 一、多元函数的极值

OOA0一、多元函数的极值设n元函数的定义域为DiR”,P为D的内点.若存在P的某个邻域定义9.8U(P)iD,对于该邻域内异于P的任意点P,都有f(P) f(P)则称函数f(P)在点P有极大值(或极小值)f(P)类似于一元函数取极值的必要条件,我们可以得到类似的二元函数取极值的必要条件如下:定理9.11设函数z=f(x,y)在点(x.y。)处的两个一阶偏导数都存在,若(xo,y)是f(x,y)的极值点,则有f, (xo, J)=0, f, (xo, y)= 0
定义9.8 定理9.11 一、多元函数的极值

OAA一、多元函数的极值证明若(xo,)是f(x,y)的极值点,固定变量y=Jo,所得一元函数f(x,y)在(xo,y)处同样取得极值:由一元函数极值存在的必要条件可得df(x, yo)= 0dx即f(xo,y。)=0,同样可证f(xo.)=0我们把偏导数都等于零的点(xJ)称为函数z=f(x,y)的驻点定理9.11表明,偏导数存在的函数的极值点一定是驻点,但驻点未必是极值点如z=xy,点(O,0)是它的驻点,但不是它的极值点
证明 一、多元函数的极值

OO#0一、多元函数的极值定理9.12设函数z=f(x,J)在点(x:)处的某邻域内具有连续的二阶偏导数,且f.(xo,)=0, f(xo,y)=0, 记A= f(xo,yo), B= fru(xo.yo), C= fu,(xo,o)则有()如果B2-AC0时,f(xo,yo)为极小值,当A0,则f(x,y)在点(xo,)不取极值(3)如果B2-AC=0,则(x,J)在点(xo,y)可能取得极值,也可能不取极值
一、多元函数的极值 定理9.12

CAA一、多元函数的极值求函数极值的步骤如下:=0(1)计算函数z=f(x,J)的偏导数f,f,解方程组求得驻点(xoy)Y,=0.(2)计算所有二阶偏导数,在每一个驻点(xo.y%)处,记A = fr (xo, yo), B= fu(xo, yo),C = f(xo, yo)利用极值存在的充分条件判断其是否为极值点;(3)计算函数的极值
一、多元函数的极值

O?一、多元函数的极值求f(x,)=3-x2+6x-12+5的极值例
例 一、多元函数的极值