
本讲内容7.2.2交错级数及其审敛法7.2.3绝对收敛和条件收敛
本讲内容 7.2.2 交错级数及其审敛法 7.2.3 绝对收敛和条件收敛

?-7.2.2、交错级数及其审敛法1.交错级数的定义定义7.3数项级数Z(-1)-lu, = u, - u, + u, - u + +(-1)"- u, + .n=1Z(-1)"u, = -u +u, -u, +uy -.+(-1)"u, +...n=l其中u,>0(n=1,2,),称为交错级数
7.2.2、 交错级数及其审敛法 1.交错级数的定义 定义7.3 数项级数 1 1 1 2 3 4 1 ( 1) ( 1) n n n n n u u u u u u 2 1 2 3 4 1 ( 1) ( 1) n n n n n u u u u u u
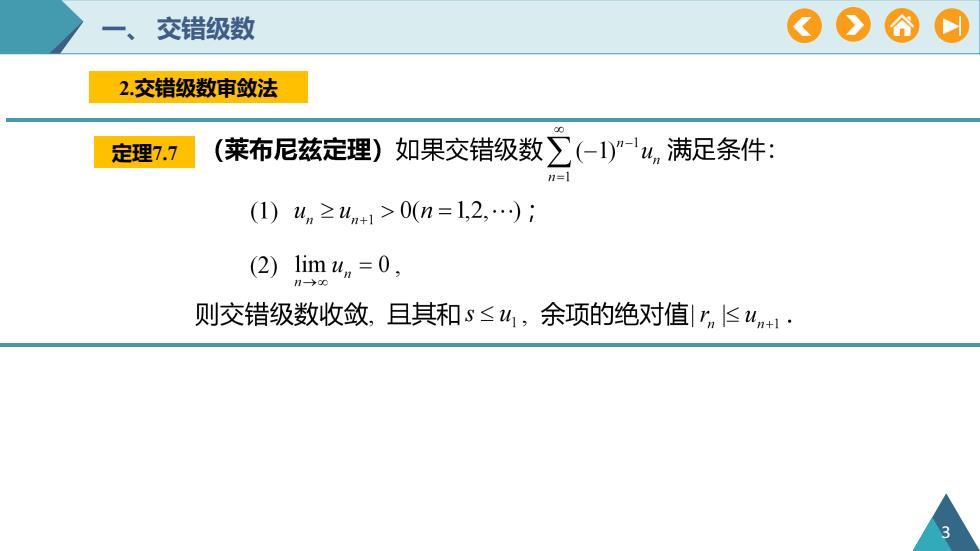
#A交错级数2.交错级数审敛法(莱布尼兹定理)如果交错级数》(-1)"-"u,满足条件:定理7.7n=1(1) u, ≥un+i >0(n=1,2,...) ;lim un = 0,(2)2则交错级数收敛,且其和s≤u,余项的绝对值|r,un+1:
一、 交错级数 2.交错级数审敛法 定理7.7 3
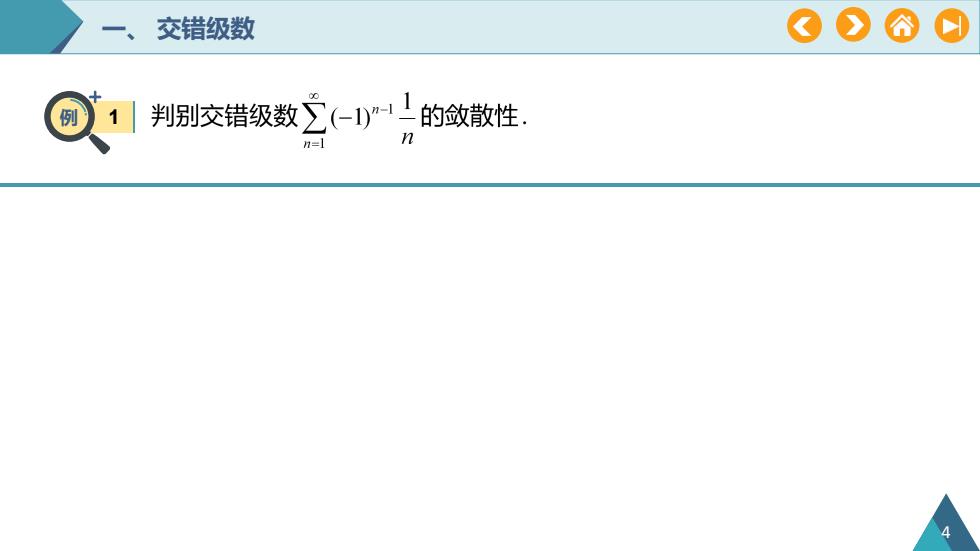
OA交错级数之(-1)"-1}的敛散性.判别交错级数9nn=l
一、 交错级数 例 1 4
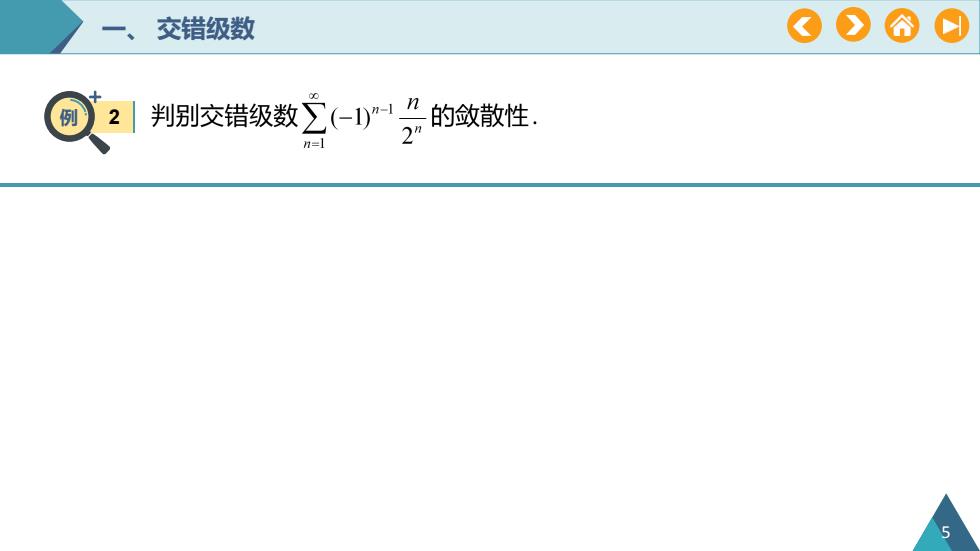
OA交错级数OC(-1)"-1 n的敛散性,判别交错级数>例2nn=lL
一、 交错级数 例 2 5

A交错级数5(-1)"-1 _n同步习题7.2P18的敛散性判别交错级数>3n-l基础题5(2)n=1F
P18 同步习题7.2 基础题5(2) 一、 交错级数 例 3 6
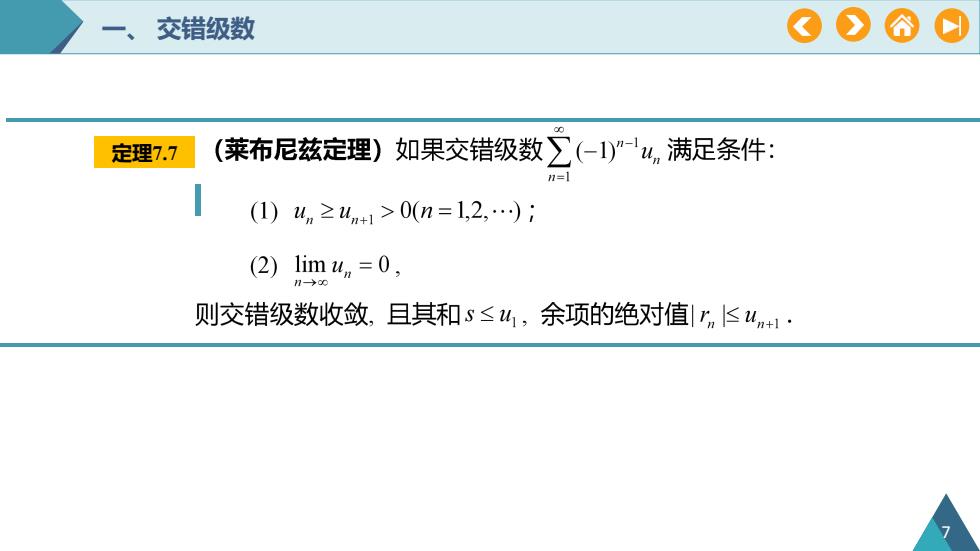
#A交错级数(莱布尼兹定理)如果交错级数》(-1)"-"u,满足条件:定理7.7n=11(1) u, ≥un+i >0(n=1,2,...) ;lim un = 0,(2)2则交错级数收敛,且其和s≤ui,余项的绝对值|r,un+1
一、 交错级数 定理7.7 7

OA交错级数莱布尼兹定理是收敛的充分非必要条件注11例如,级数1+是收敛的423322(2n)3(2n -1)3但其(u,)并不具有单调递减性X
一、 交错级数 注 8 莱布尼兹定理是收敛的充分非必要条件

本讲内容7.2.2交错级数及其审敛法7.2.3绝对收敛和条件收敛
本讲内容 7.2.2 交错级数及其审敛法 7.2.3 绝对收敛和条件收敛

OO607.2.3、纟绝对收敛和条件收敛1.绝对收敛和条件收敛的定义任意项级数:常数项级数un,其中u,(n=1,2,…)是任意实数n=1定义7.4如果级数》u,各项的绝对值所构成的正项级数u,收敛n=ln=女u,绝对收敛;则称级数n=1o0u,收敛,而级数lu,|发散,则称级数u,条件收敛如果级数n=]n=1n=10
7.2.3、 绝对收敛和条件收敛 1.绝对收敛和条件收敛的定义 定义7.4 10