
第7章应用程序设计 内容提要: ■7.1定标与溢出处理 ■7.2基础算术运算 ■7.3FIR滤波器 ■7.4IIR滤波器 ■7.5快速傅里叶变换(FFT) ■7.6 DSPLIB的使用 习题 3
第7章 应用程序设计 内容提要: ◼ 7.1 定标与溢出处理 ◼ 7.2 基础算术运算 ◼ 7.3 FIR滤波器 ◼ 7.4 IIR滤波器 ◼ 7.5 快速傅里叶变换(FFT) ◼ 7.6 DSPLIB的使用 习题 3

7.1 定标与溢出处理 ■7.1.1数的定标 ■7.1.2溢出的处理方法 ■7.1.3常用信号处理算法中的定标方法 4
7.1 定标与溢出处理 ◼ 7.1.1 数的定标 ◼ 7.1.2 溢出的处理方法 ◼ 7.1.3 常用信号处理算法中的定标方法 4

7.1.1数的定标 数的定标: 对C55x而言,参与数值运算的数是16位的整型数。 但数学运算过程中的数不一定都是整数。那么,DSP 芯片是如何处理小数的呢? 这其中的关键就是由程序员来确定一个数的小数点 处于16位中的哪一位,这就是数的定标。 ◆通过设定一个16位数的小数点处于该数中的哪一 位,可以表示不同大小和不同精度的小数。 5
7.1.1 数的定标 ⚫数的定标: 对C55x而言,参与数值运算的数是16位的整型数。 但数学运算过程中的数不一定都是整数。那么,DSP 芯片是如何处理小数的呢? 这其中的关键就是由程序员来确定一个数的小数点 处于16位中的哪一位,这就是数的定标。 ◆通过设定一个16位数的小数点处于该数中的哪一 位,可以表示不同大小和不同精度的小数。 5

7.1.1数的定标 1.小数定点数的定标(scale) 计算机有两种数据表示方法:3 130 2322 0 >浮点数表示法 阶码E 尾数M 32位浮点数真值:x=仁1)×(1.M)×2(B-12 >定点数表示法 二进制小数 定点数就是小数点位置固定的数。数据的表示形式是: 符号位(1位)整数部分(m位).小数部分(n位) C55xDSP是定点芯片,采用补码形式来表示无符号 数和有符号数。 6
1.小数定点数的定标(scale) 计算机有两种数据表示方法: ➢浮点数表示法 ➢定点数表示法 定点数就是小数点位置固定的数。数据的表示形式是: 6 7.1.1 数的定标 C55x DSP是定点芯片,采用补码形式来表示无符号 数和有符号数。 S 阶码E 尾数 M 31 30 23 22 0 32位浮点数真值: x = (-1) s (1.M) 2 (E-127) 二进制小数 符号位(1位)整数部分(m位).小数部分(n位)

7.1.1数的定标 2.数的定标主要采用Q表示法 CPU在执行指令时,并不知道处理的数据是整数 还是小数,也不能指出小数点的位置。在编程时必 须由程序员指出一个数的小数点处于哪一位,这就 是定标(scale)的概念。 常用的定标方法是Q表示法,Q表示法用Q0,Q1,… Qi,Q15分别表示小数点在D0位之后、D1位之 后、.Di位之后、.D15位之后。 严格地,是Qm.n格式:n位小数,m位整数,1位符 号位,共m+n+1位二进制数。也称S表示法Sm.n 符号位(1位)整数部分(m位).小数部分(n位) 7
2.数的定标主要采用Q表示法 CPU在执行指令时,并不知道处理的数据是整数 还是小数,也不能指出小数点的位置。在编程时必 须由程序员指出一个数的小数点处于哪一位,这就 是定标(scale)的概念。 常用的定标方法是Q表示法, Q表示法用Q0, Q1,… Qi, …, Q15 分别表示小数点在D0位之后、D1位之 后、…Di位之后、…D15位之后。 7 7.1.1 数的定标 严格地, 是Qm.n 格式: n位小数, m位整数, 1位符 号位, 共m+n+1位二进制数。 也称S表示法Sm.n 符号位(1位)整数部分(m位).小数部分(n位)
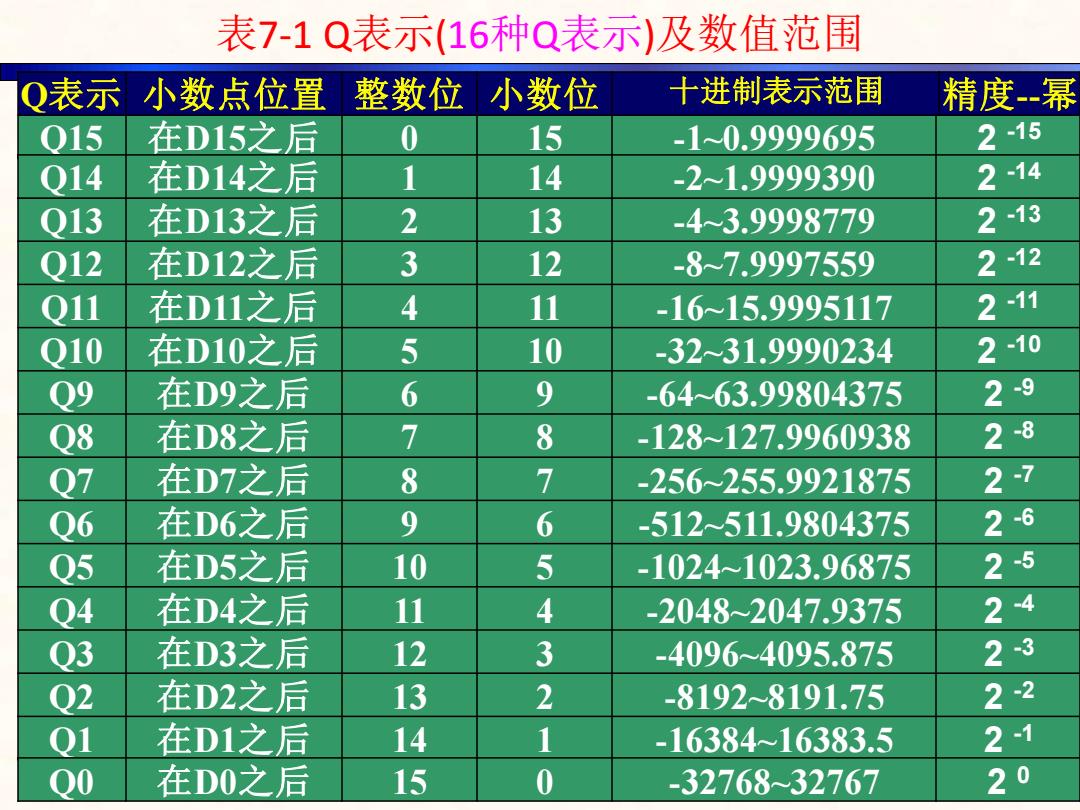
表7-1Q表示(16种Q表示)及数值范围 Q表示小数点位置整数位小数位 十进制表示范围 精度幂 015 在D15之后 0 15 -10.9999695 2-15 Q14 在D14之后 1 14 -2≈1.9999390 2-14 Q13 在D13之后 2 13 -43.9998779 2-13 012 在D12之后 3 12 -8~7.9997559 2-12 011 在D11之后 4 11 -16~15.9995117 2-11 010 在D10之后 5 10 -3231.9990234 2-10 Q9 在D9之后 6 9 -6463.99804375 2-9 Q8 在D8之后 7 8 -128~127.9960938 28 Q7 在D7之后 8 7 -256-255.9921875 2-7 Q6 在D6之后 9 6 -512~511.9804375 2-6 Q5 在D5之后 10 5 -1024~1023.96875 2-5 Q4 在D4之后 11 4 -20482047.9375 24 Q3 在D3之后 12 3 -40964095.875 23 Q2 在D2之后 13 2 -8192~8191.75 22 Q1 在D1之后 14 1 -1638416383.5 2-1 Q0 在D0之后 15 0 -32768-32767 20
Q表示 小数点位置 整数位 小数位 十进制表示范围 精度--幂 Q15 在D15之后 0 15 -1~0.9999695 2 -15 8 Q13 在D13之后 2 13 -4~3.9998779 2 -13 Q12 在D12之后 3 12 -8~7.9997559 2 -12 Q11 在D11之后 4 11 -16~15.9995117 2 -11 Q10 在D10之后 5 10 -32~31.9990234 2 -10 Q9 在D9之后 6 9 -64~63.99804375 2 -9 Q8 在D8之后 7 8 -128~127.9960938 2 -8 Q7 在D7之后 8 7 -256~255.9921875 2 -7 Q6 在D6之后 9 6 -512~511.9804375 2 -6 Q5 在D5之后 10 5 -1024~1023.96875 2 -5 Q4 在D4之后 11 4 -2048~2047.9375 2 -4 Q3 在D3之后 12 3 -4096~4095.875 2 -3 Q2 在D2之后 13 2 -8192~8191.75 2 -2 Q1 在D1之后 14 1 -16384~16383.5 2 -1 Q0 在D0之后 15 0 -32768~32767 2 0 Q14 在D14之后 1 14 -2~1.9999390 2 -14 表7-1 Q表示(16种Q表示)及数值范围

●不同Q值所表示的数不仅范围不同,而且精度也不相同: ◆Q值越大,数值范围越小,但精度越高; ◆Q值越小,数值范围越大,但精度就越低; 例如:Q0数值范围是-32768到+32767,其精度为1; Q15的数值范围为-1到0.9999695,精度为 2-15=1/32768=0.00003051 对定点数而言,数值范围与精度是一对矛盾。一个变量 要想能够表示比较大的数值范围,必须以牺牲精度为代 价:而想提高精度,则数的表示范围就相应地减小。 在实际的定点算法中,应该根据具体问题进行折衷处 理,以达到最佳效果。 9
⚫不同Q值所表示的数不仅范围不同, 而且精度也不相同: ◆ Q值越大, 数值范围越小, 但精度越高; ◆ Q值越小, 数值范围越大,但精度就越低; 例如: Q0数值范围是-32768到+32767,其精度为1; Q15的数值范围为-1到0.9999695, 精度为 2 -15=1/32768 = 0.00003051 ➢对定点数而言, 数值范围与精度是一对矛盾。一个变量 要想能够表示比较大的数值范围, 必须以牺牲精度为代 价; 而想提高精度, 则数的表示范围就相应地减小。 ➢在实际的定点算法中,应该根据具体问题进行折衷处 理, 以达到最佳效果。 9

。在C55x中,16位整数采用补码形式表示。每个采用Qi定标的 16位数用1个符号位、i个小数位和15-i个整数位来表示。 Q15格式小数位权值 LSB MSB(最高位) (最低位) b15 b14 b13 b12 b1 bo -20=一1 ·1/2 1/4 1/8 2-14 2-15 =21 =2-2 =2-3 Q14格式小数位权值 LSB MSB(最高位) (最低位) b15 b14 b13 b12 ●●● b1 bo -2=-21=20· 1/2 1/4 2-13 2-14 Q0格式各位权值 LSB MSB(最高位) (最低位) b15 b14 b13 b12 b1 bo -215 214 213 212 21 20 10
b14 b13 b12 b1 b0 -1 1/2 1/4 1/8 2 -14 2 -15 MSB(最高位) LSB (最低位) Q15格式小数位权值 b15 ⚫在C55x中, 16位整数采用补码形式表示。每个采用Qi定标的 16位数用1个符号位、i个小数位和15-i个整数位来表示。 10 b14 b13 b12 b1 b0 -2 15 2 14 2 13 2 12 2 1 2 0 MSB(最高位) Q0格式各位权值 b15 LSB (最低位) b14 b13 b12 b1 b0 -2 1 1/2 1/4 2 -13 2 -14 MSB(最高位) Q14格式小数位权值 b15 LSB (最低位) . . . =2-1 -2 0= -2 1= =20 =2-2 =2-3
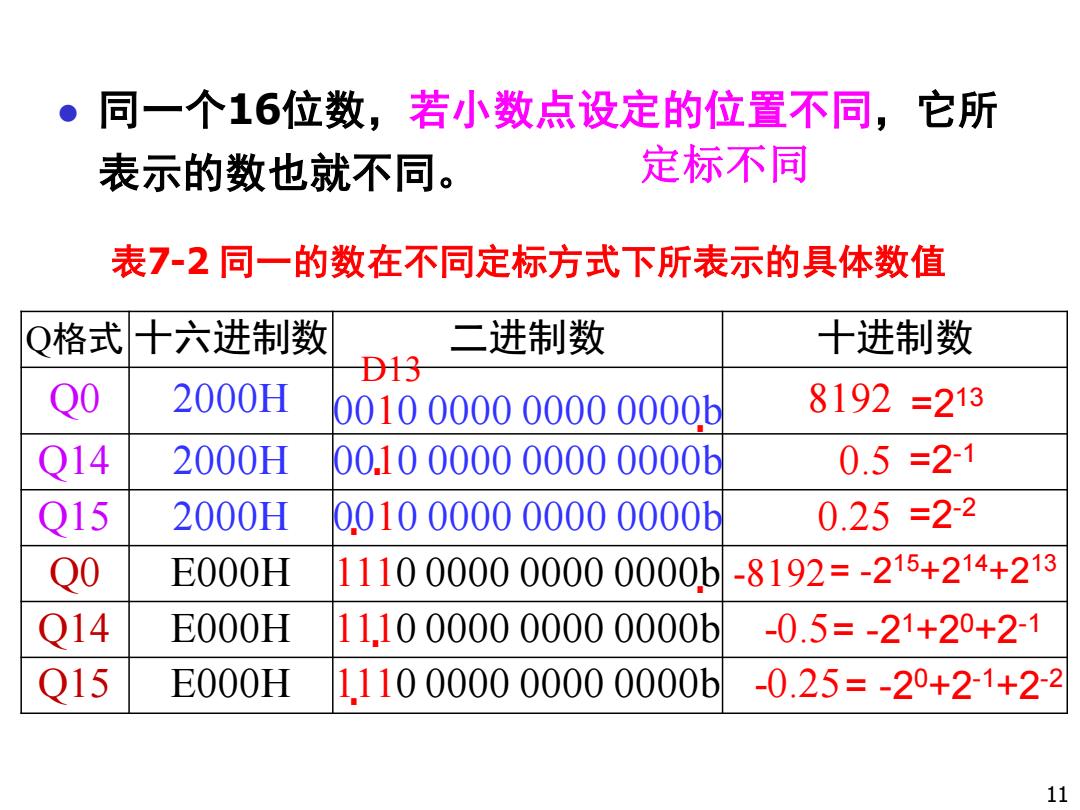
。同一个16位数,若小数点设定的位置不同,它所 表示的数也就不同。 定标不同 表7-2同一的数在不同定标方式下所表示的具体数值 Q格式十六进制数 二进制数 十进制数 D13 Q0 2000H 0010000000000000b 8192=213 Q14 2000H 0010000000000000b 0.5=21 Q15 2000H 0010000000000000b 0.25=22 Q0 E000H 1110000000000000b -8192=-215+214+213 Q14 E000H 11,10000000000000b -0.5=-21+20+21 Q15 E000H 1,110000000000000b -0.25=-20+21+22 11
表7-2 同一的数在不同定标方式下所表示的具体数值 ⚫ 同一个16位数,若小数点设定的位置不同,它所 表示的数也就不同。 Q格式 十六进制数 二进制数 十进制数 Q0 2000H 0010 0000 0000 0000b 8192 Q14 2000H 0010 0000 0000 0000b 0.5 Q15 2000H 0010 0000 0000 0000b 0.25 Q0 E000H 1110 0000 0000 0000b -8192 Q14 E000H 1110 0000 0000 0000b -0.5 Q15 E000H 1110 0000 0000 0000b -0.25 11 定标不同 . . . . . . =213 =2-1 =2-2 = -2 15+214+213 = -2 1+20+2-1 D13 = -2 0+2-1+2-2

7.1 定标与溢出处理 ■7.1.1数的定标 ■7.1.2溢出的处理方法 ■7.1.3常用信号处理算法中的定标方法 TMS320C55x DSP Programmer's Guide Preliminary Draft (SPRU376A.2001) 5.5 Methods of Handling Overflows 12
7.1 定标与溢出处理 ◼ 7.1.1 数的定标 ◼ 7.1.2 溢出的处理方法 ◼ 7.1.3 常用信号处理算法中的定标方法 12 5.5 Methods of Handling Overflows TMS320C55x DSP Programmer’s Guide Preliminary Draft (SPRU376A, 2001年)