
目录 《高等数学A》课程教学大纲. 《线性代数》课程教学大纲 13 《概率论与数理统计》课程教学大纲 ..20 《C语言程序设计》课程教学大纲. .29 《数据结构》课程教学大纲, 41 《离散数学》课程教学大纲 .52 《计算机导论》课程教学大纲, .64 《电路基础》课程教学大纲 ..70 《电路基础》实验教学大纲 ...74 《数字逻辑》课程教学大纲! .76 《数字逻辑》实验教学大纲 .79 《计算机网络》课程教学大纲 81 《计算机组成原理》课程教学大纲 93 《面向对象程序设计》课程教学大纲. .103 《操作系统》课程教学大纲… 110 《数据库原理》课程教学大纲. .121 《编译原理》课程教学大纲, 129 《Java程序设计》课程教学大纲. .139 《Java程序设计》实验教学大纲. 143 《软件工程》课程教学大纲 .146 《算法设计与分析》课程教学大纲 .151 《算法设计与分析》实验教学大纲: 155 《程序设计专题训练》课程教学大纲 158 《软件技术专题训练》课程教学大纲 .162 《云平台环境及虚拟化技术》课程教学大纲 166 《云基础架构与与云安全技术》课程教学大纲 .170 《Web应用技术》课程教学大纲 .173 《软件项目专题训练》课程教学大纲 .177
目 录 《高等数学 A》课程教学大纲..............................................................................................................................1 《线性代数》课程教学大纲...............................................................................................................................13 《概率论与数理统计》课程教学大纲...............................................................................................................20 《C 语言程序设计》课程教学大纲....................................................................................................................29 《数据结构》课程教学大纲...............................................................................................................................41 《离散数学》课程教学大纲...............................................................................................................................52 《计算机导论》课程教学大纲...........................................................................................................................64 《电路基础》课程教学大纲...............................................................................................................................70 《电路基础》实验教学大纲...............................................................................................................................74 《数字逻辑》课程教学大纲...............................................................................................................................76 《数字逻辑》实验教学大纲...............................................................................................................................79 《计算机网络》课程教学大纲...........................................................................................................................81 《计算机组成原理》课程教学大纲...................................................................................................................93 《面向对象程序设计》课程教学大纲.............................................................................................................103 《操作系统》课程教学大纲.............................................................................................................................110 《数据库原理》课程教学大纲.........................................................................................................................121 《编译原理》课程教学大纲.............................................................................................................................129 《Java 程序设计》课程教学大纲....................................................................................................................139 《Java 程序设计》实验教学大纲...................................................................................................................143 《软件工程》课程教学大纲.............................................................................................................................146 《算法设计与分析》课程教学大纲.................................................................................................................151 《算法设计与分析》实验教学大纲.................................................................................................................155 《程序设计专题训练》课程教学大纲.............................................................................................................158 《软件技术专题训练》课程教学大纲.............................................................................................................162 《云平台环境及虚拟化技术》课程教学大纲.................................................................................................166 《云基础架构与与云安全技术》课程教学大纲.............................................................................................170 《Web 应用技术》课程教学大纲......................................................................................................................173 《软件项目专题训练》课程教学大纲.............................................................................................................177

《微机原理与接口技术》课程教学大纲 .180 《计算机网络安全》课程教学大纲 184 《人工智能》课程教学大纲.… 187 《计算机图形学》课程教学大纲。 .191 《多媒体技术及应用》课程教学大纲 195 《Windows软件开发技术》课程教学大纲. .198 《数据挖掘》课程教学大纲. 203 《数学建模》课程教学大纲.… .206 《Linux操作系统》课程教学大纲. .209 《Unix/几inux系统编程》课程教学大纲. 213 《网络数据库技术》课程教学大纲」 217 《专业英语》课程教学大纲… .223 《Python语言程序设计》课程教学大纲. 226 《计算机新技术讲座》课程教学大纲 231 《平面设计与动画设计》课程教学大纲 .233 《大数据分析与处理技术》课程教学大纲. .243 《课件及微课制作技术》课程教学大纲… 245 《信息学奥赛》课程教学大纲. 248 《中学信息技术课程标准与教材研究》课程教学大纲 251 《中学信息技术教学设计》课程教学大纲 256 《中学信息技术综合实践活动》课程教学大纲 263
《微机原理与接口技术》课程教学大纲.........................................................................................................180 《计算机网络安全》课程教学大纲.................................................................................................................184 《人工智能》课程教学大纲.............................................................................................................................187 《计算机图形学》课程教学大纲.....................................................................................................................191 《多媒体技术及应用》课程教学大纲.............................................................................................................195 《Windows 软件开发技术》课程教学大纲......................................................................................................198 《数据挖掘》课程教学大纲.............................................................................................................................203 《数学建模》课程教学大纲.............................................................................................................................206 《Linux 操作系统》课程教学大纲..................................................................................................................209 《Unix/Linux 系统编程》课程教学大纲........................................................................................................213 《网络数据库技术》课程教学大纲.................................................................................................................217 《专业英语》课程教学大纲.............................................................................................................................223 《Python 语言程序设计》课程教学大纲........................................................................................................226 《计算机新技术讲座》课程教学大纲.............................................................................................................231 《平面设计与动画设计》课程教学大纲.........................................................................................................233 《大数据分析与处理技术》课程教学大纲.....................................................................................................243 《课件及微课制作技术》课程教学大纲.........................................................................................................245 《信息学奥赛》课程教学大纲.........................................................................................................................248 《中学信息技术课程标准与教材研究》课程教学大纲................................................................................ 251 《中学信息技术教学设计》课程教学大纲.....................................................................................................256 《中学信息技术综合实践活动》课程教学大纲.............................................................................................263

《高等数学A》课程教学大纲 一、课程基本信息 课程 课程 9388001/9388002 高等数学 编号 名称 学分/学时 10学分160学时(4/64,6/96) 开课时间 第1学期(13周)、第2学期(16周) 课程性质 专业基础课 先修课程 《高中数学》 考核方式 考试(平时30%、期末考试70%) 课程基 本情况 课程负责人 教材: 《高等数学》上下册,同济大学数学系编,人民邮电出版社, 2016年。 参考书目: 教材及 ①《高等数学》(第七版),同济大学数学系编,高等教育出版社, 参考书 2004年: ⊙ 《高等数学》上下册,童裕孙等编写,高等教育出版社 ③ 《高等数学》上下册,上海交通大学数学系编,上海交通大学出 版社,2017年 《高等数学》是计算机、电子等理工类专业必修课。本课程主要讲授函数、极限与连续, 课程 一元函数微分学及其应,一元函数积分学及其应用,微分方程,向量与空间解析几何, 简介 多元函数微分学,多元函数积分学,无穷级数。本课程是进一步学习《概率论与概率 统计》等后续课程的基础。 学习目标1:了解高等数学课程的地位与性质,系统掌握高等数学的基本概念、基本 理论和基本方法。 课程学习 学习目标2:培养学生分析问题、解决问题的能力。 目标 学习目标3:为进一步学习《概率统计》等后续课程,打下坚实的基础
《高等数学 A》课程教学大纲 一、课程基本信息 课程 编号 9388001/9388002 课程 名称 高等数学 课 程 基 本 情 况 学分/学时 10 学分/160 学时(4/64,6/96) 开课时间 第 1 学期(13 周)、第 2 学期(16 周) 课程性质 专业基础课 先修课程 《高中数学》 考核方式 考 试(平时 30%、期末考试 70%) 课程负责人 教材及 参考书 教材:《高等数学》上下册,同济大学数学系编,人民邮电出版社, 2016 年。 参考书目: 1 《高等数学》(第七版),同济大学数学系编,高等教育出版社, 2004 年; 2 《高等数学》上下册,童裕孙等编写,高等教育出版社 3 《高等数学》上下册,上海交通大学数学系编,上海交通大学出 版社,2017 年 课 程 简 介 《高等数学》是计算机、电子等理工类专业必修课。本课程主要讲授函数、极限与连续, 一元函数微分学及其应,一元函数积分学及其应用,微分方程,向量与空间解析几何, 多元函数微分学,多元函数积分学,无穷级数。本课程是进一步学习《概率论与概率 统计》等后续课程的基础。 课程学习 目标 学习目标 1:了解高等数学课程的地位与性质,系统掌握高等数学的基本概念、基本 理论和基本方法。 学习目标 2:培养学生分析问题、解决问题的能力。 学习目标 3:为进一步学习《概率统计》等后续课程,打下坚实的基础。 1

二、课程学习目标与毕业要求指标点的对应关系 专业毕业要求 专业毕业要求指标点 对应的课程学习目标 了解本专业的发展概况及其在社会发展中的重要作用,了 解数学教学领域的一些最新研究成果和教学方法:掌握教育 学、心理学和数学教育的基本理论,熟悉中小学教育技术以及 2.3知识整合 教育法规:学习人类文明进步与文化发展的通识知识。具有 课程学习目标1、2、3 整合数学、教育学、心理学等知识和教育技术并进行知识与技 能重构的能力。 具备良好的数学素养,深入理解高等数学并掌握的基本理 论和方法,并能获得较强的逻辑推理能力和抽象思维能力。初 2.4教学能力 步掌握高等数学的基本思想方法,具有分析问题、解决实际问 课程学习目标1、2、3 题等基本能力:具有较强的独立学习能力和创新思维方式,懂 得教育教学基本规律,掌握现代教育教学、心理学的基本理论。 三、课程各要素与课程学习目标的对应关系及达成度分析 (一)课程教学内容、教学目标、学时分配与课程学习目标的对应关系 第一章函数、极限与连续(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握集合及其运算、邻域、基本初等函数及初等函数的基本概念:数列、函数极限的基本概念、 求极限的基本方法及极限的性质及其证明:两个重要极限的应用:无穷大与无穷小的基本概念及其关系、 无穷小阶的比较:函数的连续性及其性质。 2.教学内容 第1.1节:集合与函数 第1.2节:数列极限的定义与计算 第1.3节:函数极限的定义与计算 第1.4节:极限性质 第1.5节:两个重要极限 第1.6节:无穷小与无穷大 第1.7节:函数的连续性及其性质
二、课程学习目标与毕业要求指标点的对应关系 专业毕业要求 专业毕业要求指标点 对应的课程学习目标 2.3 知识整合 了解本专业的发展概况及其在社会发展中的重要作用,了 解数学教学领域的一些最新研究成果和教学方法;掌握教育 学、心理学和数学教育的基本理论,熟悉中小学教育技术以及 教育法规; 学习人类文明进步与文化发展的通识知识。具有 整合数学、教育学、心理学等知识和教育技术并进行知识与技 能重构的能力。 课程学习目标 1、2、3 2.4 教学能力 具备良好的数学素养,深入理解高等数学并掌握的基本理 论和方法,并能获得较强的逻辑推理能力和抽象思维能力。初 步掌握高等数学的基本思想方法,具有分析问题、解决实际问 题等基本能力;具有较强的独立学习能力和创新思维方式,懂 得教育教学基本规律,掌握现代教育教学、心理学的基本理论。 课程学习目标 1、2、3 三、课程各要素与课程学习目标的对应关系及达成度分析 (一)课程教学内容、教学目标、学时分配与课程学习目标的对应关系 第一章 函数、极限与连续(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握集合及其运算、邻域、基本初等函数及初等函数的基本概念;数列、函数极限的基本概念、 求极限的基本方法及极限的性质及其证明;两个重要极限的应用;无穷大与无穷小的基本概念及其关系、 无穷小阶的比较;函数的连续性及其性质。 2 . 教学内容 第 1.1 节:集合与函数 第 1.2 节:数列极限的定义与计算 第 1.3 节:函数极限的定义与计算 第 1.4 节:极限性质 第 1.5 节:两个重要极限 第 1.6 节:无穷小与无穷大 第 1.7 节:函数的连续性及其性质 2

3.重点:数列极限的概念及性质,函数极限的概念与性质,函数极限与数列极限的关系,极限存在准 则两个重要极限和闭区间上连续函数的性质 4.难点:难点是数列极限与函数极限的概念,利用定义证明极限的相关题目。 5.参考习题: 习题1-1:第1(4)、2、3、4题(3、5、6)、6(2、5-8)、9-11、14-15题 习题1-2:第2(2-10)、3-5题 习题1-3:第1(3、5、6、8-14)、2-5题 习题1-4:第1-9题 习题1-5:第1-4题 习题1-6:第2-5题 习题1-7:第1-13题 章节测试题:全部 6.学时:18学时 第二章一元函数微分学及其应用(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握导数的基本概念及基本求导公式:求导数、高阶导数的方法与技巧;掌握微分的基本及微分 的求法:掌握微分中值定理的内容、证明方法及其应用、泰勒中值定理的应用:熟练掌握函数单调性的 判别方法、求函数的单调区间与极值、凹凸区间与拐点,求函数的最值、曲率,并可以解决一些简单的 实际问题 2.教学内容 第2.1节:导数的概念及基本求导公式 第2.2节:导数的计算法则 第2.3节:微分的概念应用 第2.4节:微分中值定理及其应用 第2.5节:泰勒中值定理 第2.6节:函数的性态与图形 第2.7节:微分学的实际应用 3.重点:导数的定义,函数的求导法则及函数的微分,微分中值定理,洛必达法则,泰勒公式,函数的 单调性与凹凸性,函数的极值与最值: 4难点:复合函数的求导法则,反函数及参数方程求高阶导数,微分中值定理及其应用,函数图形的描 绘
3 . 重点:数列极限的概念及性质,函数极限的概念与性质,函数极限与数列极限的关系,极限存在准 则 两个重要极限和闭区间上连续函数的性质 4 . 难点:难点是数列极限与函数极限的概念,利用定义证明极限的相关题目。 5 . 参考习题: 习题 1-1:第 1(4)、2、3、4 题(3、5、6)、6(2、5-8)、9-11、14-15 题 习题 1-2:第 2(2-10)、3-5 题 习题 1-3:第 1(3、5、6、8-14)、2-5 题 习题 1-4:第 1-9 题 习题 1-5:第 1-4 题 习题 1-6:第 2-5 题 习题 1-7:第 1-13 题 章节测试题:全部 6 . 学时:18 学时 第二章 一元函数微分学及其应用(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握导数的基本概念及基本求导公式;求导数、高阶导数的方法与技巧;掌握微分的基本及微分 的求法;掌握微分中值定理的内容、证明方法及其应用、泰勒中值定理的应用;熟练掌握函数单调性的 判别方法、求函数的单调区间与极值、凹凸区间与拐点,求函数的最值、曲率,并可以解决一些简单的 实际问题 2 . 教学内容 第 2.1 节:导数的概念及基本求导公式 第 2.2 节:导数的计算法则 第 2.3 节:微分的概念应用 第 2.4 节:微分中值定理及其应用 第 2.5 节:泰勒中值定理 第 2.6 节:函数的性态与图形 第 2.7 节:微分学的实际应用 3.重点:导数的定义,函数的求导法则及函数的微分, 微分中值定理,洛必达法则,泰勒公式,函数的 单调性与凹凸性,函数的极值与最值; 4.难点:复合函数的求导法则,反函数及参数方程求高阶导数,微分中值定理及其应用,函数图形的描 绘。 3

5.参考习题: 习题2-1:第1题、第3、4、6、8-11题 习题2-2:第1、2、3(5、6、11、13-16)、4(14-18)、5(11-18)、6、7(7-10)、8-19题 习题2-3:第1、5、6、8-10题 习题2-4:第1-10题 习题2-5:第1-4题 习题2-6:第1(4、7、8)、2-7、9-14、16题 习题2-7:第1-25题 章节测试题:全部 6.学时:24学时 第三章一元函数积分学及其应用(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握不定积分的概念与性质,求不定积分的方法与技巧,定积分概念与性质,微积分基本公式,求 定积分的方法与技巧,定积分的应用,反常定积的基本概念及计算。 2.教学内容 第3.1节:不定积分的概念与性质 第3.2节:不定积分的换元法与分部法 第33节:有理函数的不定积分 第3.4节:定积分的概念与性质 第3.5节:微积分基本定理 第3.6节:定积分的换元法与分部法 第3.7节:定积分的几何应用与物理应用 第3.8节:反常积分 3.重点:不定积分的概念与性质,不定积分的换元法与分部积分法,有理函数的积分:定积分的概念与 性质,微积分基本公式,定积分的换元积分与分部积分法:定积分微元法的思想,定积分在几何与物理 学方面的应用。: 4.难点:利用第二换元积分法求不定积分,有理函数的不定积分:利用换元法求定积分:掌握微元法的 思想及微元法的应用。 5.参考习题: 习题3-1:第2(11、13、14、18-26)、3-7题 习题3-2:第2-6题
5 . 参考习题: 习题 2-1:第 1 题、第 3、4、6、8-11 题 习题 2-2:第 1、2、3(5、6、11、13-16)、4(14-18)、5(11-18)、6、7(7-10)、8-19 题 习题 2-3:第 1、5、6、8-10 题 习题 2-4:第 1-10 题 习题 2-5:第 1-4 题 习题 2-6:第 1(4、7、8)、2-7、9-14、16 题 习题 2-7:第 1-25 题 章节测试题:全部 6 . 学时:24 学时 第三章 一元函数积分学及其应用(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握不定积分的概念与性质,求不定积分的方法与技巧,定积分概念与性质,微积分基本公式,求 定积分的方法与技巧,定积分的应用,反常定积的基本概念及计算。 2 . 教学内容 第 3.1 节:不定积分的概念与性质 第 3.2 节:不定积分的换元法与分部法 第 3.3 节:有理函数的不定积分 第 3.4 节:定积分的概念与性质 第 3.5 节:微积分基本定理 第 3.6 节:定积分的换元法与分部法 第 3.7 节:定积分的几何应用与物理应用 第 3.8 节:反常积分 3.重点:不定积分的概念与性质,不定积分的换元法与分部积分法,有理函数的积分;定积分的概念与 性质,微积分基本公式,定积分的换元积分与分部积分法;定积分微元法的思想,定积分在几何与物理 学方面的应用。; 4.难点:利用第二换元积分法求不定积分,有理函数的不定积分;利用换元法求定积分;掌握微元法的 思想及微元法的应用。 5 . 参考习题: 习题 3-1:第 2(11、13、14、18-26)、3-7 题 习题 3-2:第 2-6 题 4

习题3-3:第1-3题 习题3-4:第1(2)、3、3、6-9题 习题3-5:第1-13题 习题3-6:第1-11题 习题3-7:第1-8题 习题3-8:第1-3题 章节测试题:全部 6.学时:22学时 第四章微分方程(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握微分方程的基本概念,可分离变量的微分方程,齐次方程,一阶线性微分方程,可降阶的二阶 微分方程,线性微分方程解的结构,常系数齐次线性微分方程,常系数非齐次线性微分方程。 2.教学内容 第41节:微分方程的概念 第4.2节:一阶微分方程 第4.3节:二阶微分方程 3.重点:一阶线性微分方程,高阶线性微分方程,常系数非齐次线性微分方程: 4.难点:可降阶的高阶微分方程,常系数非齐次线性微分方程中特解的求法。 5.参考习题: 习题4-1:第1、2、5-7题 习题4-2:第1-3、5-8题 习题4-3:第1、4-6、8-9题 章节测试题:1、2、4-6 6.学时:12学时 第五章向量与空间解析几何(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握向量及其线性运算,数量积、向量积混合积,平面及其方程,空间直线及其方程,曲面及其 方程,空间曲线及其方程。 2.教学内容 第5.1节:向量及其运算 第5.2节:平面及其方程
习题 3-3:第 1-3 题 习题 3-4:第 1(2)、3、3、6-9 题 习题 3-5:第 1-13 题 习题 3-6:第 1-11 题 习题 3-7:第 1-8 题 习题 3-8:第 1-3 题 章节测试题:全部 6 . 学时:22 学时 第四章 微分方程(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握微分方程的基本概念,可分离变量的微分方程,齐次方程,一阶线性微分方程,可降阶的二阶 微分方程,线性微分方程解的结构,常系数齐次线性微分方程,常系数非齐次线性微分方程。 2 . 教学内容 第 4.1 节:微分方程的概念 第 4.2 节:一阶微分方程 第 4.3 节:二阶微分方程 3.重点:一阶线性微分方程,高阶线性微分方程,常系数非齐次线性微分方程; 4. 难点:可降阶的高阶微分方程,常系数非齐次线性微分方程中特解的求法。 5 . 参考习题: 习题 4-1:第 1、2、5-7 题 习题 4-2:第 1-3、5-8 题 习题 4-3:第 1、4-6、8-9 题 章节测试题:1、2、4-6 6 . 学时:12 学时 第五章 向量与空间解析几何(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握向量及其线性运算,数量积、向量积 混合积,平面及其方程,空间直线及其方程,曲面及其 方程,空间曲线及其方程。 2 . 教学内容 第 5.1 节:向量及其运算 第 5.2 节:平面及其方程 5

第5.3节:直线及其方程 第5.4节:曲面与曲线 3.重点:向量的数量积,向量积与混合积,曲面及其方程,曲线及其方程,平面及其方程,空间直线及 其方程: 4.难点:曲面及其方程,空间曲线及其方程,空间直线方程的求法。 5.参考习题: 习题5-1:第1-30题 习题5-2:第1、3-16题 习题5-3:第1-21题 习题5-4:第1-17题 章节测试题:全部 6.学时:14学时 第六章多元函数微分学(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握二元函数的概念、极限与连续,偏导数,全微分,多元复合函数的求导法则,隐函数的求导公 式,多元函数微分学的几何应用,方向导数与梯度,多元函数的极值及其求法。 2.教学内容 第6.1节:多元函数的概念、极限与连续 第62节:多元函数的偏导数与全微分 第6.3节:复合求导、隐函数的求导及方向导数 第6.4节:多元函数微分学的应用 3.重点:多元函数的偏导数,全微分,复合函数的求导法则,隐函数的求导公式,多元函数微分学在 几何方面的应用,多元函数的极值及其求法: 4.难点:复合函数的高阶导数求法,隐函数的求导公式的推导,多元函数的极值及求法。 5.参考习题: 习题6-1:第1-6题 习题6-2:第1-14题 习题6-3:第1-40题 习题6-4:第1-25题 章节测试题:全部 6.学时:20学时 6
第 5.3 节:直线及其方程 第 5.4 节:曲面与曲线 3.重点:向量的数量积,向量积与混合积,曲面及其方程,曲线及其方程,平面及其方程,空间直线及 其方程; 4.难点:曲面及其方程,空间曲线及其方程,空间直线方程的求法。 5 . 参考习题: 习题 5-1:第 1-30 题 习题 5-2:第 1、3-16 题 习题 5-3:第 1-21 题 习题 5-4:第 1-17 题 章节测试题:全部 6 . 学时:14 学时 第六章 多元函数微分学(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握二元函数的概念、极限与连续,偏导数,全微分,多元复合函数的求导法则,隐函数的求导公 式,多元函数微分学的几何应用,方向导数与梯度,多元函数的极值及其求法。 2 . 教学内容 第 6.1 节:多元函数的概念、极限与连续 第 6.2 节:多元函数的偏导数与全微分 第 6.3 节:复合求导、隐函数的求导及方向导数 第 6.4 节:多元函数微分学的应用 3.重点:多元函数的偏导数,全微分,复合函数的求导法则,隐函数的求导公式,多元函数微分学在 几何方面的应用,多元函数的极值及其求法; 4. 难点:复合函数的高阶导数求法,隐函数的求导公式的推导,多元函数的极值及求法。 5 . 参考习题: 习题 6-1:第 1-6 题 习题 6-2:第 1-14 题 习题 6-3:第 1-40 题 习题 6-4:第 1-25 题 章节测试题:全部 6 . 学时:20 学时 6

第七章多元函数积分学(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握二重积分的概念与性质,二重积分的计算法及应用,三重积分概念、计算和应用:对弧长的曲 线积分,对坐标的曲线积分,对面积的曲面积分,对坐标的曲面积分:格林公式及其应用,高斯公式通 量与散度,斯托克斯公式环流量与旋度。 2.教学内容 第7.1节:二重积分的概念、计算和应用 第7.2节:三重积分的概念、计算和应用 第7.3节:对弧长的曲线积分与对坐标的曲线积分 第7.4节:对面积的曲面积分与对坐标的曲面积分 第7.5节:格林公式、高斯高斯和斯托克斯公式 3.重点:二重积分的概念与性质,二重积分的计算,三重积分的计算,重积分的应用:重点是对弧长的 曲线积分,对坐标的曲线积分,格林公式及其应用,对面积的曲面积分,对坐标的曲面积分,高斯公式, 斯托克斯公式。 4.难点:在极坐标系下计算二重积分,三重积分的计算:对坐标的曲线与曲面积分,格林公式,高斯公 式,斯托克斯公式的条件,证明思想及其应用。 5.参考习题: 习题7-1:第1-31题 习题7-2:第1-13题 习题7-3:第1-13题 习题7-4:第1-8题 习题7-5:第1-16题 章节测试题:全部 6.学时:34学时 第八章无穷级数(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握常数项级数的概念和性质,常数项级数的审敛法,幂级数,函数展开成幂级数,函数的幂级数 展开式的应用,傅里叶级数,一般周期函数的傅里叶级数。 2.教学内容 第8.1节:常数项级数的概念与性质 第82节:常数项级数的审敛准则 第8.3节:幂级数的收敛及函数的展开式 1
第七章 多元函数积分学(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握二重积分的概念与性质,二重积分的计算法及应用,三重积分概念、计算和应用;对弧长的曲 线积分,对坐标的曲线积分,对面积的曲面积分,对坐标的曲面积分;格林公式及其应用,高斯公式 通 量与散度,斯托克斯公式 环流量与旋度。 2 . 教学内容 第 7.1 节:二重积分的概念、计算和应用 第 7.2 节:三重积分的概念、计算和应用 第 7.3 节:对弧长的曲线积分与对坐标的曲线积分 第 7.4 节:对面积的曲面积分与对坐标的曲面积分 第 7.5 节:格林公式、高斯高斯和斯托克斯公式 3.重点:二重积分的概念与性质,二重积分的计算,三重积分的计算,重积分的应用;重点是对弧长的 曲线积分,对坐标的曲线积分,格林公式及其应用,对面积的曲面积分,对坐标的曲面积分,高斯公式, 斯托克斯公式。 4. 难点:在极坐标系下计算二重积分,三重积分的计算;对坐标的曲线与曲面积分,格林公式,高斯公 式,斯托克斯公式的条件,证明思想及其应用。 5 . 参考习题: 习题 7-1:第 1-31 题 习题 7-2:第 1-13 题 习题 7-3:第 1-13 题 习题 7-4:第 1-8 题 习题 7-5:第 1-16 题 章节测试题:全部 6 . 学时:34 学时 第八章 无穷级数(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握常数项级数的概念和性质,常数项级数的审敛法,幂级数,函数展开成幂级数,函数的幂级数 展开式的应用,傅里叶级数,一般周期函数的傅里叶级数。 2 . 教学内容 第 8.1 节:常数项级数的概念与性质 第 8.2 节:常数项级数的审敛准则 第 8.3 节:幂级数的收敛及函数的展开式 7
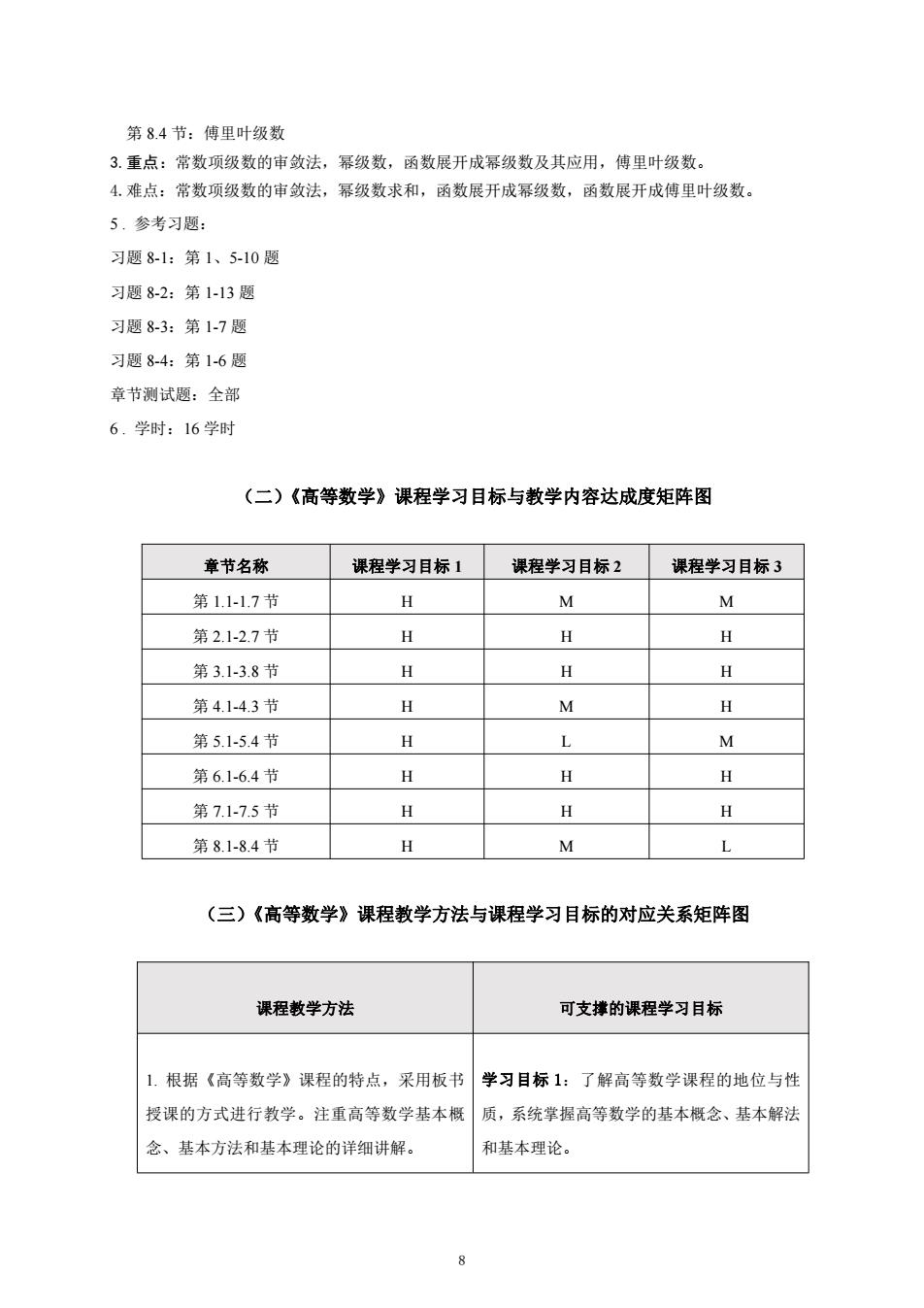
第8.4节:傅里叶级数 3.重点:常数项级数的审敛法,幂级数,函数展开成幂级数及其应用,傅里叶级数。 4.难点:常数项级数的审敛法,幂级数求和,函数展开成幂级数,函数展开成傅里叶级数。 5.参考习题: 习题8-1:第1、5-10题 习题8-2:第1-13题 习题8-3:第1-7题 习题8-4:第1-6题 章节测试题:全部 6.学时:16学时 (二)《高等数学》课程学习目标与教学内容达成度矩阵图 章节名称 课程学习目标1 课程学习目标2 课程学习目标3 第1.1-1.7节 H M M 第2.1-2.7节 H H H 第3.1-3.8节 H 夕 H 第4.1-4.3节 H M H 第5.1-5.4节 H M 第6.1-6.4节 H H H 第7.1-7.5节 H H H 第8.1-8.4节 H M L (三)《高等数学》课程教学方法与课程学习目标的对应关系矩阵图 课程教学方法 可支撑的课程学习目标 1.根据《高等数学》课程的特点,采用板书 学习目标1:了解高等数学课程的地位与性 授课的方式进行教学。注重高等数学基本概 质,系统掌握高等数学的基本概念、基本解法 念、基本方法和基本理论的详细讲解。 和基本理论
第 8.4 节:傅里叶级数 3.重点:常数项级数的审敛法,幂级数,函数展开成幂级数及其应用,傅里叶级数。 4.难点:常数项级数的审敛法,幂级数求和,函数展开成幂级数,函数展开成傅里叶级数。 5 . 参考习题: 习题 8-1:第 1、5-10 题 习题 8-2:第 1-13 题 习题 8-3:第 1-7 题 习题 8-4:第 1-6 题 章节测试题:全部 6 . 学时:16 学时 (二)《高等数学》课程学习目标与教学内容达成度矩阵图 章节名称 课程学习目标 1 课程学习目标 2 课程学习目标 3 第 1.1-1.7 节 H M M 第 2.1-2.7 节 H H H 第 3.1-3.8 节 H H H 第 4.1-4.3 节 H M H 第 5.1-5.4 节 H L M 第 6.1-6.4 节 H H H 第 7.1-7.5 节 H H H 第 8.1-8.4 节 H M L (三)《高等数学》课程教学方法与课程学习目标的对应关系矩阵图 课程教学方法 可支撑的课程学习目标 1. 根据《高等数学》课程的特点,采用板书 授课的方式进行教学。注重高等数学基本概 念、基本方法和基本理论的详细讲解。 学习目标 1:了解高等数学课程的地位与性 质,系统掌握高等数学的基本概念、基本解法 和基本理论。 8