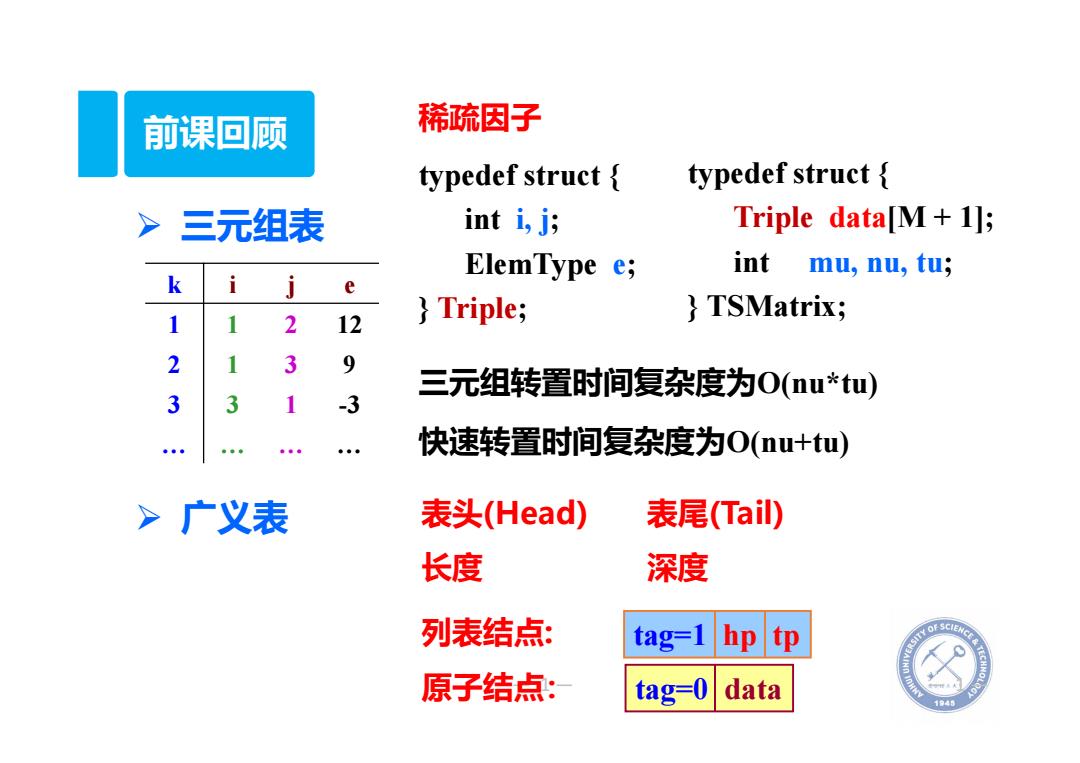
前课回顾 稀疏因子 typedef struct typedef struct > 三元组表 int i,j; Triple data[M+1]; ElemType e; int mu,nu,fu; k TSMatrix; 1 2 12 Triple; 2 3 9 三元组转置时间复杂度为O(nu*tu) 3 3 -3 快速转置时间复杂度为O(u+tu)) >广义表 表头(Head) 表尾(Tail) 长度 深度 列表结点: tag=1 hp tp 0 原子结点: tag-0 data 1945
— 1— — 1— 前课回顾 三元组表 广义表 稀疏因子 typedef struct { int i, j; ElemType e; } Triple; typedef struct { Triple data[M + 1]; int mu, nu, tu; } TSMatrix; 三元组转置时间复杂度为O(nu*tu) 快速转置时间复杂度为O(nu+tu) k ije 1 1 2 12 2 1 3 9 3 3 1 -3 … … … … 表头(Head) 表尾(Tail) 长度 深度 列表结点: 原子结点: tag=1 hp tp tag=0 data

学习要求 第六章树和二叉树 ■ 理解树的定义和基本术语,重点了解二叉树的 定义、性质、存储结构; ■掌握二叉树遍历的递归算法及它的典型运算: ■理解线索化二叉树的特性; 理解树、森林和二叉树间的相互转换规则; 掌握哈夫曼树的实现方法,理解构造哈夫曼编 码及带权路径长度的计算。 1945
— 2— — 2— 学习要求 理解树的定义和基本术语,重点了解二叉树的 定义、性质、存储结构; 掌握二叉树遍历的递归算法及它的典型运算; 理解线索化二叉树的特性; 理解树、森林和二叉树间的相互转换规则; 掌握哈夫曼树的实现方法,理解构造哈夫曼编 码及带权路径长度的计算。 第六章 树和二叉树
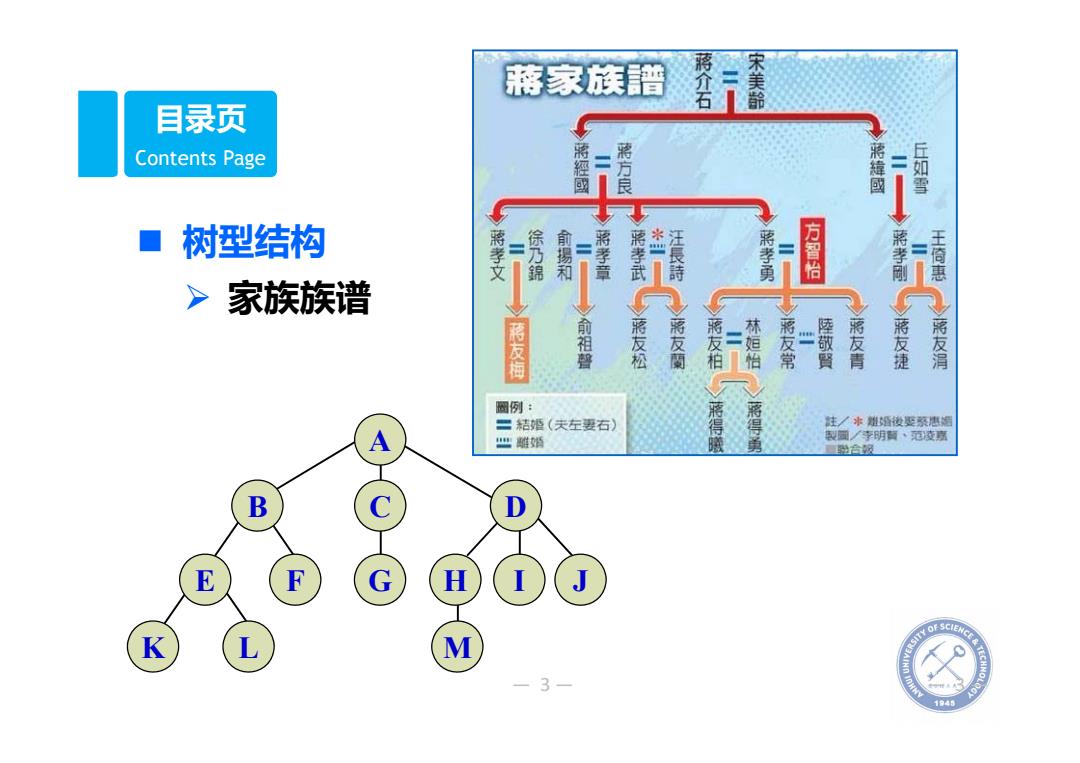
蔣家族普 蔣介石 宋美 目录页 Contents Page 蔣經國 蔣方良 蔣緯國 =1 丘如雪 树型结构 蔣孝文 徐乃锦 前場和 = 蔣孝章 蔣孝武 汪長詩 蔣孝勇 方智怡 蔣孝刚 =7 王倚惠 >家族族谱 友梅 俞祖 需友松 將友蘭 漓友柏 林运怡 需友常 陸敬賢 蔣友青 蔣友捷 蔣友涓 圆例: 二桔婚(夫左要右) A 四醮婚 蒋得哦 蔣得勇 柱本塑婚使雯系唐烟 製面/李明面、范麦京 台极 B C D E F G H K L M 3 1945
— 3— — 3— Contents Page 目录页 树型结构 家族族谱 I J A B C D E F G H K L M
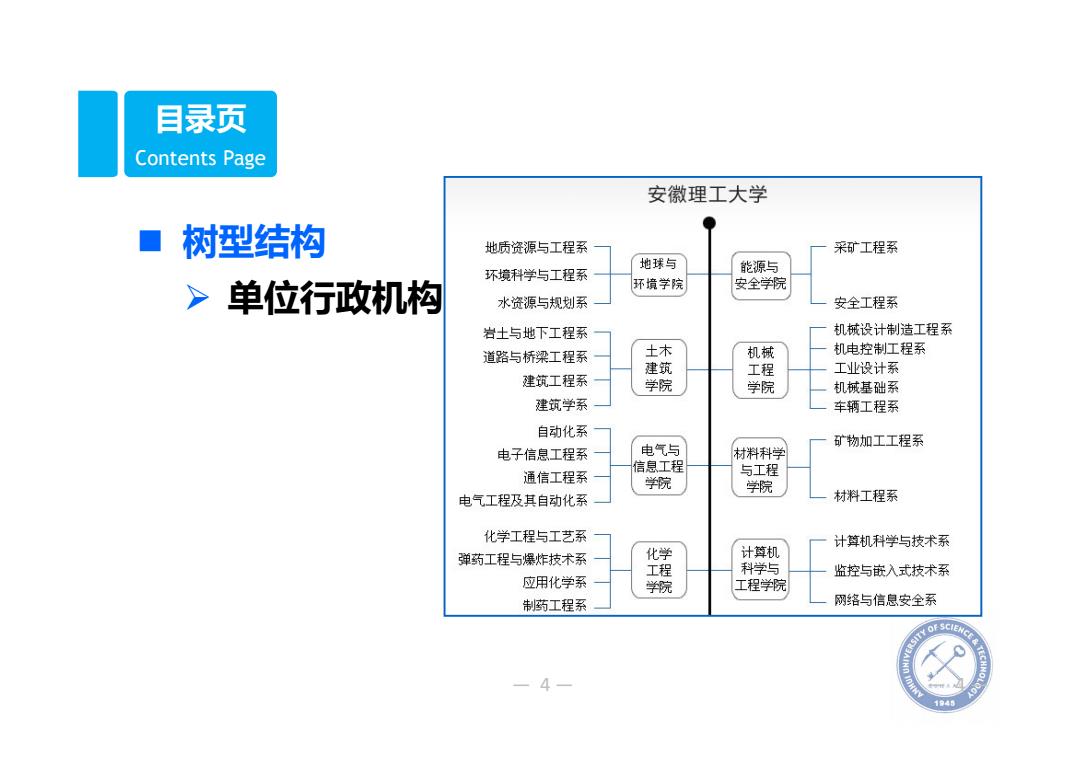
目录页 Contents Page 安徽理工大学 树型结构 地质资源与工程系 采矿工程系 地球与 环境科学与工程系 能源与 >单位行政机构 环境学院 安全学院 水资源与规划系 安全工程系 岩土与地下工程系 机械设计制造工程系 道路与桥梁工程系 土木 机械 机电控制工程系 建筑 工程 工业设计系 建筑工程系 学院 学院 机械基础系 建筑学系 车辆工程系 自动化系 电子信息工程系 电气与 矿物加工工程系 材料科学 信息工程 通信工程系 与工程 学院 学院 电气工程及其自动化系 材料工程系 化学工程与工艺系 计算机科学与技术系 弹药工程与爆炸技术系 化学 计算机 工程 科学与 监控与嵌入式技术系 应用化学系 学院 工程学院 制药工程系 网络与信息安全系 -4 1945
— 4— — 4— Contents Page 目录页 树型结构 单位行政机构的组织关系
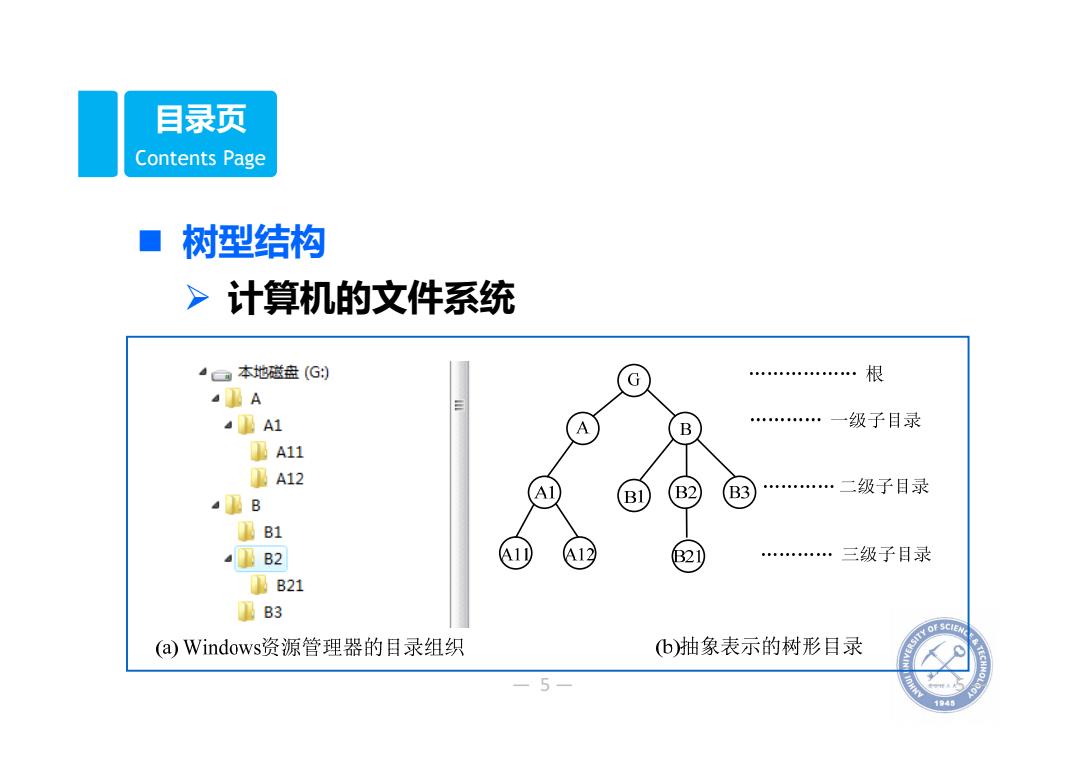
目录页 Contents Page 树型结构 >计算机的文件系统 4本地磁盘(G) G 00g 根 A A1 A B 级子目录 A11 A12 B2 B3 an 二级子目录 B B1 B2 A B2 三级子目录 B21 重B3 (a)Windows资源管理器的目录组织 b)抽象表示的树形目录 5
— 5— — 5— Contents Page 目录页 树型结构 计算机的文件系统
目录页 Contents Page 树的定义和基本术语 第六章 二叉树 树和二叉树 遍历二叉树和线索二叉树 树和森林 哈夫曼树及其应用 -6 1945
— 6— — 6— Contents Page 目录页 二叉树 遍历二叉树和线索二叉树 树的定义和基本术语 树和森林 哈夫曼树及其应用

6.1树的定义和基本术语 定义:树(Tree)是由n(n≥0)个数据元素的集合,当 集合为空时称为空树,否则它满足如下两个条件: (1)有且仅有一个特定的称为根(Root)的结点; (2)其余的结点可分为m(m>=0)个互不相交的 子集T,T2Tm,其中每个子集又是一棵树,并称 为根的子树(Subtree)。 除根外每个结点有且仅有一个直接前驱,但可以 有0个或多个直接后继。 7 1945
— 7— 6.1 树的定义和基本术语 定义:树(Tree)是由n(n≥0)个数据元素的集合,当 集合为空时称为空树,否则它满足如下两个条件: (1) 有且仅有一个特定的称为根(Root)的结点; (2) 其余的结点可分为m(m>=0)个互不相交的 子集T1,T2…Tm,其中每个子集又是一棵树,并称 为根的子树(Subtree)。 除根外每个结点有且仅有一个直接前驱,但可以 有0个或多个直接后继
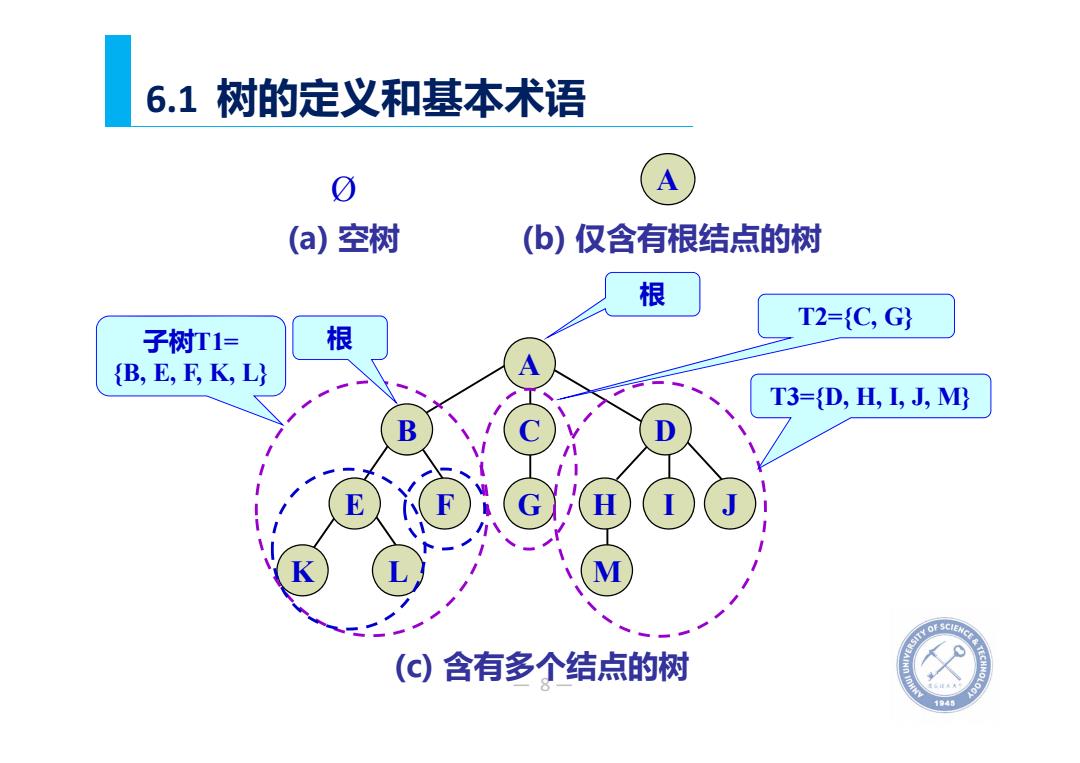
6.1树的定义和基本术语 A (a)空树 (b)仅含有根结点的树 根 T2={C,G} 子树加1= 根 (B,E,F,K,L) T3={D,H,I,J,0 (c)含有多个结点的树 1945
— 8— 6.1 树的定义和基本术语 Ø A (a) 空树 I J A B C D E F G H K L M (c) 含有多个结点的树 根 子树T1= {B, E, F, K, L} T2={C, G} T3={D, H, I, J, M} 根 (b) 仅含有根结点的树
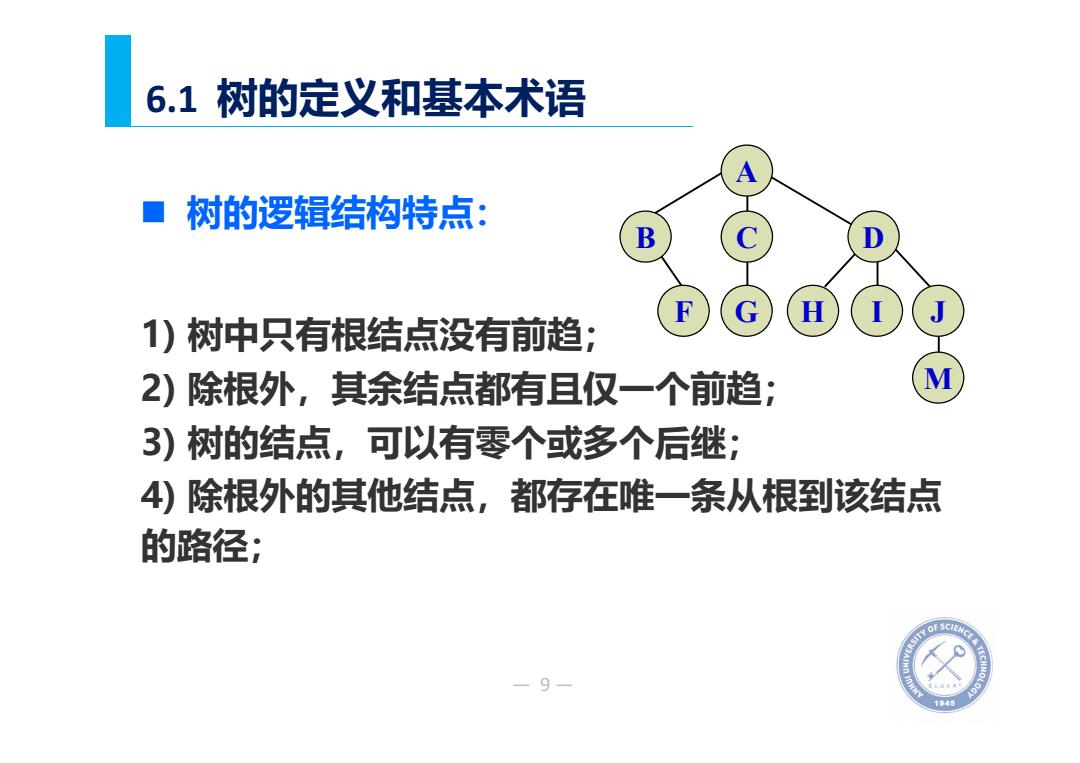
6.1树的定义和基本术语 A ■树的逻辑结构特点: B C D F G H 1)树中只有根结点没有前趋: 2)除根外,其余结点都有且仅一个前趋: M 3)树的结点,可以有零个或多个后继; 4)除根外的其他结点,都存在唯一条从根到该结点 的路径; -9- 145
— 9— 6.1 树的定义和基本术语 1) 树中只有根结点没有前趋; 2) 除根外,其余结点都有且仅一个前趋; 3) 树的结点,可以有零个或多个后继; 4) 除根外的其他结点,都存在唯一条从根到该结点 的路径; 树的逻辑结构特点: I J A B C D F G H M

6.1树的定义和基本术语 ■树的表示 A B D 1.二元组表示法 E F G H K M K=A,B,C,D,E,F,G,H,LJ,K,L,MY R={r} ={,,,,, ,,,,,} -10 1945
— 10 — 6.1 树的定义和基本术语 K={A,B,C,D,E,F,G,H,I,J,K,L,M} R={r} r={, , , , , , , , , , , } 1. 二元组表示法 树的表示 I J A B C D E F G H K L M