
第三章栈和队列 ·学习要点 一理解栈和队列的基本概念和各种存 储结构 一掌握栈和队列的各种基本操作 一了解栈在递归运算中的应用
第三章 栈和队列 • 学习要点 –理解栈和队列的基本概念和各种存 储结构; –掌握栈和队列的各种基本操作 –了解栈在递归运算中的应用

通常称,栈和队列是限定插入和删除 只能在表的“端点”进行的线性表。 线性表 栈 队列 Insert(L,i,x) Insert(S,n+1,x) Insert(Q,n+1,x) l≤isn+1 Delete(L,i,x)Delete(S,n,x) Delete(Q,1,x) l≤isn 栈和队列是两种常用的数据类型
通常称,栈和队列是限定插入和删除 只能在表的“端点”进行的线性表。 线性表 栈 队列 Insert(L, i, x) Insert(S, n+1, x) Insert(Q, n+1, x) 1≤i≤n+1 Delete(L, i, x) Delete(S, n, x) Delete(Q, 1, x) 1≤i≤n 栈和队列是两种常用的数据类型

3.1栈 3.2栈的应用举例 3.3递归 3.4 队列
3.1 栈 3.2 栈的应用举例 3.3 递归 3.4 队列

3.1栈
3.1 栈
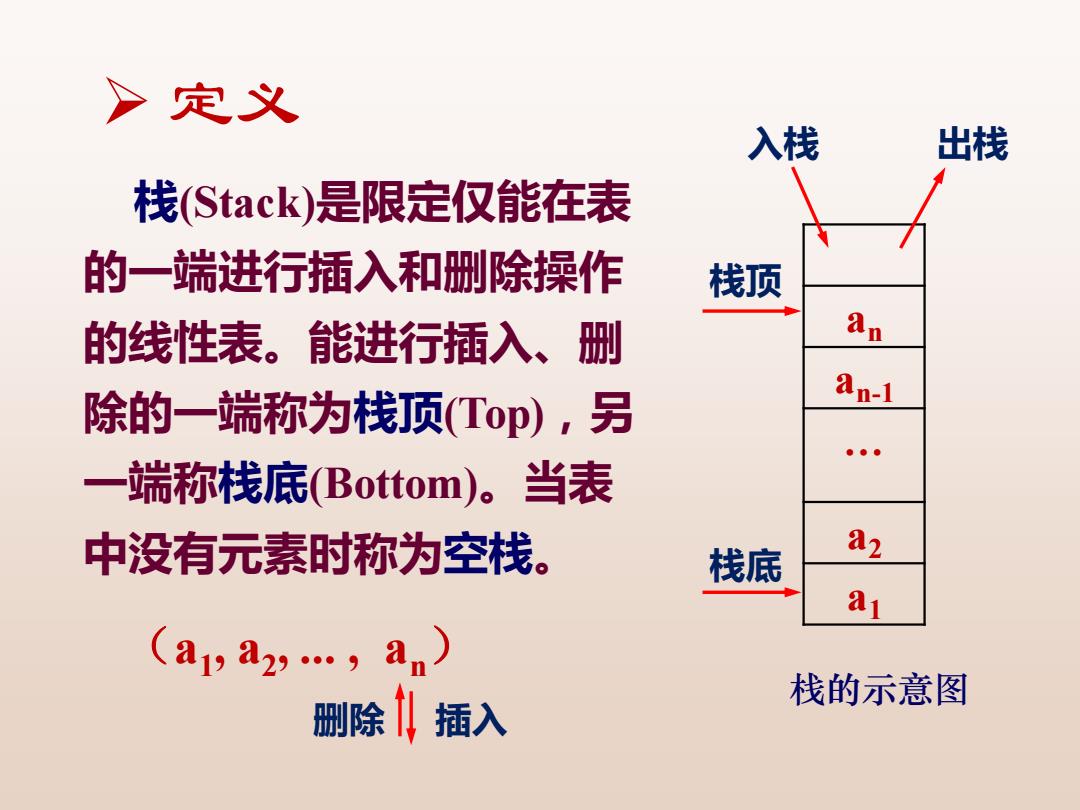
>定义 入栈 出栈 栈(Stack)是限定仅能在表 的一端进行插入和删除操作 栈顶 的线性表。能进行插入、删 An 除的一端称为栈顶(Top),另 an-1 。。 一端称栈底(Bottom)。当表 中没有元素时称为空栈。 栈底 a2 (a1pa2y…,an) 删除!插入 栈的示意图
an an-1 … a2 a1 入栈 出栈 栈顶 栈底 栈的示意图 栈(Stack)是限定仅能在表 的一端进行插入和删除操作 的线性表。能进行插入、删 除的一端称为栈顶(Top),另 一端称栈底(Bottom)。当表 中没有元素时称为空栈。 ➢ 定义 (a1 , a2 , ... , an) 删除 插入
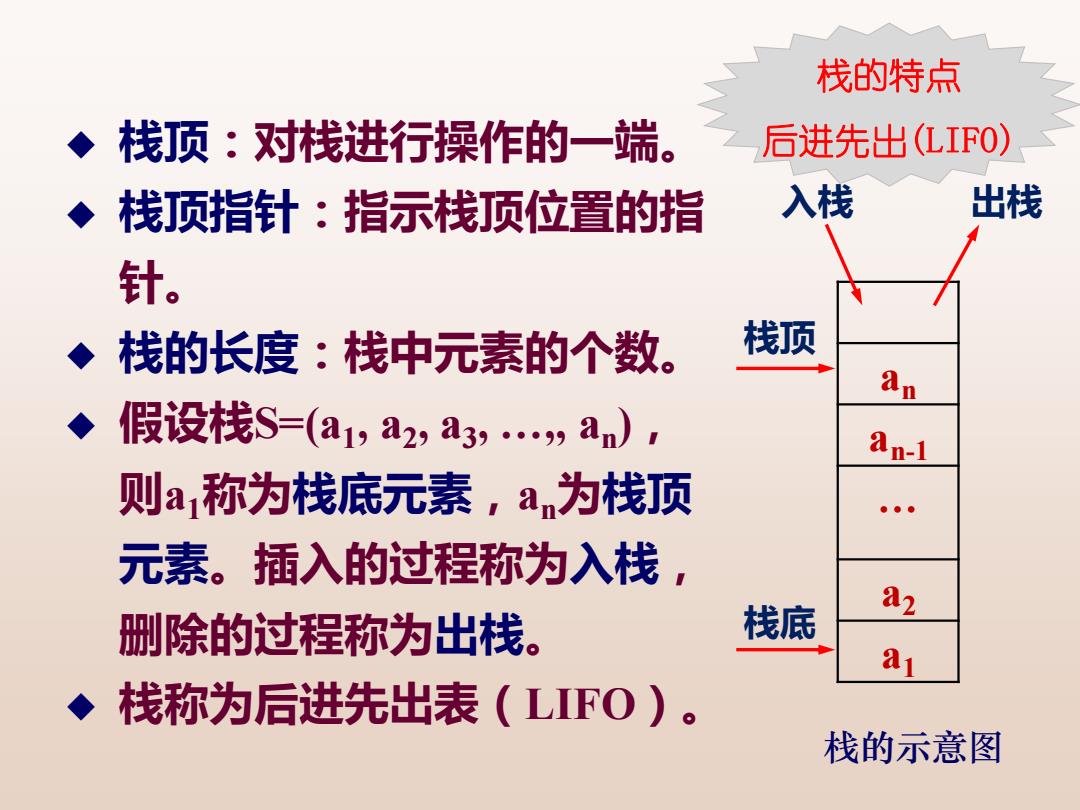
栈的特点 栈顶:对栈进行操作的一端。 后进先出(LIFO) 栈顶指针:指示栈顶位置的指 入栈 出栈 针。 栈的长度:栈中元素的个数。 栈顶 An 假设栈S-(a1,a2,a3,,an), an-1 则a1称为栈底元素,a为栈顶 元素。插入的过程称为入栈, a2 删除的过程称为出栈。 栈底 a1 ◆栈称为后进先出表(LIFO)。 栈的示意图
◆ 栈顶:对栈进行操作的一端。 ◆ 栈顶指针:指示栈顶位置的指 针。 ◆ 栈的长度:栈中元素的个数。 ◆ 假设栈S=(a1 , a2 , a3 , …,, an ), 则a1称为栈底元素,an为栈顶 元素。插入的过程称为入栈, 删除的过程称为出栈。 ◆ 栈称为后进先出表(LIFO)。 an an-1 … a2 a1 入栈 出栈 栈顶 栈底 栈的示意图 栈的特点 后进先出(LIFO)
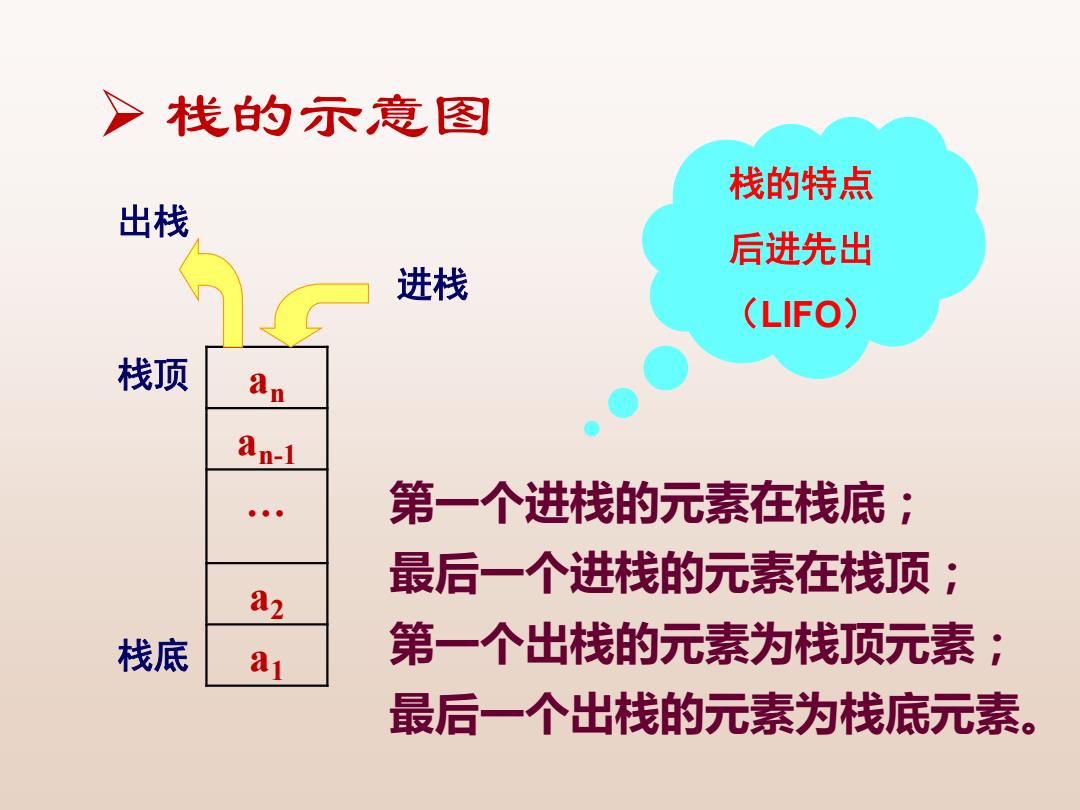
>栈的示意图 栈的特点 出栈 后进先出 进栈 (LIFO) 栈顶 an-1 第一个进栈的元素在栈底: 最后一个进栈的元素在栈顶: a2 栈底 aj 第一个出栈的元素为栈顶元素; 最后一个出栈的元素为栈底元素
➢ 栈的示意图 an an-1 … a2 a1 栈顶 栈底 出栈 进栈 第一个进栈的元素在栈底; 最后一个进栈的元素在栈顶; 第一个出栈的元素为栈顶元素; 最后一个出栈的元素为栈底元素。 栈的特点 后进先出 (LIFO)

抽象数据类型栈的定义: ADT Stack 数据对象: D=a ai EElemSet,i=1,2,...,n,n20 数据关系: R1={la-1,a∈D,i=2,,n} 约定a端为栈顶,a1端为栈底。 基本操作: ADT Stack
ADT Stack { 数据对象: D={ ai | ai ∈ElemSet, i=1,2,...,n, n≥0 } 数据关系: R1={ | ai-1 , ai∈D, i=2,...,n } 约定an 端为栈顶,a1 端为栈底。 基本操作: } ADT Stack 抽象数据类型栈的定义:

栈的基本操作: InitStack(&S) DestroyStack() StackEmpty(s) GetTop(S,&e) ClearStack(&S) Push(&S,e) Pop(&S,&e)
InitStack(&S) ClearStack(&S) StackEmpty(s) GetTop(S, &e) Push(&S, e) Pop(&S, &e) 栈的基本操作: DestroyStack(&S)

InitStack(&S) 操作结果:构造一个空栈S。 DestroyStack(&S) 初始条件:栈S已存在。 操作结果:栈S被销毁
InitStack(&S) 操作结果:构造一个空栈 S。 DestroyStack(&S) 初始条件:栈 S 已存在。 操作结果:栈 S 被销毁