
第六章 树和二叉树 ■理解树的定义和基本术语,重点了解二叉树的 定义、性质、存储结构: ■掌握二叉树遍历的递归算法及它的典型运算: ■理解线索化二叉树的特性以及寻找某结点的前 驱和后继的方法; ■理解树、森林和二叉树间的相互转换规则; ■掌握哈夫曼树的实现方法,理解构造哈夫曼编 码及带权路径长度的计算
第六章 树和二叉树 ◼理解树的定义和基本术语,重点了解二叉树的 定义、性质、存储结构; ◼掌握二叉树遍历的递归算法及它的典型运算; ◼理解线索化二叉树的特性以及寻找某结点的前 驱和后继的方法; ◼理解树、森林和二叉树间的相互转换规则; ◼掌握哈夫曼树的实现方法,理解构造哈夫曼编 码及带权路径长度的计算
树可表示具有分枝结构关系的对象 例1家族族谱 设某家庭有13个成员A、B、C、D、E F、G、H、I、J、K、L、M,他们之间的关 系可下图所示的树表示 B E 例2单位行政机构的组织关系
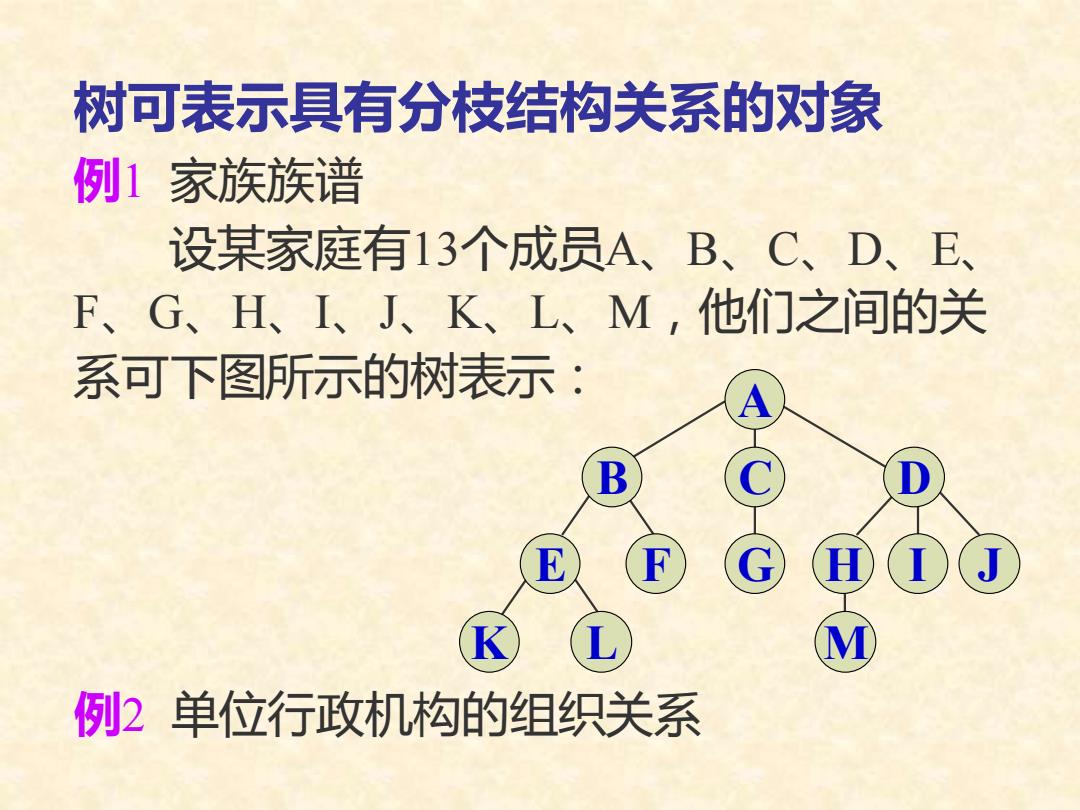
树可表示具有分枝结构关系的对象 例1 家族族谱 设某家庭有13个成员A、B、C、D、E、 F、G、H、I、J、K、L、M,他们之间的关 系可下图所示的树表示: 例2 单位行政机构的组织关系 I J A B C D E F G H K L M

树是常用的数据组织形式 有些应用中数据元素之间并不存在间分支 结构关系,但是为了便于管理和使用数据,将 它们用树的形式来组织。 例3计算机的文件系统 不论是Linux文件系统还是Windows文件系 统,所有的文件是用树的形式来组织的。 文件夹1 文件夹n 文件1 文件2 文件夹11文件夹12文件11文件12
树是常用的数据组织形式 有些应用中数据元素之间并不存在间分支 结构关系,但是为了便于管理和使用数据,将 它们用树的形式来组织。 例3 计算机的文件系统 不论是Linux文件系统还是Windows文件系 统,所有的文件是用树的形式来组织的。 文件夹1 文件夹n 文件1 文件2 文件夹11 文件夹12 文件11 文件12 /

6.1树的定义和基本术语 定义:树(Tree)是由n(n≥0)个数据元素的集合 当集合为空时称为空树,否则它满足如下两个 条件: (1)有且仅有一个特定的称为根(R0o)的结点, (2)其余的结点可分为m(m>=0)个互不相交的 子集T,T2.Tm,其中每个子集又是一棵树,并 称为根的子树Subtree)。 每棵子树的根结点有且仅有一个直接前驱 但可以有0个或多个直接后继
6.1 树的定义和基本术语 定义:树(Tree)是由n(n≥0)个数据元素的集合, 当集合为空时称为空树,否则它满足如下两个 条件: (1) 有且仅有一个特定的称为根(Root)的结点; (2) 其余的结点可分为m(m>=0)个互不相交的 子集T1 ,T2…Tm,其中每个子集又是一棵树,并 称为根的子树(Subtree)。 每棵子树的根结点有且仅有一个直接前驱, 但可以有0个或多个直接后继
0 A (a)空树 (b)仅含有根结点的树 B (c)含有多个结点的树
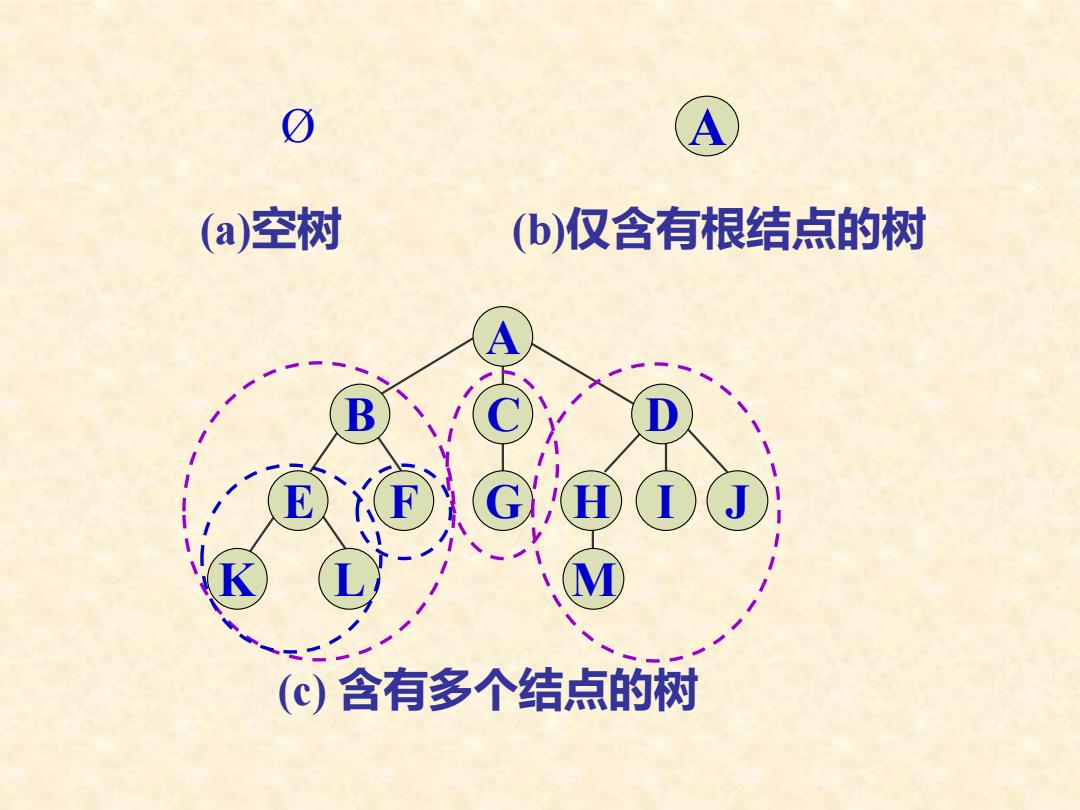
Ø A (a)空树 (b)仅含有根结点的树 I J A B C D E F G H K L M (c) 含有多个结点的树
树的逻辑结构特点: B 1)树中只有根结点没有前趋 2)除根外,其余结点都有且仅一个前趋 M 3)树的结点,可以有零个或多个后继; 4)除根外的其他结点,都存在唯一条从根到 该结点的路径; 5)树是一种分枝结构(除了一个称为根的结 点外)每个元素都有且仅有一个直接前趋 有且仅有零个或多个直接后继
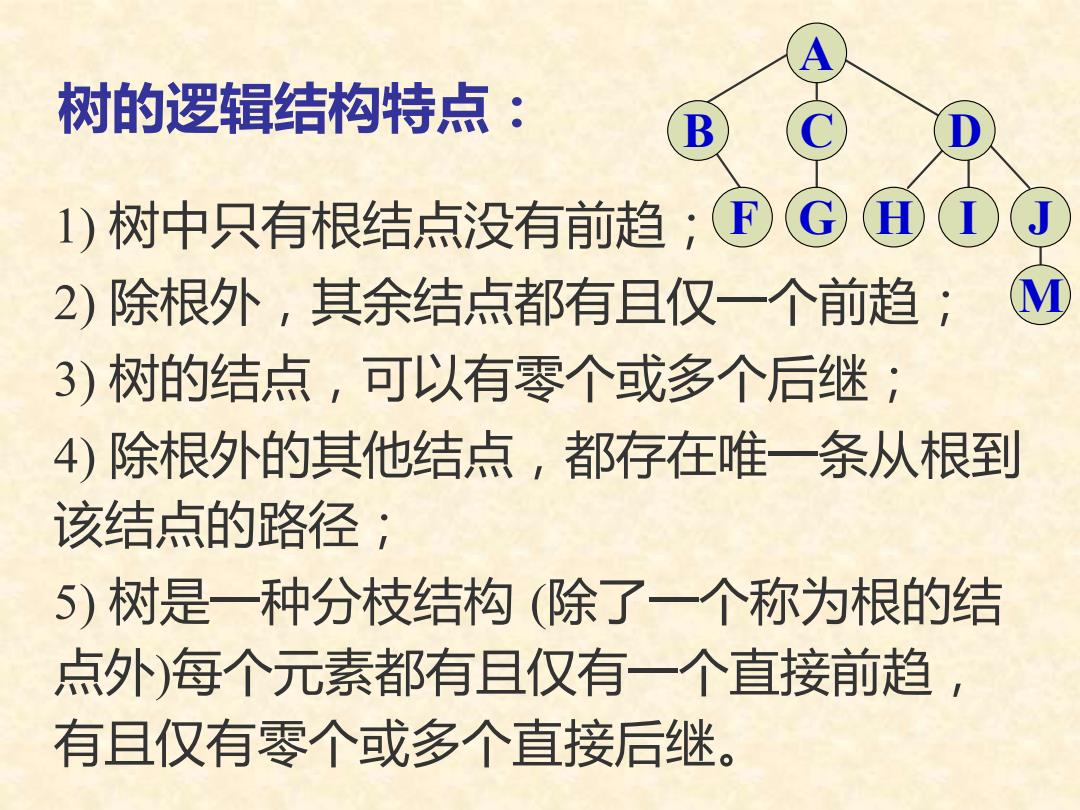
1) 树中只有根结点没有前趋; 2) 除根外,其余结点都有且仅一个前趋; 3) 树的结点,可以有零个或多个后继; 4) 除根外的其他结点,都存在唯一条从根到 该结点的路径; 5) 树是一种分枝结构 (除了一个称为根的结 点外)每个元素都有且仅有一个直接前趋, 有且仅有零个或多个直接后继。 树的逻辑结构特点: I J A B C D F G H M
树的表示 1.二元组表示法 A B D E F G H K K=A,B,C,D,E,F,G,H,I,J,K,L,MY R=T) I={(A,B),(A,C),(A,D),(B,E),(B,F),(C,G),(D,D, (D,D,D,J),(E,K),(E,L),H,M0}
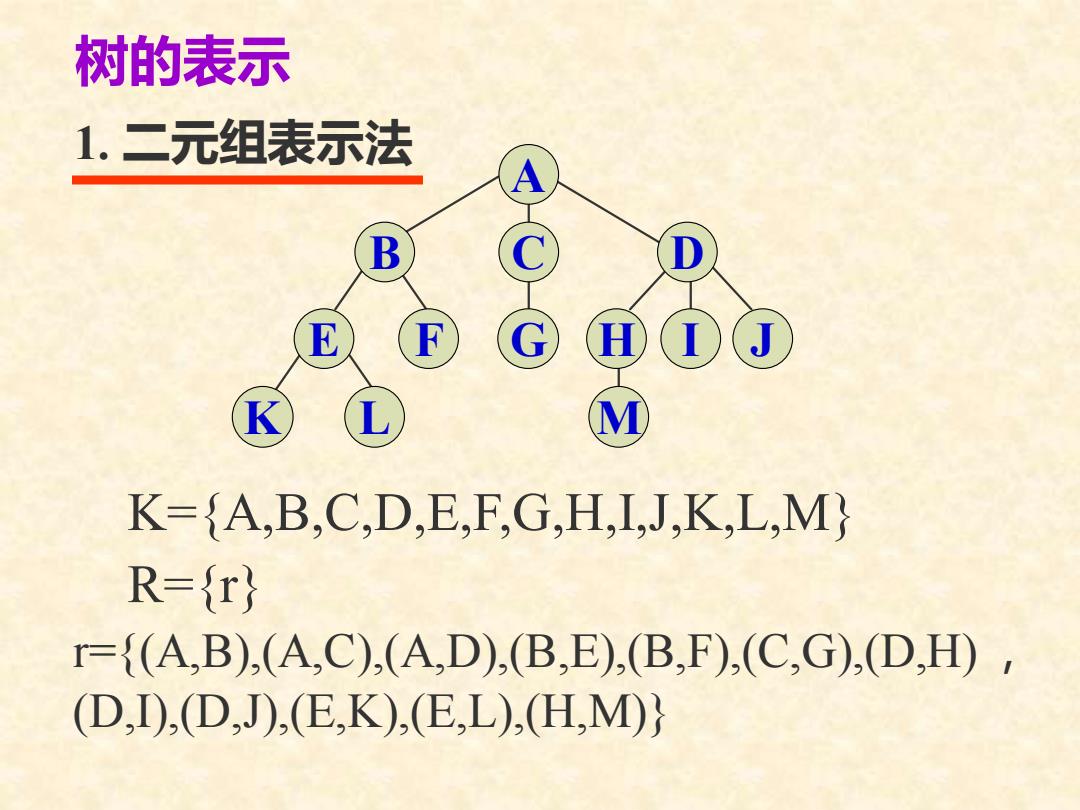
K={A,B,C,D,E,F,G,H,I,J,K,L,M} R={r} r={(A,B),(A,C),(A,D),(B,E),(B,F),(C,G),(D,H), (D,I),(D,J),(E,K),(E,L),(H,M)} 1. 二元组表示法 树的表示 I J A B C D E F G H K L M

2.凹入法表示法 A B E J K L F C G D H一 M I 树的凹入法表示
2. 凹入法表示法 A B E J K L F C G D H M I 树的凹入法表示

3.嵌套集合表示法 A B G K M 树的集合表示
3. 嵌套集合表示法 A B E J K L F C G D H M I 树的集合表示
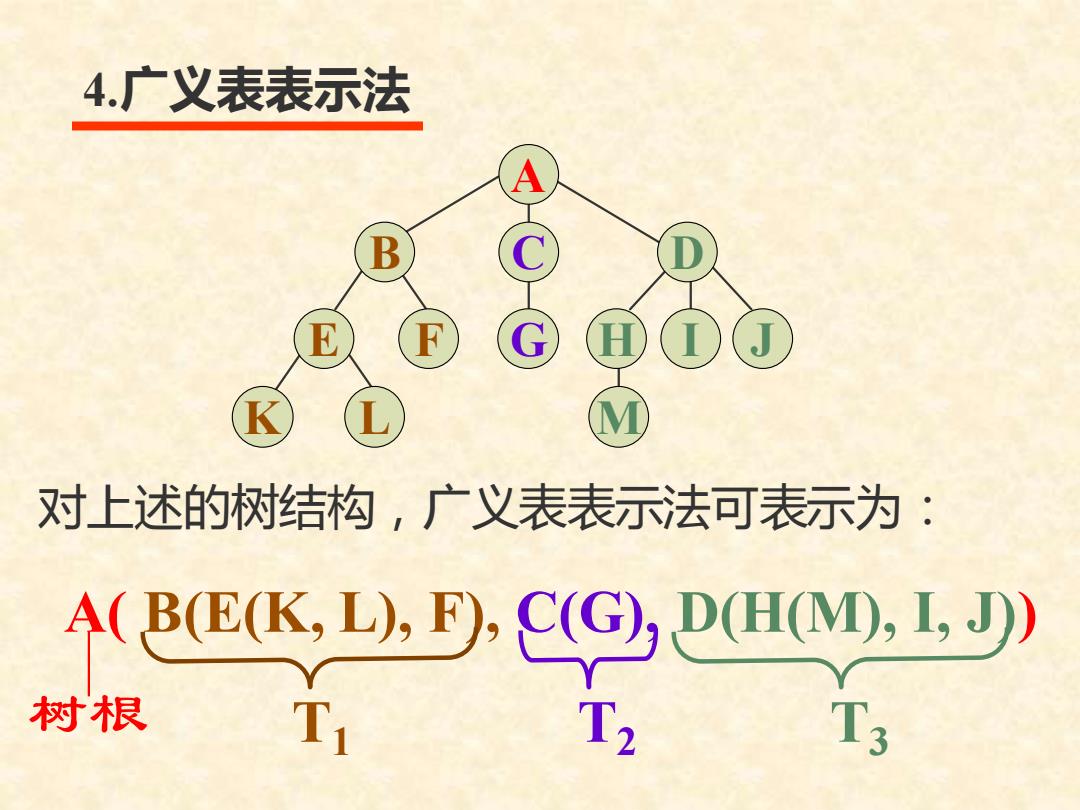
4.广义表表示法 A B E F G K 对上述的树结构,广义表表示法可表示为: A(B(E(K.L),F).C(G)D(H(MD),1,J)) 树根 Tu T T3
对上述的树结构,广义表表示法可表示为: 4.广义表表示法 A( B(E(K, L), F), C(G), D(H(M), I, J)) 树根 T1 T2 T3 I J A B C D E F G H K L M