
第四节 第六章 多无函数微分学的应用 一、空间曲线的切线与法平面 二、曲面的切平面与法线 三、多元函数的极值
第四节 一、空间曲线的切线与法平面 二、曲面的切平面与法线 多元函数微分学的应用 第六章 三、多元函数的极值

三、多元函数的极值 1.二元函数的极值 2.最值及其应用 3.条件极值
三、多元函数的极值 1.二元函数的极值 2.最值及其应用 3.条件极值

1.二元函数的极值 二元函数极值的定义
二元函数极值的定义 1. 二元函数的极值

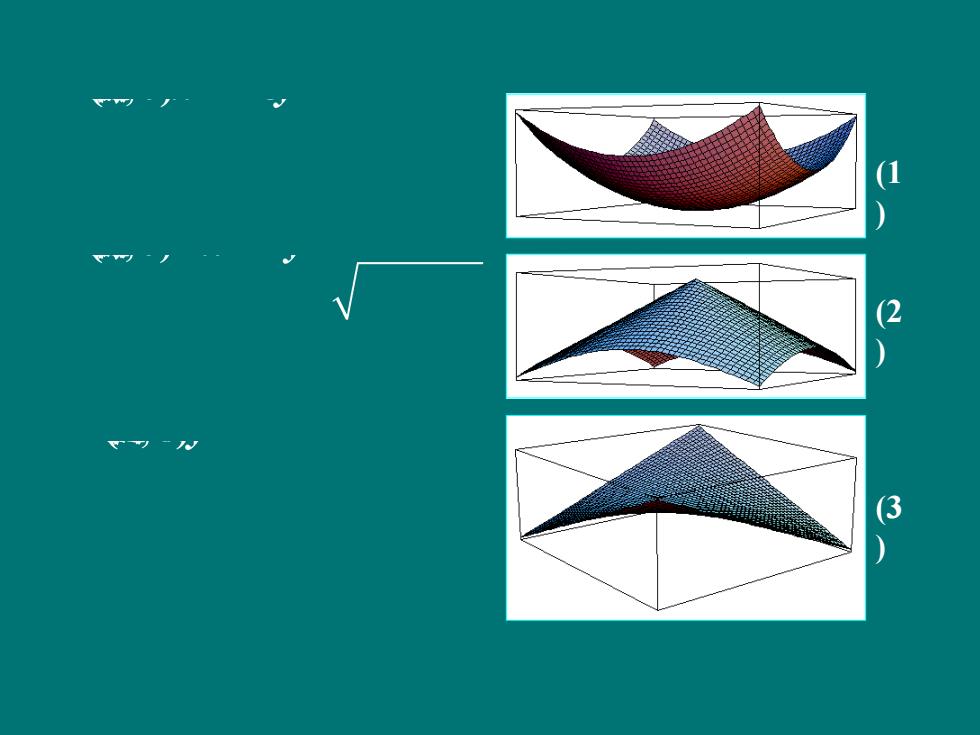
-了力yJ八-”xJ7人N) 极大值、极小值统称为极值. 使函数取得极值的点称为极值点
极大值、极小值统称为极值. 使函数取得极值的点称为极值点
(1) (2) (3)

二元函数取得极值的条件 使一阶偏导数同时为零的点,均称为函数的驻点 注意可导的极值点必为驻点,但驻点不一定是极值点 例如:点0,0)是函数zxy的驻点,但不是极值点: 问题:如何判定一个驻点是否为极值点?
二元函数取得极值的条件 使一阶偏导数同时为零的点,均称为函数的驻点. 注意 可导的极值点必为驻点,但驻点不一定是极值点. 问题:如何判定一个驻点是否为极值点? 例如:点(0,0)是函数z=xy的驻点,但不是极值点


求函数z口f(x,y)极值的一般步骤: 第一步 解方程组f(x,y)口0,f,(x,y)☐0 求出实数解,得驻点! 第二步 对于每一个驻点(x,y,), 求出二阶偏导数的值A、B、C. 第三步 定出AC口B的符号,再判定是否是极值 注:偏导数不存在点也有可能是极值点
注:偏导数不存在点也有可能是极值点

例1求函数f(x,y)=x3-y+3x2+3y2-9的极值 解:、先解方程组。·· 得驻点:(1,0),(1,2),(3,0),(-3,2) 求二阶偏导数
得驻点: (1, 0) , (1, 2) , (–3, 0) , (–3, 2). 解:先解方程组 求二阶偏导数 例1
