
概率伦与款理统外 引言 迄今为止,人们已发现很多大数定律 (laws of large numbers),所谓大数定律, 简单地说,就是大量数目的随机变量所 呈现出的规律,这种规律一般用随机变 量序列的某种收敛性来刻划。本章仅介 绍几个最基本的大数定律
引言 迄今为止,人们已发现很多大数定律 (laws of large numbers),所谓大数定律, 简单地说,就是大量数目的随机变量所 呈现出的规律,这种规律一般用随机变 量序列的某种收敛性来刻划。本章仅介 绍几个最基本的大数定律

概车纶与款理统外 大量随机现象的平均结果实际上是与各个 个别随机现象的特征无关,并且几乎不再是随机 的了.所有这些事实都应该由概率论作出理论上 的结论. 概率论中用来阐明大量随机现象平均结果的 稳定性的一系列定理统称为大数定律大数定律 是一种表现必然性与偶然性之间的辩证联系的规 律.由于大数定律的作用,大量的随机因素的总和 作用必然导致某种不依赖于个别随机事件的结果
大量随机现象的平均结果实际上是与各个 个别随机现象的特征无关,并且几乎不再是随机 的了.所有这些事实都应该由概率论作出理论上 的结论. 概率论中用来阐明大量随机现象平均结果的 稳定性的一系列定理统称为大数定律.大数定律 是一种表现必然性与偶然性之间的辩证联系的规 律.由于大数定律的作用,大量的随机因素的总和 作用必然导致某种不依赖于个别随机事件的结果

概率伦与款程统外 §5.1大数定律 >讨论“概率是频率的稳定值”的确切含义; >给出几种大数定律: 切比雪夫大数定律 伯努利大数定律 辛钦大数定律
§5.1 大数定律 ➢ 讨论 “概率是频率的稳定值”的确切含义; ➢ 给出几种大数定律: 切比雪夫大数定律 伯努利大数定律 辛钦大数定律
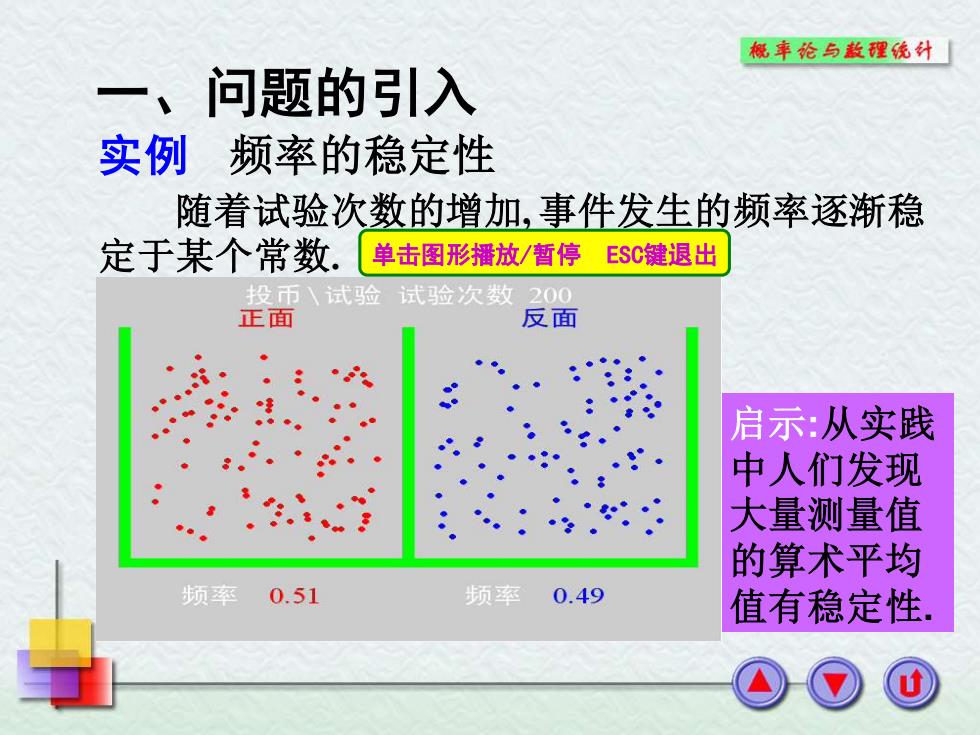
概车纶与款理统外「 一、问题的引入 实例 频率的稳定性 随着试验次数的增加,事件发生的频率逐渐稳 定于某个常数. 单击图形播放/暂停ESC键退出 投币试验试验次数 200 正面 反面 启示:从实践 中人们发现 大量测量值 的算术平均 频率 0.51 频率 0.49 值有稳定性
一、问题的引入 实例 频率的稳定性 随着试验次数的增加, 事件发生的频率逐渐稳 定于某个常数. 启示:从实践 中人们发现 大量测量值 的算术平均 值有稳定性. 单击图形播放/暂停 ESC键退出

概率伦与款理统外 二、基本定理 定理一(切比雪夫大数定律) 切比雪夫 设随机变量X1,X2,.,Xn,.相互独立, 且具有相同的数学期和方差:E(Xk)=4, D(Xk)=o2(k=1,2,),作前n个随机变量 的算术平均X=∑X, 则对于任意正 n k=l 数ε有 州-水=2x“<-1 1-→a0
二、基本定理 定理一(切比雪夫大数定律) 数 有 的算术平均 则对于任意正 作 前 个随机变量 且具有相同的数学期望和方差: 设随机变量 相互独立 , 1 ( ) ( 1, 2, ), ( ) , , , , , , 1 2 1 2 = = = = = n k k k k n X n X D X k n E X X X X 切比雪夫 1. 1 lim {| | } lim 1 = − = − = → → n k k n n X n P X P

概率伦与散理统针 表达式的意义 X-4K是一个随机事件等式表 明,当n→oo时这个事件的概率趋五, 即对于任意正数e,当n充分大时,不 等式|又-4K成立的概率很大 lim P{X-uk e)=lim P I->oo 2x-4=
1. 1 lim {| | } lim 1 = − = − = → → nk k n n X n P X P | | . , , , 1, {| | } , 等 式 成立的概率很大 即对于任意正数 当 充分大时 不 明 当 时这个事件的概率趋于 是一个随机事件 等式表 − → − X n n X 表达式的意义

概華论与款醒硫外 证明 2]2E0Xa=“ D(n 由切比雪夫不等式可得 x-1- 在上式中令n→∞,并注意到概率不能大于1,侧 P2,-心
证明 ( ) 1 1 1 1 = = = n k k n k k E X n X n E , 1 = n = n ( ) 1 1 1 2 1 = = = n k k n k k D X n X n D , 1 2 2 2 n n n = = 由切比雪夫不等式可得 1 , 1 2 2 1 n X n P n k k − − = 在上式中令n → , 并注意到概率不能大于1, 则 1. 1 1 = − = n k Xk n P

概车纶与款理统外 说明: 当n很大时,随机变量X1,X2,Xn的算术平 均∑X接近于数学期望 n k=1 E(X1)=E(X2)=.=E(Xk)=4, (这个接近是概率意义下的接近) 即在定理条件下,n个随机变量的算术平均,当n 无限增加时,几乎变成一个常数
说明: ( ) ( ) ( ) , 1 , , , , 1 2 1 1 2 = = = = = k n k k n E X E X E X X n n X X X 均 接近于数学期望 当 很大时 随机变量 的算术平 (这个接近是概率意义下的接近) 即在定理条件下, n个随机变量的算术平均, 当n 无限增加时, 几乎变成一个常数

概華论与款程统外 定理一的另一种叙述: 设随机变量X1,X 且具有相同的数学期 设,Y2,Yn是一个随 机变量序列a是一个常 D(Xk)=o2(k=1,2, 数,若对于任意正数8 依概率收敛于,肌又 有lim P(Y-ak}=1, 则称序列Y,Y,.,Y, 依概率收敛于,记为 Ynp→a
, . 1 ( ) ( 1, 2, ), ( ) , , , , , , 1 2 1 2 ⎯→ = = = = = P n k k k k n X X n D X k X E X X X X 依概率收敛于 即 则序列 且具有相同的数学期望和方差: 设随机变量 相互独立 Y a a Y Y Y P Y a a Y Y Y P n n n n n ⎯→ − = → 依概率收敛于 记 为 则称序列 有 数 若对于任意正数 机变量序列 是一个常 设 是一个随 , , , , lim {| | } 1, , , , , , 1 2 1 2 定理一的另一种叙述:

概车纶与款理统外 依概率收敛序列的性质: 设XnP→a,ynp→b, 又设函数g(K,y)在点(a,b)连续, 则g(Xn,Yn)P→g(a,b)
依概率收敛序列的性质: ( , ) ( , ) , , , 又设函数 在 点 连 续 设 g x y a b X a Y b P n P n ⎯→ ⎯→ g(X ,Y ) g(a, b). P 则 n n ⎯→