
第六章并行算法的基本设计技术 6.1划分设计技术 6.2分治设计技术 63平衡树设计技术 6.4倍增设计技术 6.5流水线设计技术
第六章 并行算法的基本设计技术 6.1 划分设计技术 6.2 分治设计技术 6.3 平衡树设计技术 6.4 倍增设计技术 6.5 流水线设计技术

6.1划分设计技术 6.1.1均匀划分技术 6.1,2方根划分技术 6.1.3对数划分技术 6.1,4功能划分技术
6.1 划分设计技术 6.1.1 均匀划分技术 6.1.2 方根划分技术 6.1.3 对数划分技术 6.1.4 功能划分技术

归并排序(Merge Sort) A merge sort works as follows: If the list is of length o or 1,then it is already sorted. Otherwise: Divide the unsorted list into two sublists of about half the size. 米 Sort each sublist recursively by re-applying the merge sort. Merge the two sublists back into one sorted list. 2011/10/25
A merge sort works as follows: If the list is of length 0 or 1, then it is already sorted. Otherwise: Divide the unsorted list into two sublists of about half the size. Sort each sublist recursively by re‐applying the merge sort. Merge the two sublists back into one sorted list. 归并排序(Merge Sort) 5 2011/10/25

归并排序(Merge Sort.) 米 Merge sort incorporates two main ideas to improve its runtime: A small list will take fewer steps to sort than a large list. Fewer steps are required to construct a sorted list from two sorted lists than from two unsorted lists.For example,you only have to traverse each list once if they're already sorted. 6 2011/10/25
Merge sort incorporates two main ideas to improve its runtime: A small list will take fewer steps to sort than a large list. Fewer steps are required to construct a sorted list from two sorted lists than from two unsorted lists. For example, you only have to traverse each list once if they're already sorted. 归并排序(Merge Sort) 6 2011/10/25

归并排序示例 2011/10/25
归并排序示例 7 2011/10/25

均匀划分技术 划分方法 n个元素A[1.n分成p组,每组A[i-1)n/p+1.in/p,i=1~p 米 示例:MIMD-SM模型上的PSRS排序 begin (I)均匀划分:将n个元素A[1n均匀划分成p段,每个p:处理 A[-1)n/p+1.in/p] (2)局部排序:p调用串行排序算法对A[-1)n/p+1.in/p排序 (3)选取样本:p:从其有序子序列A[-1)n/p+1.in/p]中选取p个样本元素 (4)样本排序:用一台处理器对个样本元素进行串行排序 (⑤)选择主元:用一台处理器从排好序的样本序列中选取p-1个主元,并 播送给其他p (⑥)主元划分:p按主元将有序段A[-1)n/p+1in/p划分成p段 (⑦全局交换:各处理器将其有序段按段号交换到对应的处理器中 (⑧)归并排序:各处理器对接收到的元素进行归并排序 end. 2011/10/25
划分方法 n个元素A[1..n]分成p组,每组A[(i-1)n/p+1..in/p],i=1~p 示例:MIMD-SM模型上的PSRS排序 begin (1)均匀划分:将n个元素A[1..n]均匀划分成p段,每个pi处理 A[(i-1)n/p+1..in/p] (2)局部排序:pi调用串行排序算法对A[(i-1)n/p+1..in/p]排序 (3)选取样本:pi从其有序子序列A[(i-1)n/p+1..in/p]中选取p个样本元素 (4)样本排序:用一台处理器对p 2个样本元素进行串行排序 (5)选择主元:用一台处理器从排好序的样本序列中选取p-1个主元,并 播送给其他pi (6)主元划分:pi按主元将有序段A[(i-1)n/p+1..in/p]划分成p段 (7)全局交换:各处理器将其有序段按段号交换到对应的处理器中 (8)归并排序:各处理器对接收到的元素进行归并排序 end. 8 2011/10/25 均匀划分技术
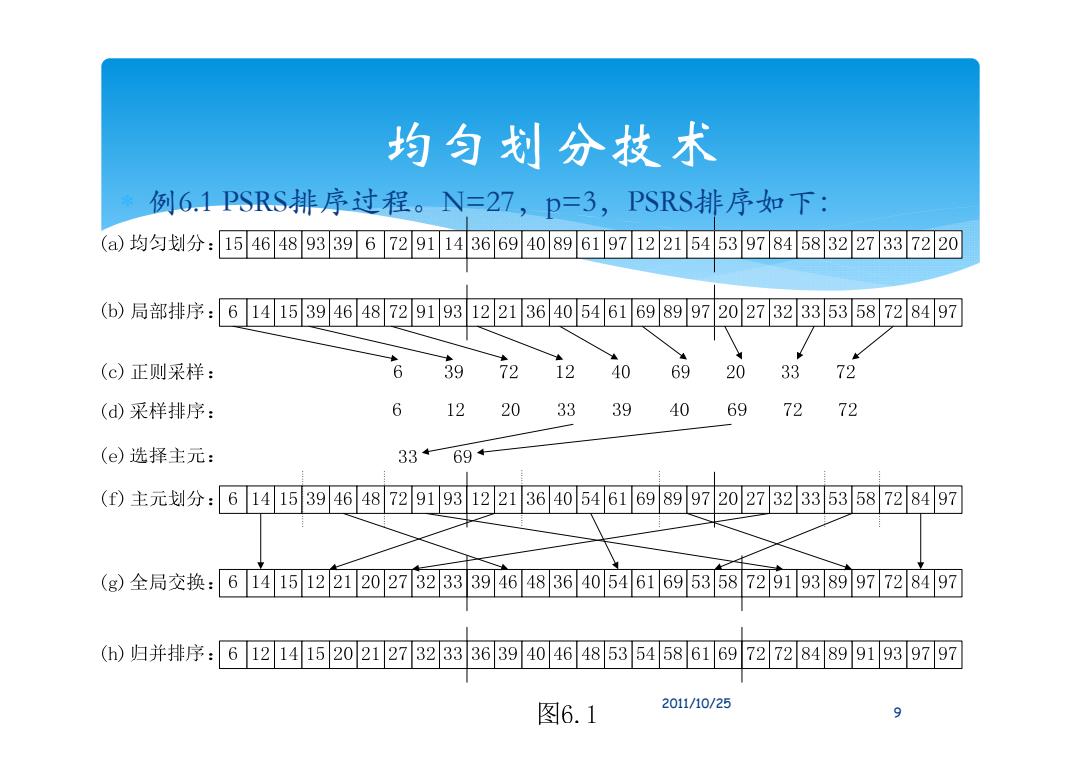
均匀划分技术 例6.1PSRS排序过程。N=27,p=3,PSRS排序如下: ()均匀划分:15464893396729114366940896197122154539784583227337220 (b)局部排序:61415394648729193122136405461698997202732335358728497 (c)正则采样: 639 72 12 40 69 20 33 72 (d)采样排序: 6 12 20 33 39 40 697272 (e)选择主元: 3369+ (f)主元划分:61415394648729193122136405461698997202732335358728497 (g)全局交换:61415122120273233394648364054616953587291938997728497 (h)归并排序:61214152021273233363940464853545861697272848991939797 图6.1 2011/10/25 9
均匀划分技术 例6.1 PSRS排序过程。N=27,p=3,PSRS排序如下: 9 2011/10/25

6.1划分设计技术 6.1.1均匀划分技术 6.1.2方根划分技术 6.1.3对数划分技术 6.1,4功能划分技术
6.1 划分设计技术 6.1.1 均匀划分技术 6.1.2 方根划分技术 6.1.3 对数划分技术 6.1.4 功能划分技术

方根划分技术 划分方法 n个元素A[1.n]分成A[i-1)n(1/2)+1in^(1/2,i=1~n^(1/2) 米 示例:SMD-CREW模型上的k=pa]Valiant)归并(1975年发表) /有序组A[1p小、B1ql,(假设p<=q),处理器数k=LVpg begin ()方根划分:A,B分别按Vp和Vg份成若干段(i=1~Vpj=1~」; 2)段间比较:A划分元与B划分元比较(至多DLg对), 确定A划分元应插入B中的区段; (③)段内比较:A划分元与B相应段内元素进行比较,并插入适当的位置; (4)递归归并:B按插入的A划分元重新分段,与A相应段(A除去原划分元) 构成了成对的段组,对每对段组递归执行(1)~(3),直至A 组为0时,递归结束;各组仍按k=VP9分配处理器; end. 2011/10/25 11
方根划分技术 划分方法 n个元素A[1..n]分成A[(i-1)n^(1/2)+1..in^(1/2)],i=1~n^(1/2) 示例:SIMD-CREW模型上的 Valiant归并(1975年发表) //有序组A[1..p]、B[1..q], (假设p<=q), 处理器数 begin (1)方根划分: A,B分别按 ; (2)段间比较: A划分元与B划分元比较(至多 对), 确定A划分元应插入B中的区段; (3)段内比较: A划分元与B相应段内元素进行比较,并插入适当的位置; (4)递归归并: B按插入的A划分元重新分段,与A相应段(A除去原划分元) 构成了成对的段组,对每对段组递归执行(1)~(3),直至A 组为0时,递归结束; 各组仍按 分配处理器; end. i p 和 j q 分成若干段(i 1 ~ p 、j 1 ~ q ) 11 2011/10/25 k pq k pq p q k pq

方根划分技术 ■示例:A=1,3,8,9,11,13,15,16,p=8;B={2,4,5,6,7,10,12,14,179=9 A: 138*911 13*1516 (p=8,VD3」2 (1)(2) B: 245* 10* 121417*(g=9,V53g」3) A: 138*911 13*1516 3){ B: 245*6 10*121417* A1:13 (P1=2)1A2:911(P2=2)1Az:1516 B1:245678(q1=6)B2:101213(q2=3)B3:1417 A1:13* (P1=2)1 B1:245*678*(q1=6 A11:1* A11 B11:23*B12:45678 0 234567 11 A: 2011/10/25
示例: A={1,3,8,9,11,13,15,16},p=8; B={2,4,5,6,7,10,12,14,17},q=9 A: 1 3 8* 9 11 13* 15 16 B: 2 4 5* 6 7 10* 12 14 17* (p 8, p 3, p 2) (q 9, q 3, q 3) (1)(2) A: 1 3 8* 9 11 13* 15 16 B: 2 4 5* 6 7 10* 12 14 17* (3) A1: 1 3 (p1=2) A2: 9 11 (p2=2) A2: 15 16 B1: 2 4 5 6 7 8(q1=6) B2: 10 12 13(q2=3) B3: 14 17 A1: 1 3* (p1=2) ...... ...... B1: 2 4 5* 6 7 8*(q1=6) ...... ...... A11: 1* A11: ...... ...... B11: 2 3* B12: 4 5 6 7 8 ...... ...... A: B: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 12 2011/10/25 方根划分技术