
第一章小结 1.热力学第一定律 热力学第一定律是能量守恒与转化定律在热现 象领域内所具有的特殊形式,说明热力学能、热和 功之间可以相互转化,但总的能量不变。 △U=U2-U1=2+W dU=8Q+δW
第一章 小 结 1. 热力学第一定律 热力学第一定律是能量守恒与转化定律在热现 象领域内所具有的特殊形式,说明热力学能、热和 功之间可以相互转化,但总的能量不变。 U Q W U U 2 1 = − = + dU Q W = +

2.定压热和定容热 (1) dU=δ2,(dV=0,δW=0) △U=Ow δQ。=dH(p=0,δW=0) △H=Op def H=U+PV
2. 定压热和定容热 (1) dU QV = = U QV , ) f (d 0 0 V W = = d Q H p = = H Qp f (d 0, 0) p W = = def H U pV = +

2.定压热和定容热 (2) c(T) def S0 (单纯pVT变化,W=0) dT c,-0().c-0】 wH=0,=∫C,dr (等压,非膨胀功为零) △U=Q,=∫C,dT(等容,非膨胀功为零)
2. 定压热和定容热 (2) ( ) def d = Q C T T (单纯pVT变化, Wf=0 ) ( ) d p p Q C T T = p H T = ( ) d V V Q C T T = V U T = H Q C T = = p pd (等压,非膨胀功为零) U Q C T = = V Vd (等容,非膨胀功为零)
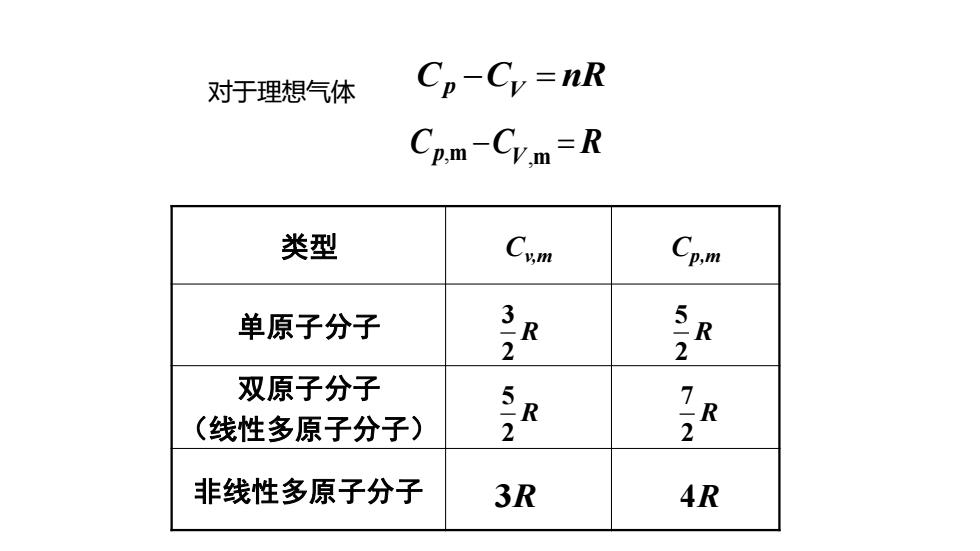
对于理想气体 Cp-Cy=nR Cp.m-Cy.m=R 类型 Cum Cp.m 单原子分子 E 2 R 双原子分子 (线性多原子分子) R 21 非线性多原子分子 3R 4R
对于理想气体 C C nR p V − = , p m V,m C C R − = 类型 Cv,m Cp,m 单原子分子 双原子分子 (线性多原子分子) 非线性多原子分子 3 2 R 5 2 R 7 2 R 5 2 R 3R 4R

3.理想气体可逆过程方程 (1)定温可逆过程 pV=K (2)绝热可逆过程 pV7=K TVY-1=K2 pl-YTY=K3 式中,K,K2,K3均为常数,y=Cp/Cy
3. 理想气体可逆过程方程 (1)定温可逆过程 (2)绝热可逆过程 pV = K 1 3 p T K − = 1 pV K = 1 2 TV K − = 式中,K K K 1 2 3 , , 均为常数, / C C p V =
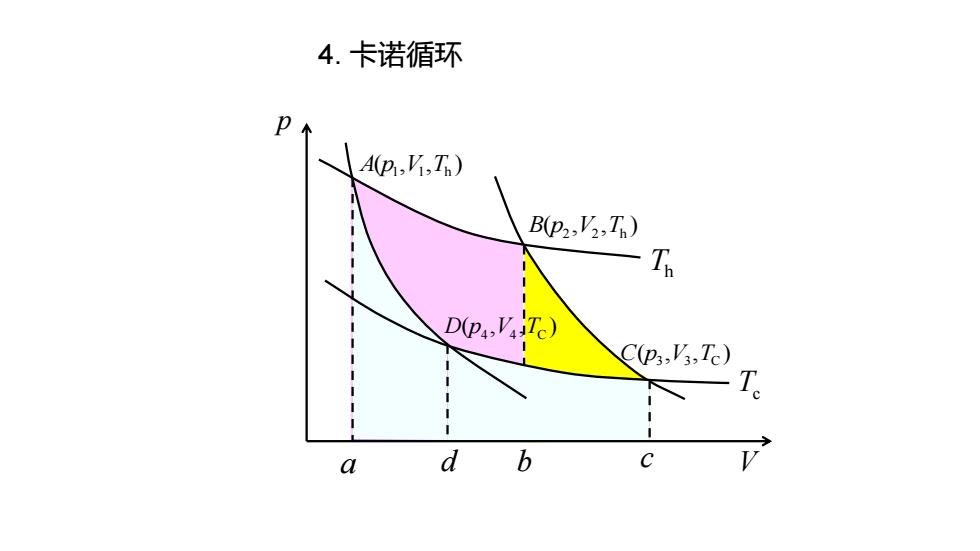
4.卡诺循环 p Ap,T)) B(p2,V2,Th) 6 D4,'4Te) C(ps.V3,Tc T a d b c P
4. 卡诺循环 p 1 1 h A p V T ( , , ) 2 2 h B p V T ( , , ) 3 3 C C p V T ( , , ) 4 4 C D p V T ( , , ) V Th Tc a d b c

热机的效率 -W 1= O 1=1- -W_2+.=1+ 7= T 2.2. g+9=0 T。'T 制冷效率 B= 2'-T W T-T
h W Q − = c h 1 T T = − h c c h h h 1 W Q Q Q Q Q Q − + = = = + 0 c h c h Q Q T T + = ' c c h c Q T W T T = = − 热机的效率 制冷效率

5.节流过程和焦汤系数 节流过程是一个恒焓过程 4-T>0 经节流膨胀后,气体温度降低。 J-T<0 经节流膨胀后,气体温度升高。 八-T=0 经节流膨胀后,气体温度不变
5. 节流过程和焦汤系数 节流过程是一个恒焓过程 J-T ( )H T p = J-T >0 经节流膨胀后,气体温度降低。 J-T <0 经节流膨胀后,气体温度升高。 J-T =0 经节流膨胀后,气体温度不变

6.过程W、Q、△U、△H的计算 (1)理想气体单纯即VT变化过程 变温过程 AU=∫C,dr=n:Cndn AH-C,T-nCdT -P(V-V)(等外压) C (恒容) △U (绝热) =∫C,dn=5-y Q=△U-W y-1
6.过程W、Q、ΔU、 ΔH的计算 (1)理想气体单纯pVT变化过程 变温过程 2 2 1 1 , T T V V m T T = = U C dT n C dT 2 2 1 1 , T T p p m T T = = H C dT n C dT W p dV = − = e 2 1 ( ) e − − p V V (等外压) 0 (恒容) U (绝热) 2 1 T V T = C dT 2 2 1 1 1 p V p V − = Q − = − U W
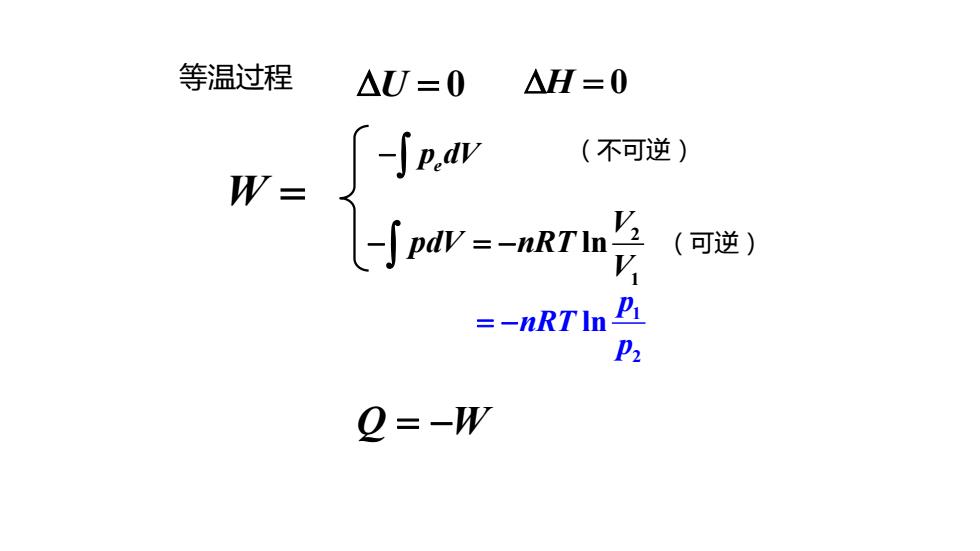
等温过程 △U=0 △H=0 W- -∫p.aw (不可逆) \-Spdv-wRTi (可逆) =-nRTIn P2 2=-W
等温过程 = U 0 = H 0 W = e − p dV (不可逆) 2 (可逆) 1 lnV pdV nRT V − = − 1 2 ln p nRT p = − Q W = −