
第六节空间曲线及其方程
第六节 空间曲线及其方程

空间曲线及其方程 空间曲线的一段方程 二、 空间曲线的参数方程 三、空间曲线在坐标面上的投影
空间曲线及其方程 一、空间曲线的一般方程 二、空间曲线的参数方程 三、空间曲线在坐标面上的投影

空间曲线及其方程 空间曲线的一殷方程 二、空间曲线的参数方程 三、空间曲线在坐标面上的投影
空间曲线及其方程 一、空间曲线的一般方程 二、空间曲线的参数方程 三、空间曲线在坐标面上的投影
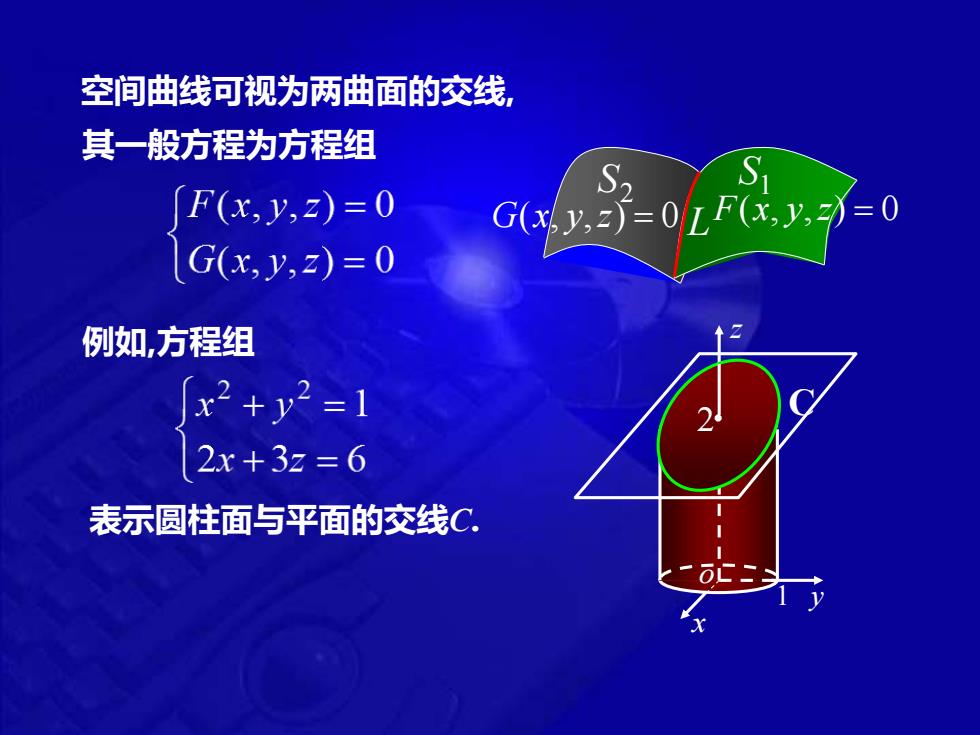
空间曲线可视为两曲面的交线, 其一般方程为方程组 F(x,y,z)=0 S2 (xy,z)=0F(x,y,=0 G(x,y,z)=0 例如,方程组 x2+y2=1 2x+3z=6 表示圆柱面与平面的交线C:
空间曲线可视为两曲面的交线, 其一般方程为方程组 例如,方程组 表示圆柱面与平面的交线C. S2 L G(x, y,z) = 0 F(x, y,z) = 0 S1 x z 1 y o C 2
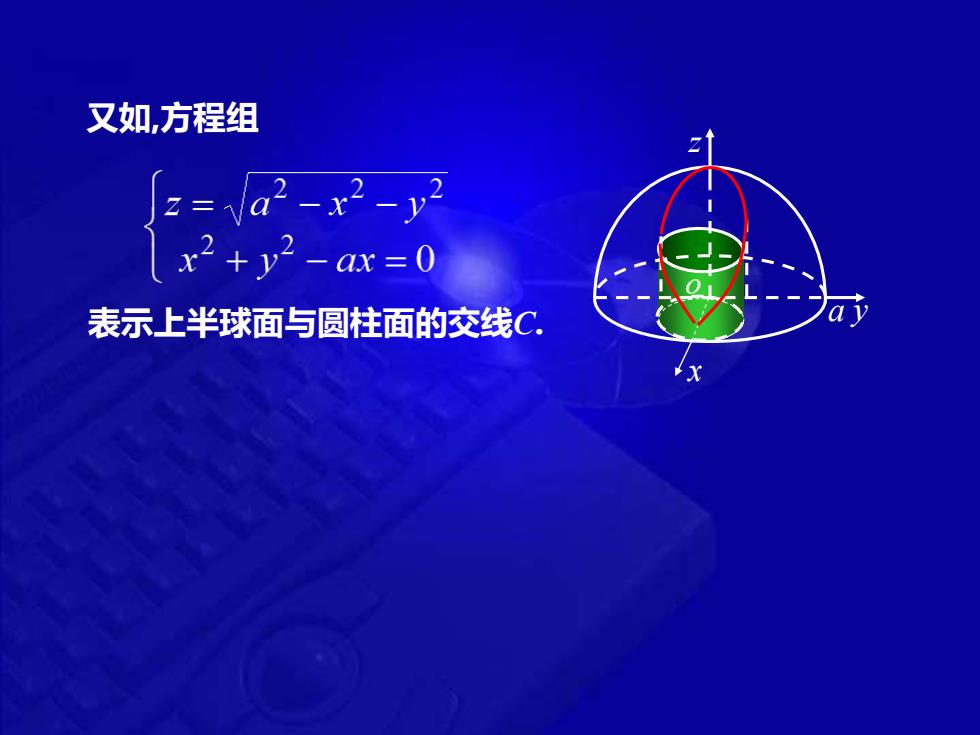
又如,方程组 表示上半球面与圆柱面的交线C
又如,方程组 表示上半球面与圆柱面的交线C. y x z a

空间曲线及其方程 空间曲线的一殷方程 二、空间曲线的参数方程 三、空间曲线在坐标面上的投影
空间曲线及其方程 一、空间曲线的一般方程 二、空间曲线的参数方程 三、空间曲线在坐标面上的投影

空间曲线及其方程 空间曲线的一殷方程 二、 空间曲线的参数方程 三、空间曲线在坐标面上的投影
空间曲线及其方程 一、空间曲线的一般方程 二、空间曲线的参数方程 三、空间曲线在坐标面上的投影

将曲线C上的动点坐标x,y,z表示成参数的函数: x=x(t) y=y(t) Z=z(t) 称为空间曲线的参数方程 例如,圆柱螺旋线的参数方程为 x=acos01令0=ot,b=y x=acos0 y=asinot V= asin z=vt z=b0 当0=2π时,上升高度h=2πb,称为螺距
z x y o 将曲线C上的动点坐标x,y,z表示成参数t的函数: 称为空间曲线的参数方程. v 令 = t , b = h = 2 b 例如,圆柱螺旋线 的参数方程为 上升高度 ,称为螺距 . M

◆例1将下列曲线化为参数方程表示: x2+y2=1 z=a2-x2-y2 2x+3z=6 +y2-ax=0 解:(1)根据第一方程引入参数,得所求为 x=coSt y=sint (0≤t≤2π) z=(6-2c0st) 2)将第二方程变形为(x-)2+y子=, 故所求为 (x=号+号cost y=sint (0≤t≤2π) 2=a2- cost
将下列曲线化为参数方程表示: 解: (1) 根据第一方程引入参数, (2) 将第二方程变形为 故所求为 得所求为 ◆例1

x=(t) ◆例2 求空间曲线T:y= w(t) (≤t≤阝)绕轴旋转 z=@(t) 时的旋转曲面方程. 解:任取点M1(p(t),W),o(t)eT,点M绕轴旋转, 转过角度后到点M(x,y,z),则 x=√0(t)+y2(t)cos0 a≤t≤B y=vo2()+w2(t)sin0 0≤0≤2π z=0(t) 这就是旋转曲面满足的参数方程
求空间曲线: 绕z轴旋转 时的旋转曲面方程 . 解: ( ( ), ( ), ( )) , 任取点M1 t t t 点M1绕z轴旋转, 转过角度后到点 则 这就是旋转曲面满足的参数方程 . ◆例2