《线性代数》课程PPT教学课件（B）第五章 相似矩阵与二次型_5-2特征值与特征向量

§5.2方阵的特征值与特征向量 一、特征值与特征向量的概念 二、特征值与特征向量的求法 三、特征值与特征向量的性质

§5.2 方阵的特征值与特征向量 一、特征值与特征向量的概念 二、特征值与特征向量的求法 三、特征值与特征向量的性质

一、方阵的特征值与特征向量的概念 定义5.2.1设A是n阶矩阵，若存在实数入和非零向 量x,使得Ax=几x成立，则称数2为方阵A的特征 值，非零向量x称为A的对应于特征值2的特征向量， 说明： 1.特征向量X。≠O列向量，并且满足AX。=X。 2.一个特征值有无穷多个特征向量，一个特征向量 只对应一个特征值 3.阶方阵A的特征值台A-E=0的根

5.2.1 , . A n x Ax x A x A     = 设 是 阶矩阵，若存在实数 和非零向 量 使得 成立，则称数 为方阵 的 非零向量 称为 的对应于特 特 征值 的 征 值， 特 定 征向量 义 一、方阵的特征值与特征向量的概念 说明： . 2. , 只对应一个特征值 一个特征值有无穷多个特征向量 一个特征向量 1. , . 特征向量X0  O列向量 并且满足AX0 = 0 X0 3.n阶方阵A的特征值 A−E = 0的根

由定义5.2.1得A-2E=0 12 n W 02- =0 。 上述行列式为关于的n次多项式，称A-E=0为 方阵A的特征方程 A-E是的n次多项式，称为方阵A的特征多项式， 记f4(2)=A-E

由定义5.2.1 0 得 A E − =  11 12 1 21 22 2 1 2 0 n n n n nn a a a a a a a a a    − −  = − . , 0 方阵 的特征方程 上述行列式为关于 的 次多项式 称 为 A  n A− E = ( ) . , , f A E A E n A A     = − − 记 是 的 次多项式 称为方阵 的特征多项式

4.方阵A的对应于的特征向量台方程组(A-E)X =0的任意非零解 二、特征值与特征向量求法 1.求特征值与特征向量的步骤： ()计算行列式A-2E=0,求出2的值，即为方阵A的 特征值 (2)求出(A-E)X=0的一个基础解系5，.，5n,则 特征值的所有特征向量为5=k气+.+k-,5m 其中k,.,k,-为不全为零的常数

0 . 4. ( ) 的任意非零解 方阵 的对应于 的特征向量 方程组 = A   A− E X 二、特征值与特征向量求法 1.求特征值与特征向量的步骤： . (1) 0, , 特征值 计算行列式 A− E = 求出的值 即为方阵A的 . (2) ( ) 0 , , , 1 1 1 n r n r n r k k A E X − − − = + + − =          特征值 的所有特征向量为 求出 的一个基础解系 则 , , . 其中k1  kn−r 为不全为零的常数

2.方阵特征值与特征向量的求解 3-1 例1求方阵A= 的特征值和特征向量 -13 解：A的特征多项式为 14-= 3- ，-1 -13- =(4-2)(2-2) 三的特征值为2=2,22=4 下边求特征向量（解(A-2E)X=O) 对21=2

   − − − − − = 1 3 3 1 A E 3 1 1 1 3 A   − =     − 例 求方阵 的特征值和特征向量 = (4 − )(2 − ) 1 2  = = A的特征值为  2, 4 2, 对1 = 下边求特征向量( ) 解( ) A E X O − = 2 解：A的特征多项式为 2.方阵特征值与特征向量的求解

3-2 (A-2E)x= 网 -13 →基础解系：p=(1,1)', ∴.P1=(1,1)'为属于特征值2的一个特征向量， 其全部特征向量为p1(k≠0)； 同理可求属于22=4的一个特征向量为P2=(-1,1)', 其全部特征向量为知2(k≠0)

2 2 同理可求属于 = = − 4 ( 1 1) , 的一个特征向量为 p ，  ( 0). 其全部特征向量为kp2 k  0 ; 其全部特征向量为kp1 （k  ） 1  = 基础解系: (1 1) p ，  ， 1  = p (1, 1) 2 , 为属于特征值 的一个特征向量 1 2 1 1 1 1 x x   −   =      −   1 2 1 1 0 0 0 x x   −     =      即 1 2 3 2 1 ( 2 ) 1 3 2 x A E x x   − −   − =      − −  

-1 1 0 例2求矩阵A= -4 30的特征值和特征向量 1 02 解 A的特征多项式为 -1-九 1 0 A-AE= -4 3-元 0 =(2-2)1-)2, 1 02-2 所以A的特征值为九1=2,22=23=1

1 1 0 2 . 4 3 0 1 0 2 A   −   = −       例 求矩阵 的特征值和特征向量 解 2 1 1 0 4 3 0 (2 )(1 ) , 1 0 2 A A E       − − − = − − = − − − 的特征多项式为 2, 1. 所以A的特征值为1 = 2 = 3 =

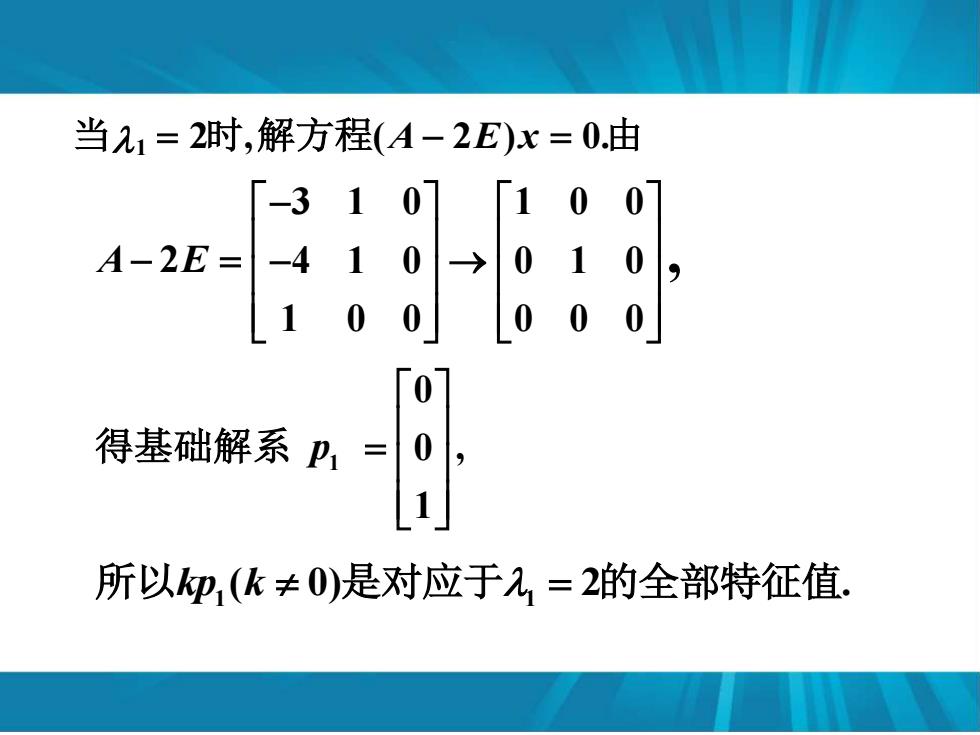
当1=2时，解方程(A-2E)x=0.由 -31 0 100 A-2E= -410 >01 0 100 000 0 得基础解系 p1= 0 所以仰，(k≠0)是对应于2=2的全部特征值

3 1 0 1 0 0 2 4 1 0 0 1 0 1 0 0 0 0 0 A E ,     −     − = → −             1 0 , 0 1 p     =       得基础解系 1 1 所以kp k( 0) 2 .  = 是对应于 的全部特征值 当1 = 2时,解方程(A − 2E)x = 0.由

当2=λ3=1时，解方程(A-E)x=0.由 -2 1 F10 1 A-E= -4 2 0 01 2 1 01 0 0 0 -1 得基础解系 P2= -2 1 所以仰，(k≠0)是对应于22=2=1的全部特征值

2 1 2 , 1 p   −   = −       得基础解系 2 2 3 所以kp k( 0) 1 .  = = 是对应于  的全部特征值 当2 = 3 = 1时,解方程(A − E)x = 0.由 2 1 0 1 0 1 4 2 0 0 1 2 , 1 0 1 0 0 0 A E     −     − = → −            

-2 117 例3求方阵A= 02 0的特征值和特征向量， -413 解A的特征多项式为 -2-λ 1 1 |A-元E= 0 2-元 0 一4 13- =-(2+10(2-2)2, 解得4的特征值为2=-1,22=23=2

解 2 1 1 0 2 0 4 1 3 A A E     − − − = − − − 的特征多项式为 ( 1)( 2) , 2 = −  +  − 1 2 3 解得A的特征值为   = − = = 1, 2. 2 1 1 3 0 2 0 4 1 3 A   −   =       − 例 求方阵 的特征值和特征向量