《线性代数》课程PPT教学课件（B）第五章 相似矩阵与二次型_5-1内积与正交向量

第五章相似矩阵与二次型 §5.1向量的内积与正交向量组 §5.2方阵的特征值与特征向量 §5.3相似矩阵 §5.4实对称矩阵的相似对角形 §5.5二次型及其标准型 §5.6正定二次型

第五章 相似矩阵与二次型 §5.1 向量的内积与正交向量组 §5.2 方阵的特征值与特征向量 §5.3 相似矩阵 §5.4 实对称矩阵的相似对角形 §5.5 二次型及其标准型 §5.6 正定二次型

§5.1向量的内积及正交向量组 一、内积的定义及性质 二、向量的长度及性质 三、正交向量组的概念及求法 四、正交矩阵与正交变换 五、小结思考题

§5.1 向量的内积及正交向量组 一、内积的定义及性质 二、向量的长度及性质 三、正交向量组的概念及求法 四、正交矩阵与正交变换 五、小结 思考题

一、内积的定义及性质 1.定义：设有n维向量 a d= an 令[a,B]=a,b+ab2+.+abn 则称a,B]为向量a与B的内积。 (1)n(n≥4)维向量的内积是三维向量数量积的推广， 但是没有3维向量的直观的几何意义. (2)向量内积可利用矩阵乘积表示（α，B为列向量时）

一、内积的定义及性质 1.定义：设有n维向量               n bn b b a a a   2 1 2 1  ,    n n  a b  a b  a b 1 1 2 2 令 ,  则称,  为向量与的内积。 (2)向量内积可利用矩阵乘积表示(,为列向量时) 3 . (1) ( 4) , 但是没有 维向量的直观的几何意义 n n  维向量的内积是三维向量数量积的推广

la,B]=aTB 内积的运算性质 (其中a,B,y为n维向量，2为实数)： ()[a,B]=[B,a] (2)[a,B]=元[a,B]; (3)[a+B,y]=[a,y]+[B,y]; (4)[a,]≥0，且当a≠0时有[a,a>0. schwarz不等式Ia,B]≤[a,a[B,B]

内积的运算性质 其中, , 为n维向量,为实数 : (1) ,     , ; (2)  ,      ,  ; (3)    ,    ,    , ; (4) [ , ]  0,且当  0时有[ , ]  0. 2 schwarz不等式 [,  ]  [,][ ,  ]      T , 

二、向量的长度及性质 定义5.1.2非负数V[a,a]=Va++.+a称为向量 a的长度（或范数），记作a· 向量的长度具有下述性质： 1.非负性当a≠0时，a>0;当a=0时，a=0 2.齐次性aal=la 3.三角不等式la+Bl≤la+

定义5.1.2   2 2 2 1 2 , . n   a a a   非负数    称 长度(或范数 量 的 ) 为向 ，记作 向量的长度具有下述性质： 1.非负性 当  0时,   0;当  0时,   0; 2. 齐次性     ; 3. 三角不等式        . 二、向量的长度及性质

当az=1时，称a为单位向量， 如果α≠0，有长度的概念得1 a就是一个单位向量 用非零数 去乘以向量a得到一个与a同方向的 单位向量，通常称为把向量单位化

当   1时,称 为单位向量. 1  0,  .  如果  有长度的概念得 就是一个单位向量 1 .     用非零数 去乘以向量 得到一个与 同方向的 单位向量，通常称为把向量 单位化

三、正交向量组的概念及求法 1.当，B]=0,称向量，B正交 说明：零向量与任意一个向量正交，并且只有零向量 与其自身正交。 定义5.1.3一组两两正交的非零向量称为正交向量组。 若正交向量组中每个向量都是单位向量，则称该向量组 为标准正交向量组. 说明：标准正交向量组也是正交向量组. 定理5.1.1正交向量组是线性无关向量组

三、正交向量组的概念及求法 1.当,   0,称向量,正交. 与其自身正交。 说明:零向量与任意一个向量正交,并且只有零向量 定义5.1.3 一组两两正交的非零向量称为正交向量组。 若正交向量组中每个向量都是单位向量,则称该向量组 为标准正交向量组. 定理5.1.1 正交向量组是线性无关向量组. 说明:标准正交向量组也是正交向量组

证明设有a1,a2,anm是正交向量组，若有 k1c1+k2C2+.+knm&m=0 用α，与等式两边做内积，得 k[a,a]=0i=1,2,.,m 由a≠0，有[a,a,>0,从而得 k=0i=1,2,.,m. 故c1,C2,.,Cm线性无关

证明 1 1 2 2 0 m m k   k   k   , i 用a 与等式两边做内积 得 1 2 , , , 设有    m 是正交向量组，若有 [ , ] 0 1,2, , i i i k    i   m 0, [ , ] 0, 由i  有 i i  从而得 0 1, 2, , . i k  i   m 1 2 , , , . 故    m线性无关

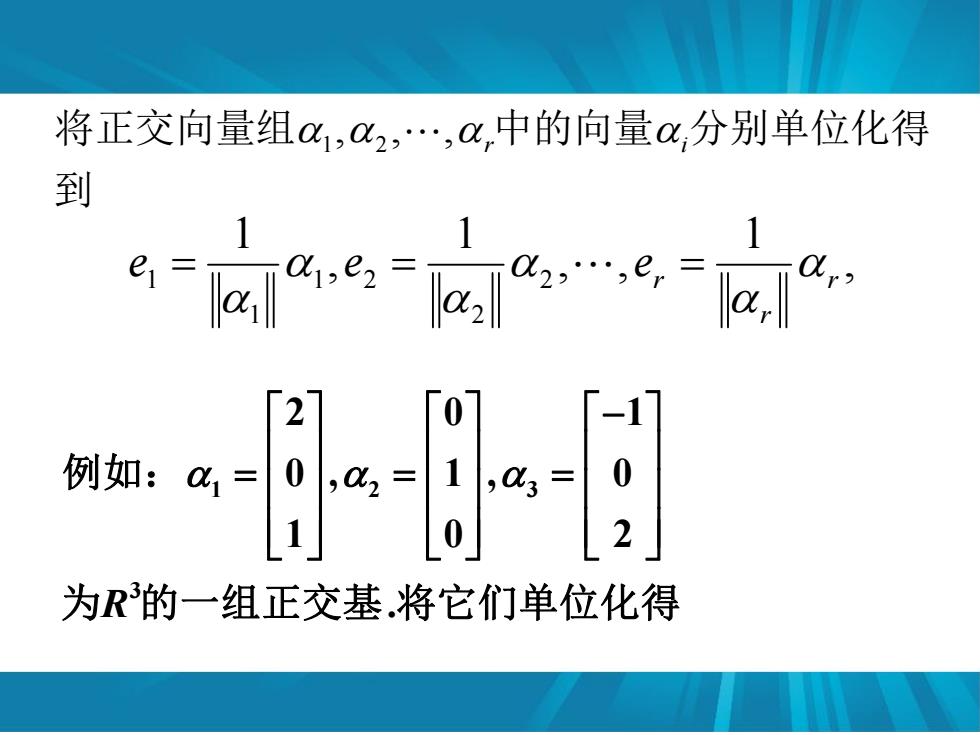
将正交向量组1,02，.，C,中的向量x,分别单位化得 到 2 0 -1 例如：a1=0,a2=1 ,C3= 0 1 2 为R的一组正交基.将它们单位化得

1 2 3 3 2 0 1 0 , 1 , 0 1 0 2 R .                                     例如： 为 的一组正交基 将它们单位化得 到 将正交向量组1 , 2 ,, r中的向量i分别单位化得 , 1 , , 1 , 1 2 2 1 2 1 1 r r r e e e          

2 0 -1 1 e 5 0,2= 1 0 1 0 2 所以e1,e2,e3为R的一个标准正交基

1 2 3 2 0 1 1 1 0 , 1 , 0 5 5 1 0 2 e e e                                  3 1 2 3 所以 e , e , e 为R 的一个标准正交基