
§3.2 Relation Calculus(关系运算 Relation calculus: 1.Relation Algebra; 2.Tuple Relational Calculus; 3.Domain Relational Calculus ?们是DML语言的基础,可以证明三 种关系运算具有同等表达能力。 48
48 §3.2Relation Calculus(关系运算) Relation calculus: 1.Relation Algebra; 2.Tuple Relational Calculus; 3.Domain Relational Calculus ; 它们是DML语言的基础, 可以证明三 种关系运算具有同等表达能力

一.Relation Algebra(关系代数) 规定 关系R属性: A1,A2,...AK; 可用属性名,也可用它们的序号 表示,还可以把任一属性值称为该 元组的元组分量 49
49 一 .Relation Algebra(关系代数) 规定: 关系 R 属性: A1,A2,…,AK; 可用属性名,也可用它们的序号 表示,还可以把任一属性值称为该 元组的元组分量

·使用集合运算符,运算符优先权如下 ∈,一一 算数比较运算符 2 3 ∧ 4 V 5 。tuple variable 。 关系是元组的集合 50
50 • 使用集合运算符, 运算符优先权如下: ∈,-----------1 算数比较运算符 ---2 -------------3 -------------4 -------------5 • tuple variable • 关系是元组的集合

l,Union合并运算 设有同类关系R1,R2,定义二者合并运算: R1UR2=[tt∈R1Vt∈R2] 其中①U-Union Operator ②t-tuple Variable 含义①R1,R2元组的并集 ②R1,R2必须为同类关系,结果关系亦 为R1,R2的同类关系。 ③R1,R2有相等元组,结果关系中,只 出现一次。 51
51 1.Union 合并运算 设有同类关系R1,R2,定义二者合并运算: - R1 ∪ R2=[t|t∈R1t∈R2] 其中①U-Union Operator ②t-tuple Variable 含义①R1,R2元组的并集 ②R1,R2必须为同类关系,结果关系亦 为R1,R2的同类关系。 ③R1,R2有相等元组,结果关系中,只 出现一次
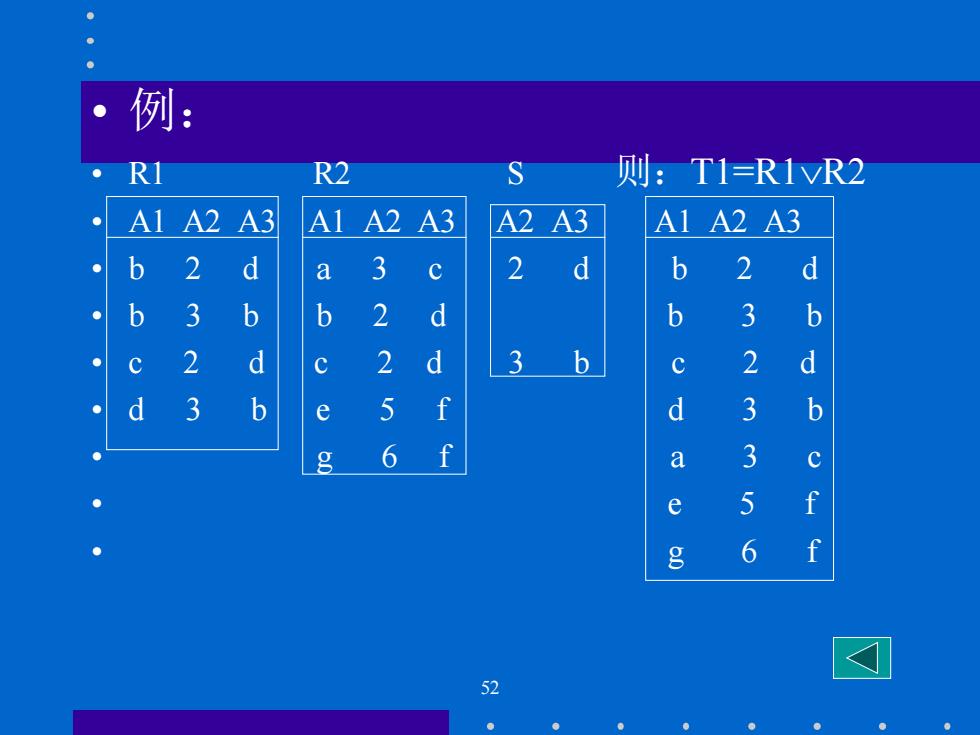
例: R1 R2 S 则:T1=R1R2 A1 A2 A3 A1 A2 A3 A2 A3 A1 A2 A3 b 2 d a 3 2 d b 2 d ● b 3 b b 2 d b 3 b c 2 d c 2 d 3 b c 2 d d 3 b e 5 f d b g 6 f a 3 c 5 f g 6 52
52 • 例: • R1 R2 S 则:T1=R1R2 • A1 A2 A3 A1 A2 A3 A2 A3 A1 A2 A3 • b 2 d a 3 c 2 d b 2 d • b 3 b b 2 d b 3 b • c 2 d c 2 d 3 b c 2 d • d 3 b e 5 f d 3 b • g 6 f a 3 c • e 5 f • g 6 f
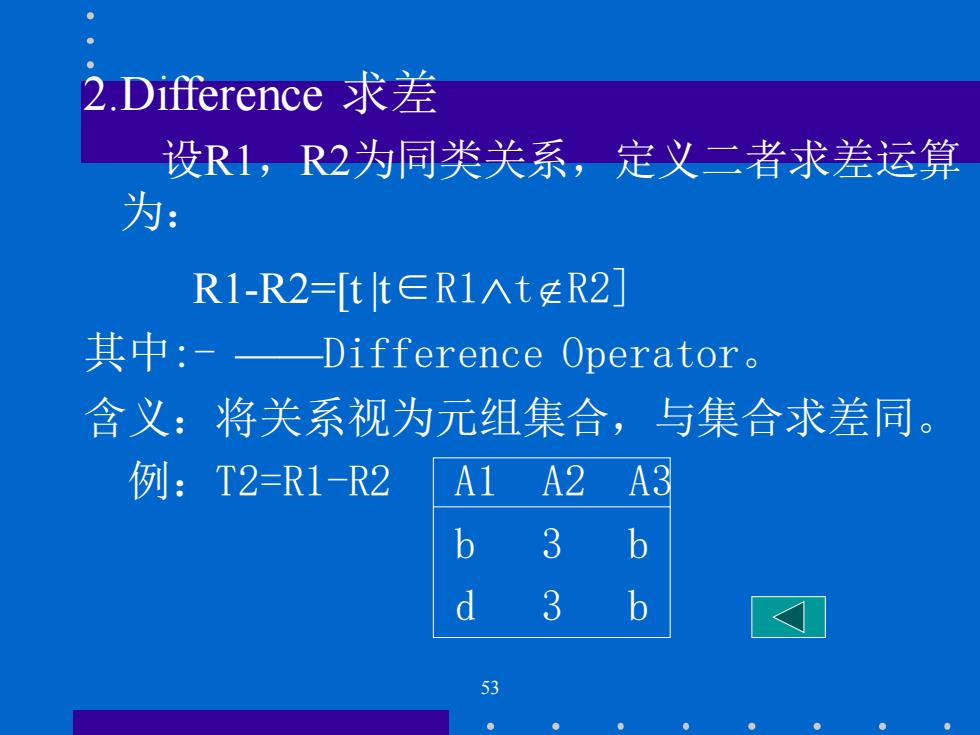
2.Difference求差 设R1,R2为同类关系,定义二者求差运算 为: R1-R2=[tt∈R1入teR2] 其中:-—Difference Operator。 含义:将关系视为元组集合,与集合求差同。 例:T2=R1-R2 A1 A2 A3 b 3 b d 3 53
53 2.Difference 求差 设R1,R2为同类关系,定义二者求差运算 为: R1-R2=[t |t∈R1tR2] 其中:- ——Difference Operator。 含义:将关系视为元组集合,与集合求差同。 例:T2=R1-R2 A1 A2 A3 b 3 b d 3 b

3 Product求积 设:R为K1度关系,S为K2度关系定义二者乘 积: RxS=[tt=Atk1∈RAtk2∈S] 其中:X-Product Operator 含义:设R有N1个元组,S有N2个元组,将 R,S分别视为N1,N2重有序组,RxS与两个 有序组笛卡尔积同意义。 54
54 3.Product 求积 设:R为K1度关系,S为K2度关系.定义二者乘 积: RS=[t|t=t k1∈R t k2 ∈S] 其中:X-Product Operator 含义:设R有N1个元组,S有N2个元组,将 R,S分别视为N1,N2重有序组,RS与两个 有序组笛卡尔积同意义
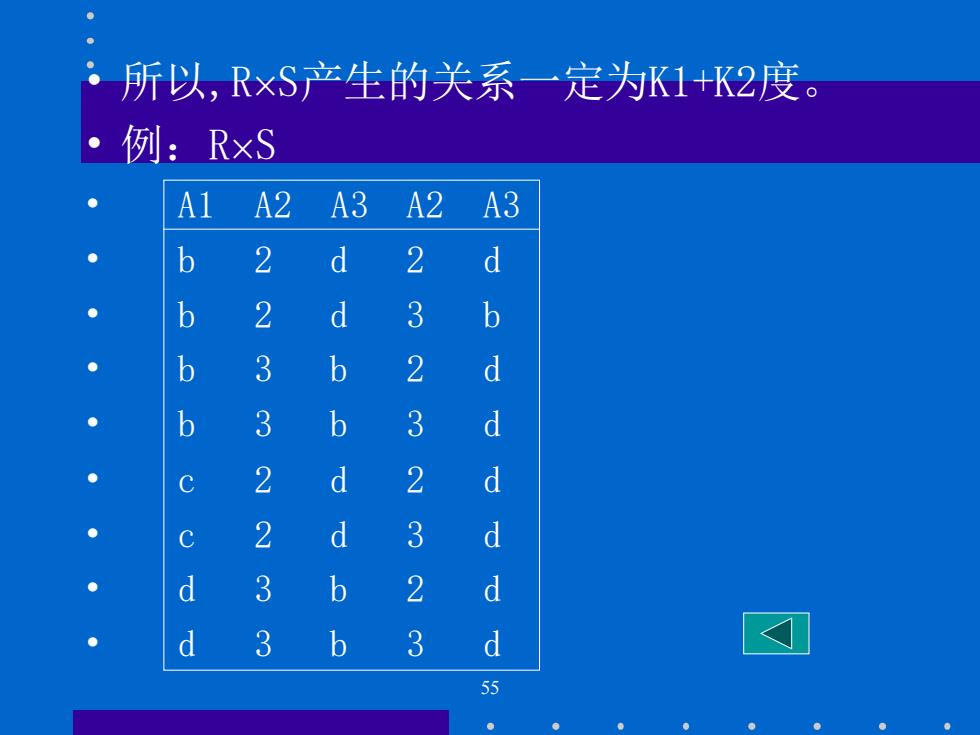
所以,RxS产生的关系一定为K1+K2度。 ·例:RxS A1 A2 A3 A2 A3 b 2 d b 2 3 b b 3 2 d b 3 3 d 2 d C 2 d 3 d d 3 b 2 d d 3 b 3 d 团 55
55 • 所以,RS产生的关系一定为K1+K2度。 • 例:RS • A1 A2 A3 A2 A3 • b 2 d 2 d • b 2 d 3 b • b 3 b 2 d • b 3 b 3 d • c 2 d 2 d • c 2 d 3 d • d 3 b 2 d • d 3 b 3 d

4.Projection投影 设有K度关系R,其元组变量为: tK=∧℃∧∈R] 56
56 4.Projection 投影 设有K度关系R,其元组变量为: t K=, 那么在关系R的分量: Aj1,Aj2,…,Ajn (其中nk, j1,j2,…,jn在1~k之间), 上的投影定义为: ∏j1,j2,…,jn(R)=[t|t= ∈R]

含义: 。 按j1,…jn的顺序,取下这N列,构成 的jl,.jn为列序的N度关系。 ·其中:Π—Projection Operator ·例:Π3,2(R A3 A2 d 2 b 3 可 57
57 • 含义: • 按j1,…,jn的顺序,取下这N列,构成 的j1,…,jn为列序的N度关系。 • 其中 :∏——Projection Operator • 例:∏3,2(R) • A3 A2 • d 2 • b 3