
SHONAN 别 NII MEETING Distributed Algorithms MCMp for Yitong Yin Nanjing University Shonan Meeting No.162:Distributed Graph Algorithms
Distributed Algorithms for MCMC Sampling Yitong Yin Nanjing University Shonan Meeting No. 162: Distributed Graph Algorithms

Outline Distributed Sampling Problem Gibbs Distribution (distribution defined by local constraints) Algorithmic ldeas CLocal Metropolis Algorithm LOCAL Jerrum-Valiant-Vazirani Local Rejection Sampling MCMC Distributed Simulation of Metropolis (with ideal parallelism) MCMC:Markoy chain Monte Carlo
Outline • Distributed Sampling Problem • Gibbs Distribution (distribution defined by local constraints) • Algorithmic Ideas • Local Metropolis Algorithm • LOCAL Jerrum-Valiant-Vazirani • Local Rejection Sampling • Distributed Simulation of Metropolis (with ideal parallelism) MCMC MCMC MCMC: Markov chain Monte Carlo
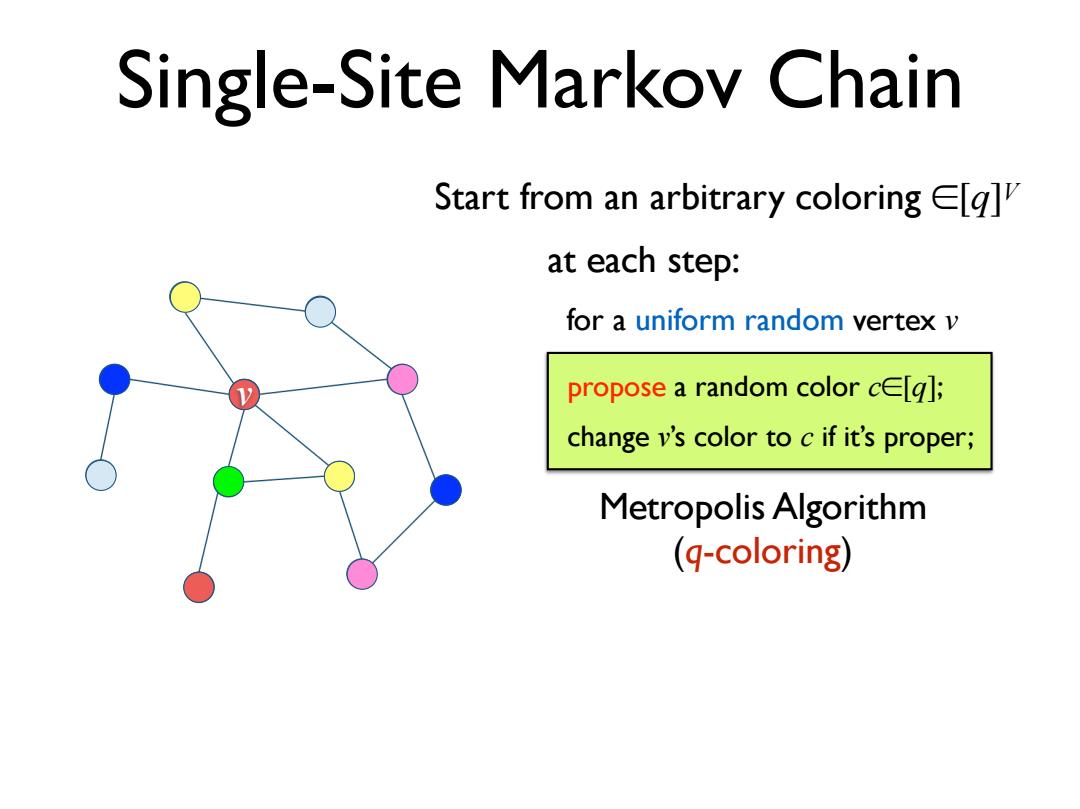
Single-Site Markov Chain Start from an arbitrary coloring Elg] at each step: for a uniform random vertex v propose a random color cE[g]; change v's color to c if it's proper; Metropolis Algorithm (q-coloring)
Single-Site Markov Chain v propose a random color c∈[q]; change v’s color to c if it’s proper; at each step: Metropolis Algorithm (q-coloring) for a uniform random vertex v Start from an arbitrary coloring ∈[q]V
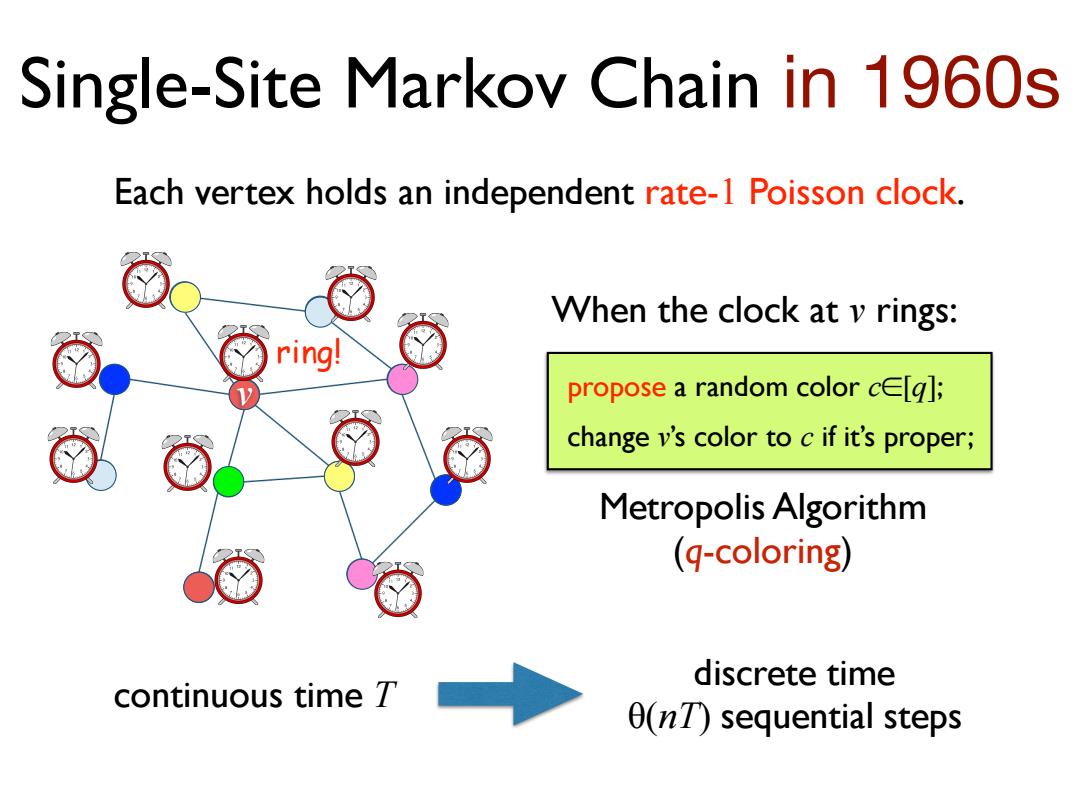
Single-Site Markov Chain in 1960s Each vertex holds an independent rate-1 Poisson clock. When the clock at v rings: ring! propose a random color ce[g]; change v's color to c if it's proper; Metropolis Algorithm (q-coloring) discrete time continuous time 7 0(nT)sequential steps
v propose a random color c∈[q]; change v’s color to c if it’s proper; Metropolis Algorithm (q-coloring) Single-Site Markov Chain in 1960s Each vertex holds an independent rate-1 Poisson clock. When the clock at v rings: continuous time T discrete time θ(nT) sequential steps ring!

Distributed Simulation of Continuous-Time Process Goal:Give a distributed algorithm that perfect simulates the time T continuous Markoy chain. (Have the same behavior given the same random bits.) do NOT allow adjacent vertices update their colors in the same round: O(7)rounds [Feng,Hayes,Y.'19]: O(T+log n)rounds w.h.p. (under some mild condition)
Distributed Simulation of Continuous-Time Process Goal: Give a distributed algorithm that perfect simulates the time T continuous Markov chain. (Have the same behavior given the same random bits.) do NOT allow adjacent vertices update their colors in the same round: O(ΔT) rounds [Feng, Hayes, Y. ’19]: O(T + log n) rounds w.h.p. (under some mild condition)

2-Phase Paradigm for each vertex v∈V: Phase l: .locally generate all update times 0<<<<tM <T and proposed colors c,C2,...,CM,e[q]; send the initial color and all (isM,to all neighbors; Phase ll: ● For i=1,2,...,My do: once having received enough information: resolve the i-th update of v and send the result ("Accept Reject")to all neighbors;
• locally generate all update times and proposed colors ; • send the initial color and all to all neighbors; 0 < t 1 < t 2 < ⋯ < t Mv < T c1, c2, …, cMv ∈ [q] (t i , ci )1≤i≤Mv Phase I: for each vertex v ∈ V: Phase II: • For do: once having received enough information: resolve the i-th update of v and send the result (“Accept / Reject”) to all neighbors; i = 1,2,…, Mv 2-Phase Paradigm
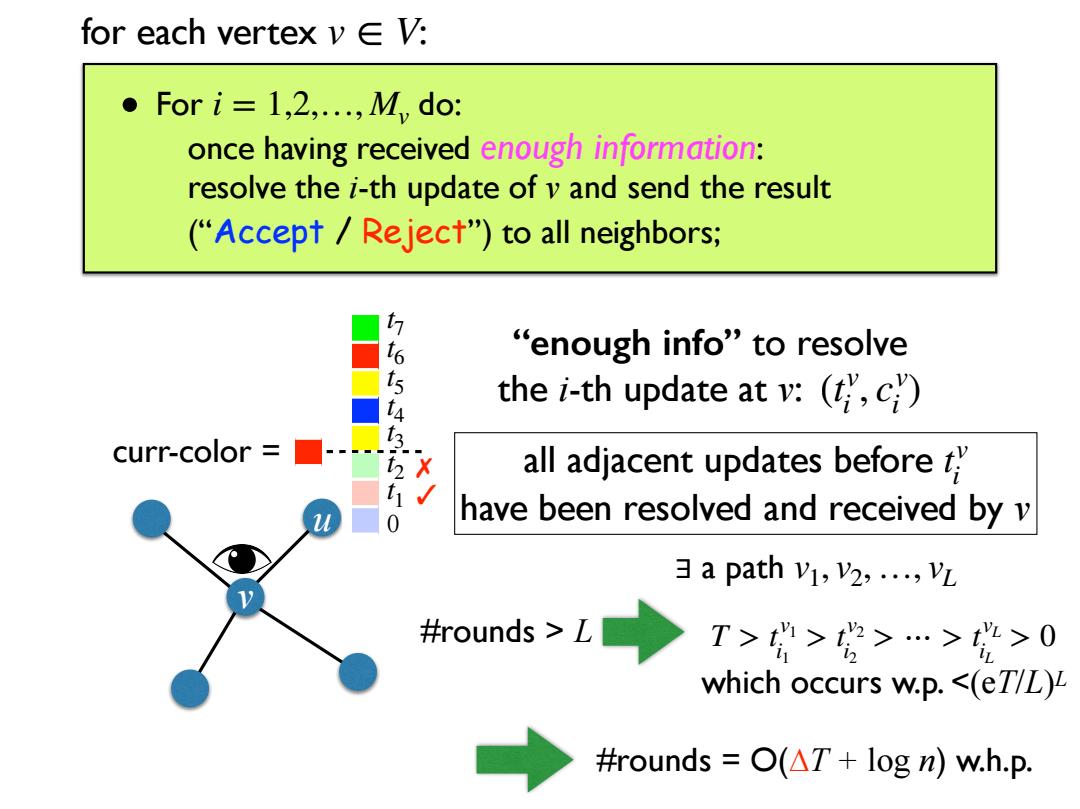
for each vertex v∈V: ● For i=1,2,...,M,do: once having received enough information: resolve the i-th update of v and send the result ("Accept Reject")to all neighbors; 6 "enough info"to resolve the i-th update at v:(c) 5 curr-color all adjacent updates before 0 have been resolved and received by v 3a path v1,v2,...,VL #rounds >L T>>安>…>丝>0 which occurs w.p.<(eT/L) #rounds =O(AT+log n)w.h.p
for each vertex v ∈ V: • For do: once having received enough information: resolve the i-th update of v and send the result (“Accept / Reject”) to all neighbors; i = 1,2,…, Mv v 0 t 1 t 2 t 3 t 4 t 5 t 6 t 7 u curr-color = “enough info” to resolve the i-th update at v: (t v i , cv i ) ✓ ✗ all adjacent updates before have been resolved and received by v t v i #rounds > L ∃ a path v1, v2, …, vL T > t v1 i1 > t v2 i2 > ⋯ > t vL iL > 0 which occurs w.p. <(eT/L)L #rounds = O(∆T + log n) w.h.p
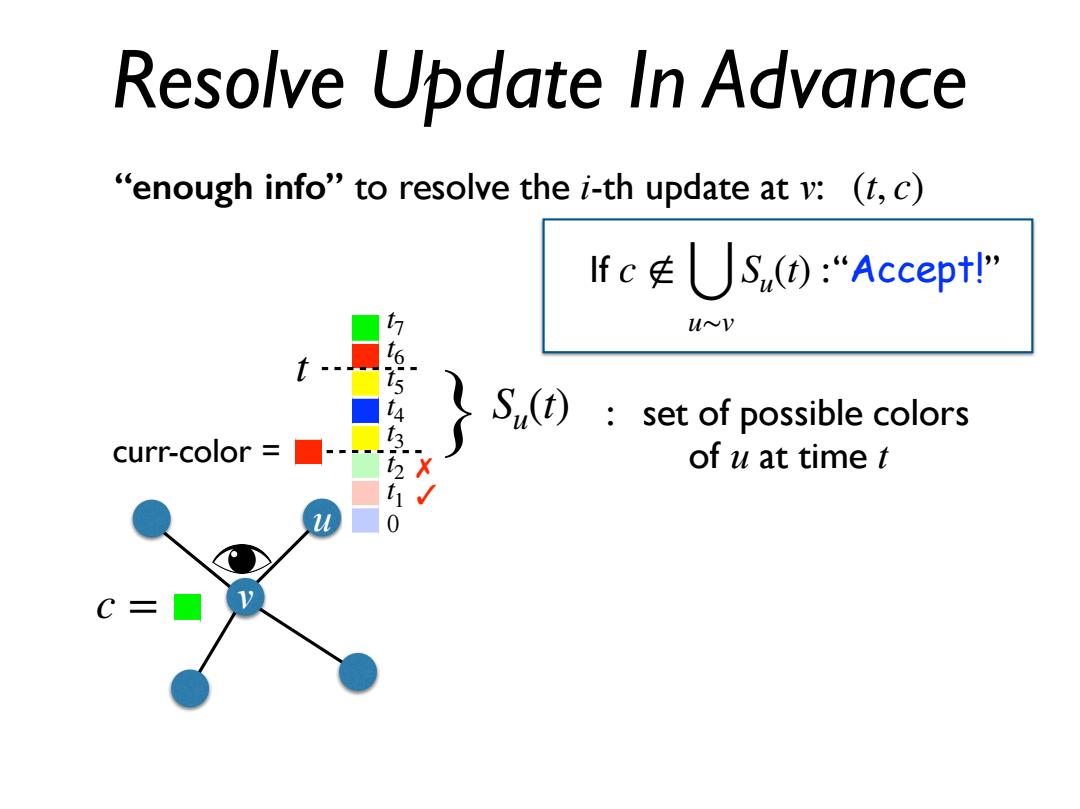
Resolve Update In Advance "enough info"to resolve the i-th update at v:(t,c) Ifc车US,(④:“Accept!" tn u~V S(t):set of possible colors curr-color X of u at time t 0
v 0 t 1 t 2 t 3 t 4 t 5 t 6 t 7 u curr-color = ✓ ✗ Resolve Update In Advance t “enough info” to resolve the i-th update at v: (t, c) } Su(t) If c ∉ ⋃ : “Accept!” u∼v Su(t) : set of possible colors of u at time t c =

Resolve Update In Advance "enough info"to resolve the i-th update at v:(t,c) Ifc车US,(④:“Accept!" UoV curr-color S(t):set of possible colors of u at time t 0 Ifuベvs.tS(t)={c}: “Reject!
v 0 t 1 t 2 t 3 t 4 t 5 t 6 t 7 u curr-color = ✓ ✓ Resolve Update In Advance } If : “Reject!” ∃u ∼ v s.t. Su(t) = {c} If c ∉ ⋃ : “Accept!” u∼v Su(t) “enough info” to resolve the i-th update at v: (t, c) Su(t) : set of possible colors of u at time t t c =
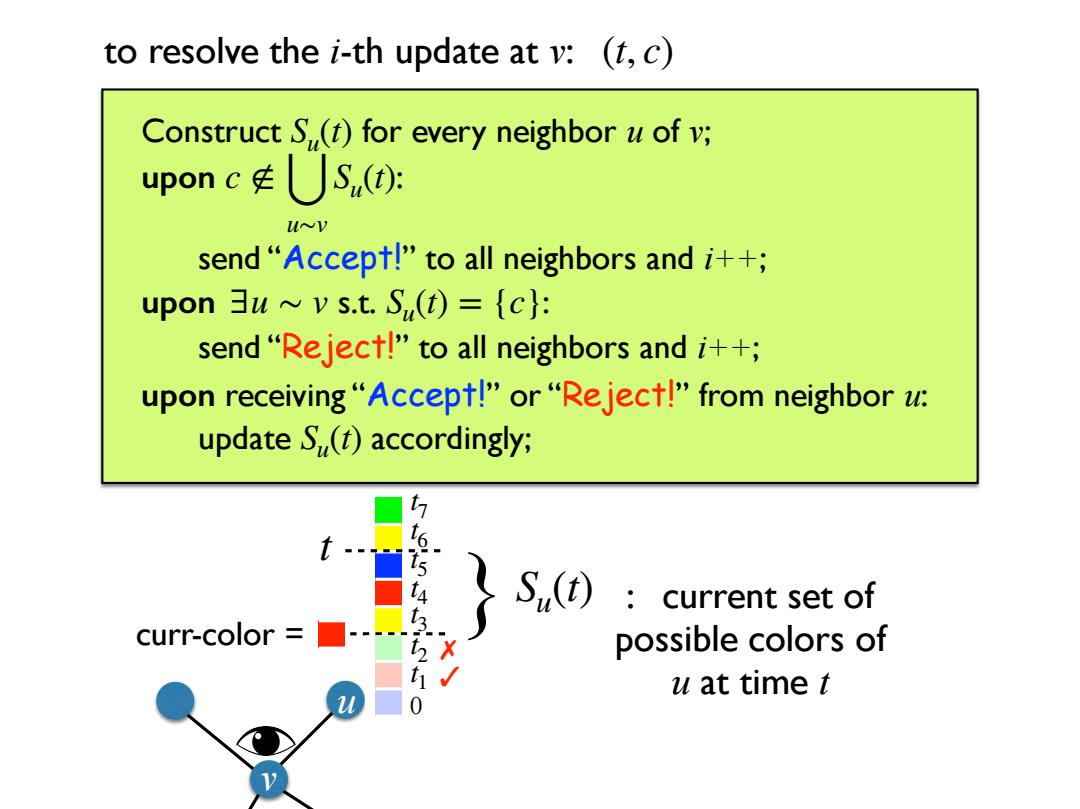
to resolve the i-th update at v:(t,c) Construct S(t)for every neighbor u of v; upon cS,(1): WoV send "Accept!"to all neighbors andi++; upon 3u~v s.t.S(t)={c}: send "Reject!"to all neighbors andi++; upon receiving"Accept!"or "Reject!"from neighbor u: update S(t)accordingly; t… S.(t) ):current set of curr-color possible colors of u at time t 0
Construct for every neighbor u of v; upon : send “Accept!” to all neighbors and i++; upon : send “Reject!” to all neighbors and i++; upon receiving “Accept!” or “Reject!” from neighbor u: update accordingly; Su(t) c ∉ ⋃ u∼v Su(t) ∃u ∼ v s.t. Su(t) = {c} Su(t) to resolve the i-th update at v: (t, c) v 0 t 1 t 2 t 3 t 4 t 5 t 6 t 7 u curr-color = ✓ ✗ t } Su(t) : current set of possible colors of u at time t