
5.5动态规划求解 0/1背包问题
5.5动态规划求解 0/1背包问题

1.问题描述 背包容量M,n个物品,分别具有效益值P1..Pn,物 品重量w1.wn,从n个物品中,选择若干物品放入 背包,物品要么整件放入背包,要么不放入。怎 样决策可以使装入背包的物品总效益值最大? 形式化描述: 目标函数: max ∑PX1 1si≤j 约束条件: ∑wX;≤M ≤i≤n x1=0或1,p1>0,w;>0,1≤i≤n 0/1背包问题:KNAP(1,n,M)
形式化描述: 目标函数: 约束条件: 0/1背包问题:KNAP(1,n,M) 1ij i i max p x x 0 1,p 0,w 0,1 i n w x M i i i 1 i n i i = 或 1.问题描述 背包容量M,n个物品,分别具有效益值P1…Pn,物 品重量w1…wn,从n个物品中,选择若干物品放入 背包,物品要么整件放入背包,要么不放入。怎 样决策可以使装入背包的物品总效益值最大?

÷0/1背包问题:M=6,N=3,W=(3,3,4),P=(3,3,5) 贪心法:p3w3>p1w1>p2w2 。贪心解 ∑P=5(0,0,1) ÷最优解是:∑P=6(1,1,0)
❖ 0/1背包问题:M=6,N=3,W=(3,3,4),P=(3,3,5) ❖ 贪心法:p3/w3 > p1/w1 > p2/w2 ❖ 贪心解 ∑P=5(0,0,1) ❖ 最优解是:∑P=6(1,1,0)

·贪心法求解0/1背包问题不一定得到最优解 ÷动态规划求解的问题必须满足最优化原理
❖ 贪心法求解0/1背包问题不一定得到最优解! ❖ 动态规划求解的问题必须满足最优化原理

2.最优化原理证明 设y1y2,yn是×1,X2,,Xn的0/1值最优序列。 若y1=0,KNAP(2,n,M)是初始决策产生的状态。则 y2yn相对于KNAP(2,n,M)将构成一个最优序列。否则, y1y2,yn将不是KNAP(1,n,M)的最优解 若y1=1,KNAP(2,n,M一w1)是初始决策产生的状态。 则y2yn相对于KNAP(2,n,M一w1)将构成一个最优序列。 否则,设存在另一0/1序列z1,Z2,乙n,使得∑w,2≤M-w 2≤i≤n 且 ∑p,,≥∑py 2≤i≤n 2≤i≤n 则序列y1,z2,,Zn将是一个对于KNAP(1,n,M)具有更大 效益值的序列。 故,最优性原理成立
设y1 ,y2 ,…,yn是x1 ,x2 ,…,xn的0/1值最优序列。 若y1=0, KNAP(2,n,M)是初始决策产生的状态。则 y2 ,…,yn相对于KNAP(2,n,M)将构成一个最优序列。否则, y1 ,y2 ,…,yn将不是KNAP(1,n,M)的最优解 若y1=1, KNAP(2,n,M-w1 )是初始决策产生的状态。 则y2 ,…,yn相对于KNAP(2,n,M-w1 )将构成一个最优序列。 否则,设存在另一0/1序列z1 ,z2 ,…,zn ,使得 且 则序列y1 ,z2 ,…,zn将是一个对于KNAP(1,n,M)具有更大 效益值的序列。 故,最优性原理成立 − i n wi zi M w 2 1 i n i n i i i i p z p y 2 2 2.最优化原理证明

3 从前向后求解的递推关系式 记f()是KNAP(1,jX)的最优解,则fnM) 是KNAP(1,n,M)的最优解 对于fn(M)有: fn(M)=maxffn-1(M),fn-1(M-Wn)+pn} 第N个物品不放入 第N个物品放入 Xn=0 Xn=1 对于任意的f(X),>0,有 fi(X)max{fi1(X),fi1(X-wi)+pi}
3 从前向后求解的递推关系式 记fj (X)是KNAP(1,j,X)的最优解,则fn (M) 是KNAP(1,n,M)的最优解 对于fn (M)有: fn (M) = max{fn-1 (M), fn-1 (M-wn )+pn } 对于任意的fi (X),i>0,有 fi (X) = max{fi-1 (X),fi-1 (X-wi )+pi } 第N个物品不放入 xn=0 第N个物品放入 xn=1

递推过程: ★初始值 0 X≥0 X<0 Af (X)=max {fo(X),fo(X-W)+P} 求出所有可能的X对应的f值 *fi(X)=max {fi-1(X),fi-1(X-Wi)+Pi} ★最后求fn(M)=KNAP(1,n,M)
递推过程: ★初始值 0 X≥0 f0(X)= -∞ X<0 ★f1(X)=max{f0(X),f0(X-W1)+P1} 求出所有可能的X对应的fi值 ★fi(X)=max{fi-1(X),fi-1(X-Wi)+Pi} ★最后求 fn (M)=KNAP(1,n,M)

f(X)=maxff1(X),f1(X-wi)+pi) 4例用动态规划法求解0/1背包问题 n=3,(W1,w2,w3)=(2,3,4),(p1,P2,P3)=(1,2,5),M=6 递推计算过程 {g X<0 X20 w=f X<0 max{0,一∞+1}=0 0≤X<2 max{0,0+1}=1 X22 X<0 0 0≤X<2 f2(X)=〈1 2≤X<3 max{1,0+2}=2 3≤X<5 max{1,1+2}=3 X25 f3(M)=max3,1+5)=6
4例用动态规划法求解0/1背包问题 n=3,(w1 ,w2 ,w3 )=(2,3,4),(p1 ,p2 ,p3 )=(1,2,5),M=6 递推计算过程 -∞ X<0 f0 (X)= 0 X≥0 -∞ X<0 max{0,-∞+1}=0 0≤X<2 max{0,0+1} = 1 X≥2 -∞ X<0 0 0≤X<2 1 2≤X<3 max{1,0+2}=2 3≤X<5 max{1,1+2} = 3 X≥5 f3 (M)= max{3,1+5} = 6 fi (X) = max{fi-1 (X),fi-1 (X-wi)+pi} f1(X)= f2(X)=
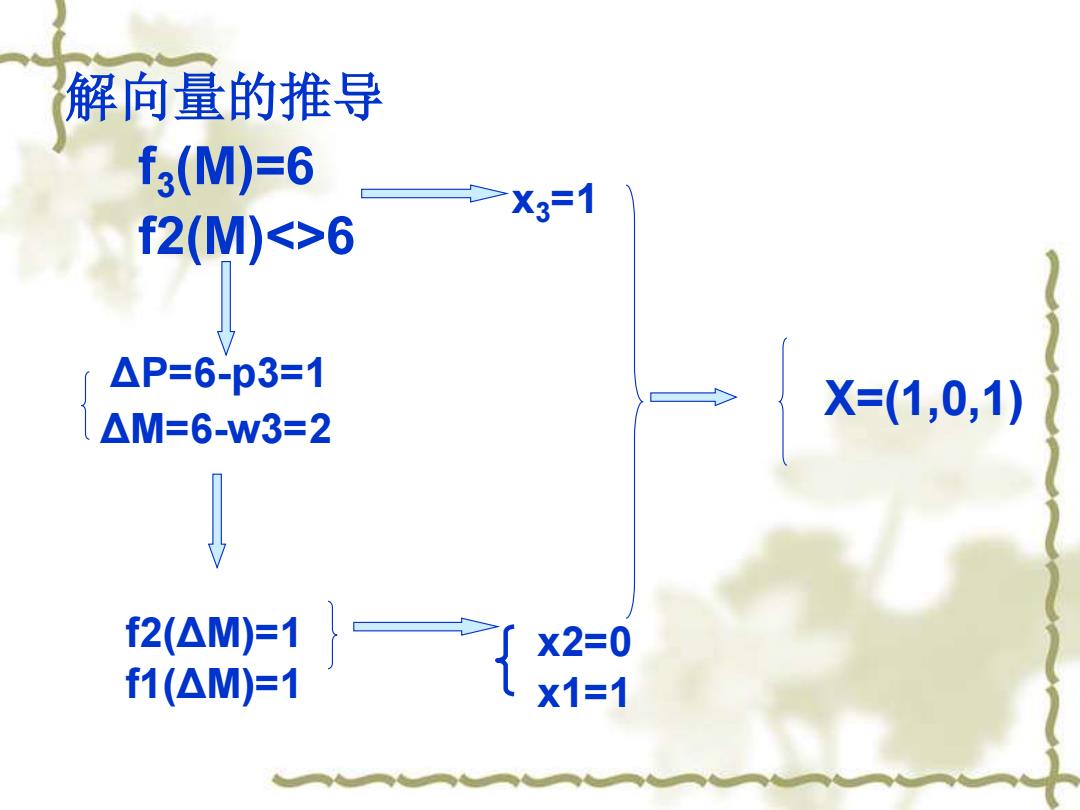
解向量的推导 f3(M)=6 >X3=1 f2(M)<>6 △P=6-p3=1 X=(1,0,1) △M=6-w3=2 f2(△M)=1 X2=0 f1(△M)=1 X1=1
解向量的推导 f3 (M)=6 f2(M)<>6 x3=1 ΔP=6-p3=1 ΔM=6-w3=2 X=(1,0,1) f2(ΔM)=1 f1(ΔM)=1 x2=0 x1=1

5.0/1背包问题图解过程 (x) fo(x)=0 if.(X-w)+p1 =0:函数不存在 01234567X i=1:fo(X-W1)+p1 2 f(x) 2 01234567X 01234567x i=2:f1(X-w2)+p2 3 f2(x) 32 01234567X 01234567X
5. 0/1背包问题图解过程 i:fi-1 (x-wi ) + pi i=0:函数不存在 0 1 2 3 4 5 6 7 1 2 i=1:f0 (x-w1 ) + p1 x 0 1 2 3 4 5 6 7 1 2 i=2:f1 (x-w2 ) + p2 3 x 0 1 2 3 4 5 6 7 1 2 f1 (x) x 0 1 2 3 4 5 6 7 1 2 3 x f2 (x) 0 1 2 3 4 5 6 7 1 2 f0 (x)=0 x fi (x)