
递归及递归算法 分析
1 递归及递归算法 分析

主要内容 递归的实现机制 递归算法编制 递归关系式求解
2 主要内容 ❖ 递归的实现机制 ❖ 递归算法编制 ❖ 递归关系式求解

递归的实现机制 1.递割归的概念 直接或间接地调用自身的算法称为递归算 法。 冬用函数自身给出定义的函数称为递归函数。 直接调用自身的算法称为直接递归 间接调用自身的算法称为间接递归
3 递归的实现机制 1.递归的概念 ❖ 直接或间接地调用自身的算法称为递归算 法。 ❖ 用函数自身给出定义的函数称为递归函数。 ❖ 直接调用自身的算法称为直接递归 ❖ 间接调用自身的算法称为间接递归

由分治法产生的子问题往往是原问题的较小 模式,这就为使用递归技术提供了方便。在 这种情况下,反复应用分治手段,可以使子 问题与原问题类型一致而其规模却不断缩小 最终使子问题缩小到很容易直接求出其解。 这自然导致递归过程的产生。 分治与递归像一对孪生兄弟, 经常同时应用 在算法设计之中,并由此产生许多高效算法
4 ❖ 由分治法产生的子问题往往是原问题的较小 模式,这就为使用递归技术提供了方便。在 这种情况下,反复应用分治手段,可以使子 问题与原问题类型一致而其规模却不断缩小, 最终使子问题缩小到很容易直接求出其解。 这自然导致递归过程的产生。 ❖ 分治与递归像一对孪生兄弟,经常同时应用 在算法设计之中,并由此产生许多高效算法
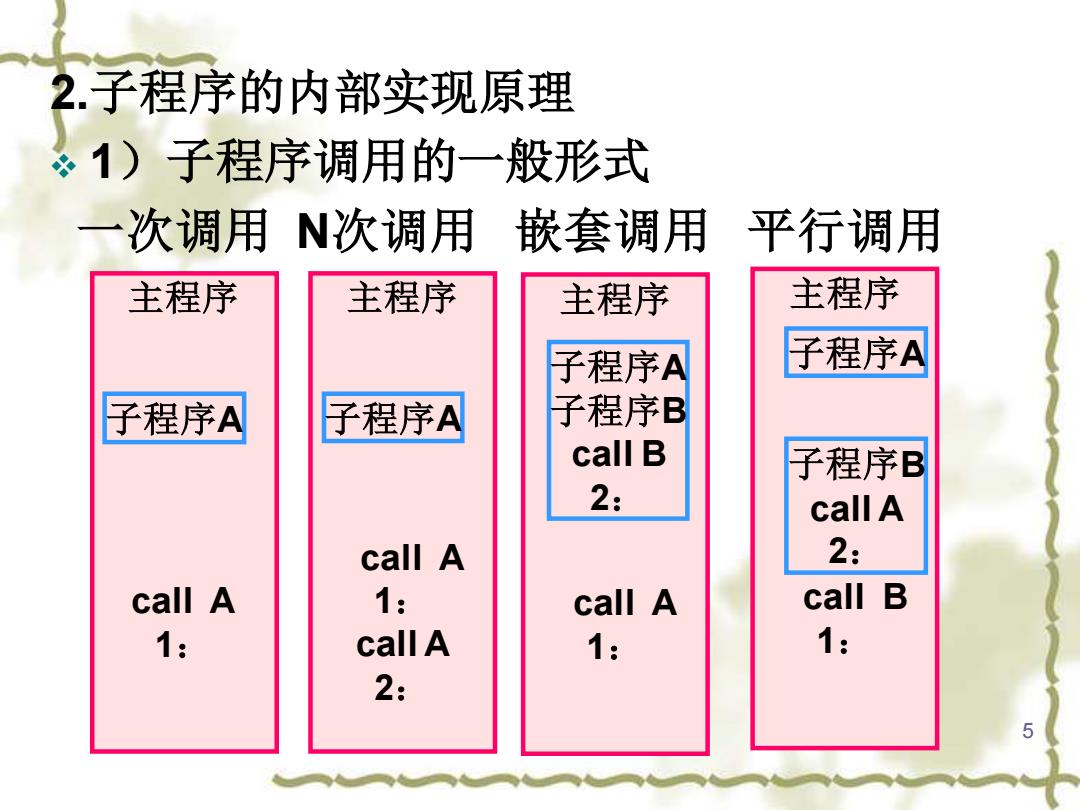
2.子程序的内部实现原理 。1)子程序调用的一般形式 一次调用N次调用嵌套调用 平行调用 主程序 主程序 主程序 主程序 子程序A 子程序A 子程序A 子程序A 子程序B call B 子程序B 2: call A call A 2: call A 1: call A call B 1: call A 1: 1: 2:
5 主程序 call A 1: 2.子程序的内部实现原理 ❖ 1)子程序调用的一般形式 一次调用 N次调用 嵌套调用 平行调用 子程序A 主程序 call A 1: call A 2: 子程序A 主程序 call A 1: 子程序A 子程序B call B 2: 主程序 call B 1: 子程序B call A 2: 子程序A

82)值的回传 1 。实参和形参的数据传递 实参 变参 ó传值实参的值不发生改变 6传地址实参的值发生改变 地址X 2 实参 变参 值的回传通常有两种形式: X 6两次传值方式:按照指定类型为变参设置相应的 存储空间,在执行调用时,将实参值传送给变参 在返回时将变参的值传给实参。 6传地址:在内部将变参用一个地址替换,调用时 先执行地址传送,将实参地址传送给变参,在执 行过程中,对变参的操作实际变成对实参的操作
6 ❖ 2)值的回传 ❖ 实参和形参的数据传递 传值 实参的值不发生改变 传地址 实参的值发生改变 ❖ 值的回传通常有两种形式: 两次传值方式:按照指定类型为变参设置相应的 存储空间,在执行调用时,将实参值传送给变参 在返回时将变参的值传给实参。 传地址:在内部将变参用一个地址替换,调用时, 先执行地址传送,将实参地址传送给变参,在执 行过程中,对变参的操作实际变成对实参的操作。 实参 变参 1 2 实参 变参 X 地址X

3)子程序调用的内部操作 。执行调用时,系统完成的操作 ó返回地址进栈,为子程序的局部变量开辟空间 6为子程序准备数据:计算实参值,并将其值送给 形参 6转入子程序入口地址 返回时,系统完成的操作: ó变参或函数的值保存到回传变量中 6从栈顶取返回地址 6返回调用程序 6将回传变量的值送给实参
7 ❖ 3)子程序调用的内部操作 ❖ 执行调用时,系统完成的操作 返回地址进栈,为子程序的局部变量开辟空间 为子程序准备数据:计算实参值,并将其值送给 形参 转入子程序入口地址 ❖ 返回时,系统完成的操作: 变参或函数的值保存到回传变量中 从栈顶取返回地址 返回调用程序 将回传变量的值送给实参
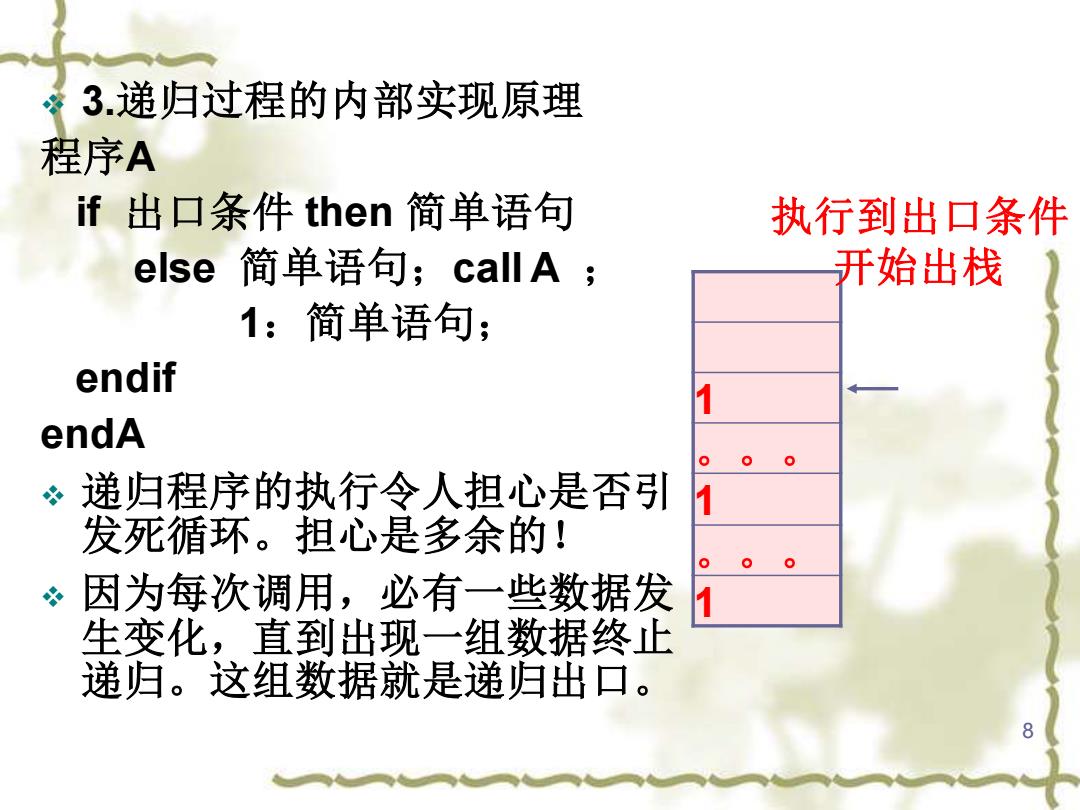
3.递归过程的内部实现原理 程序A if出口条件then简单语句 执行到出口条件 else简单语句;call A; 开始出栈 1:简单语句; endif endA 0 递归程序的执行令人担心是否引 发死循环。担心是多余的! 0 因为每次调用,必有一些数据发 生变化,直到出现一组数据终止 递归。这组数据就是递归出口
8 ❖ 3.递归过程的内部实现原理 程序A if 出口条件 then 简单语句 else 简单语句;call A ; 1:简单语句; endif endA ❖ 递归程序的执行令人担心是否引 发死循环。担心是多余的! ❖ 因为每次调用,必有一些数据发 生变化,直到出现一组数据终止 递归。这组数据就是递归出口。 1 。。。 1 。。。 1 执行到出口条件 开始出栈

递归举例 。间接递归 。直接递归 proc p1(n){ proc fact (n) if n>0 then if n=0 then return 1 if odd(n)then p1(n-1); else return n*fact(n-1) print n; else p2(n-1);print n; proc p2(n){ if n>0 then if n mod 3==0 then p1(n-1) else p2(n-1)
9 递归举例 ❖ 直接递归 proc fact(n) if n=0 then return 1 else return n*fact(n-1) ❖ 间接递归 proc p1(n){ if n>0 then if odd(n) then p1(n-1); print n; else p2(n-1);print n; } proc p2(n){ if n>0 then if n mod 3==0 then p1(n-1) else p2(n-1) }
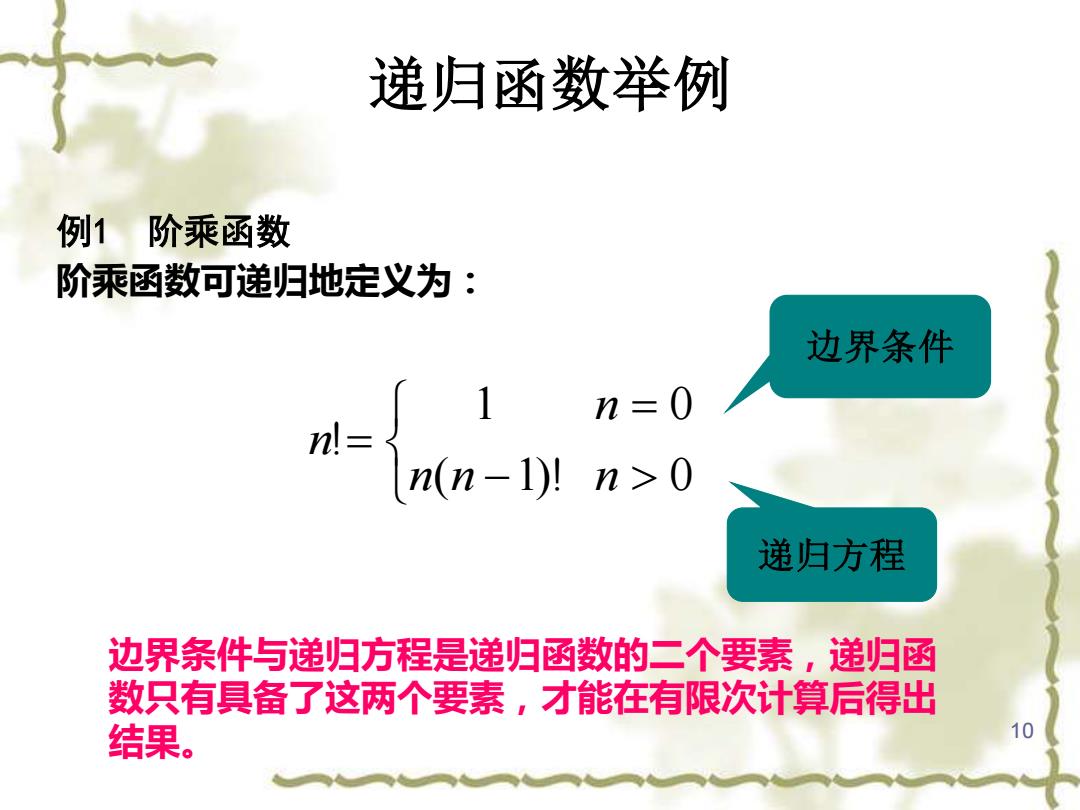
递归函数举例 例1阶乘函数 阶乘函数可递归地定义为: 边界条件 n= n(n-1)!n>0 递归方程 边界条件与递归方程是递归函数的二个要素,递归函 数只有具备了这两个要素,才能在有限次计算后得出 结果。 10
10 例1 阶乘函数 阶乘函数可递归地定义为: 0 0 ( 1)! 1 ! = − = n n n n n 边界条件 递归方程 边界条件与递归方程是递归函数的二个要素,递归函 数只有具备了这两个要素,才能在有限次计算后得出 结果。 递归函数举例