
Game theory in computer science Shengyu Zhang The Chinese University of Hong Kong
Shengyu Zhang The Chinese University of Hong Kong

Map Intro to strategic-form games aTwo forms Examples oNE and CE Algorithmic questions in games Hardness of finding an NE and CE Congestion games Game theory applied to computer science
Map ◼ Intro to strategic-form games ❑ Two forms ❑ Examples ❑ NE and CE ◼ Algorithmic questions in games ❑ Hardness of finding an NE and CE ❑ Congestion games ◼ Game theory applied to computer science

Part I.strategic-form games
Part I. strategic-form games

Game:Two basic forms SCISSORS strategic (normal)form extensive form
Game: Two basic forms strategic (normal) form extensive form

First example:Prisoner's dilemma Two prisoners are on trial for a crime,each can either confess or remain silent. Confess Silent If both silent:both serve 2 years. If only one confesses:he 4 5 serves 1 year and the other Confess 4 serves 5 years. If both confess:both serve 4 years. 2 What would you do if you Silent are Prisoner Blue?Red? 5 2
First example: Prisoner’s dilemma ◼ Two prisoners are on trial for a crime, each can either confess or remain silent. ◼ If both silent: both serve 2 years. ◼ If only one confesses: he serves 1 year and the other serves 5 years. ◼ If both confess: both serve 4 years. ◼ What would you do if you are Prisoner Blue? Red? Confess Silent Confess 4 4 5 1 Silent 1 5 2 2

Example 1:Prisoners'dilemma By a case-by-case analysis, we found that both Prisoners would confess, Confess Silent regardless of what the other chooses. Embarrassingly,they could have both chosen“Silent"”to 4 5 serve less years. Confess 4 1 But people are selfish:They only care about their own payoff. 1 Resulting a dilemma:You 2 Silent pay two more years for 5 2 being selfish
Example 1: Prisoners’ dilemma ◼ By a case-by-case analysis, we found that both Prisoners would confess, regardless of what the other chooses. ◼ Embarrassingly, they could have both chosen “Silent” to serve less years. ◼ But people are selfish: They only care about their own payoff. ◼ Resulting a dilemma: You pay two more years for being selfish. Confess Silent Confess 4 4 5 1 Silent 1 5 2 2
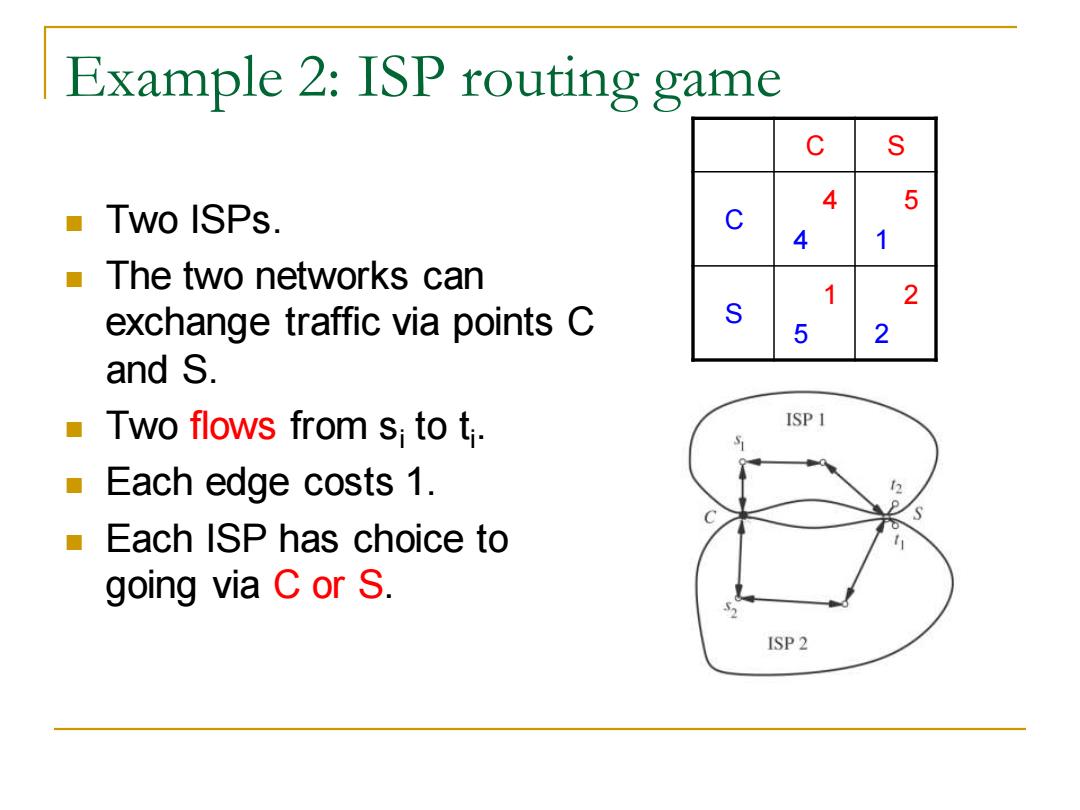
Example 2:ISP routing game C S 4 5 Two ISPs. C 4 1 a The two networks can 1 2 exchange traffic via points C S 5 2 and S. Two flows from s;to t. ISP 1 Each edge costs 1. 2 P Each ISP has choice to going via C or S. ISP 2
Example 2: ISP routing game ◼ Two ISPs. ◼ The two networks can exchange traffic via points C and S. ◼ Two flows from si to ti . ◼ Each edge costs 1. ◼ Each ISP has choice to going via C or S. C S C 4 4 5 1 S 1 5 2 2

Example 3:Pollution game N countries Each country faces the choice of either controlling pollution or not. Pollution control costs 3 for each country. Each country that pollutes adds 1 to the cost of all countries. What would you do if you are one of those countries? Suppose k countries don't control. For them:cost k For others:cost 3+k So all countries don't control!
Example 3: Pollution game ◼ N countries ◼ Each country faces the choice of either controlling pollution or not. ❑ Pollution control costs 3 for each country. ◼ Each country that pollutes adds 1 to the cost of all countries. ◼ What would you do if you are one of those countries? ◼ Suppose k countries don’t control. ❑ For them: cost = k ❑ For others: cost = 3+k ◼ So all countries don’t control!

Example 4:Battle of the sexes A boy and a girl want to decide whether to go to watch a baseball or a B S softball game. The boy prefers baseball 6 1 and the girl prefers softball. B 5 1 But they both like to spend the time together rather 2 5 than separately. S 2 6 What would you do?
Example 4: Battle of the sexes ◼ A boy and a girl want to decide whether to go to watch a baseball or a softball game. ◼ The boy prefers baseball and the girl prefers softball. ◼ But they both like to spend the time together rather than separately. ◼ What would you do? B S B 6 5 1 1 S 2 2 5 6

Formal definition In all previous games: There are a number of players Each has a set of strategies to choose from Each aims to maximize his/her payoff,or minimize his/her loss. Formally, ▣n-players. Each player i has a set Si of strategies. 0 LetS=Six…×Sn-A joint strategy is an s=s.sn- Each player i has a payoff function u(s)depending on a joint strategy s
Formal definition ◼ In all previous games: ❑ There are a number of players ❑ Each has a set of strategies to choose from ❑ Each aims to maximize his/her payoff, or minimize his/her loss. ◼ Formally, ❑ n-players. ❑ Each player i has a set Si of strategies. ❑ Let S = S1 ⋯ Sn . A joint strategy is an s = s1…sn . ❑ Each player i has a payoff function ui (s) depending on a joint strategy s