
CSCI 3160 Design and Analysis of Algorithms Tutorial 9 Chengyu Lin
CSCI 3160 Design and Analysis of Algorithms Tutorial 9 Chengyu Lin

Outline ·Stable Matching ·Secretary Problem
Outline • Stable Matching • Secretary Problem

Stable Matching 免 免免 Figures borrowed from Lecture Notes of CSCI2110
Stable Matching Figures borrowed from Lecture Notes of CSCI2110
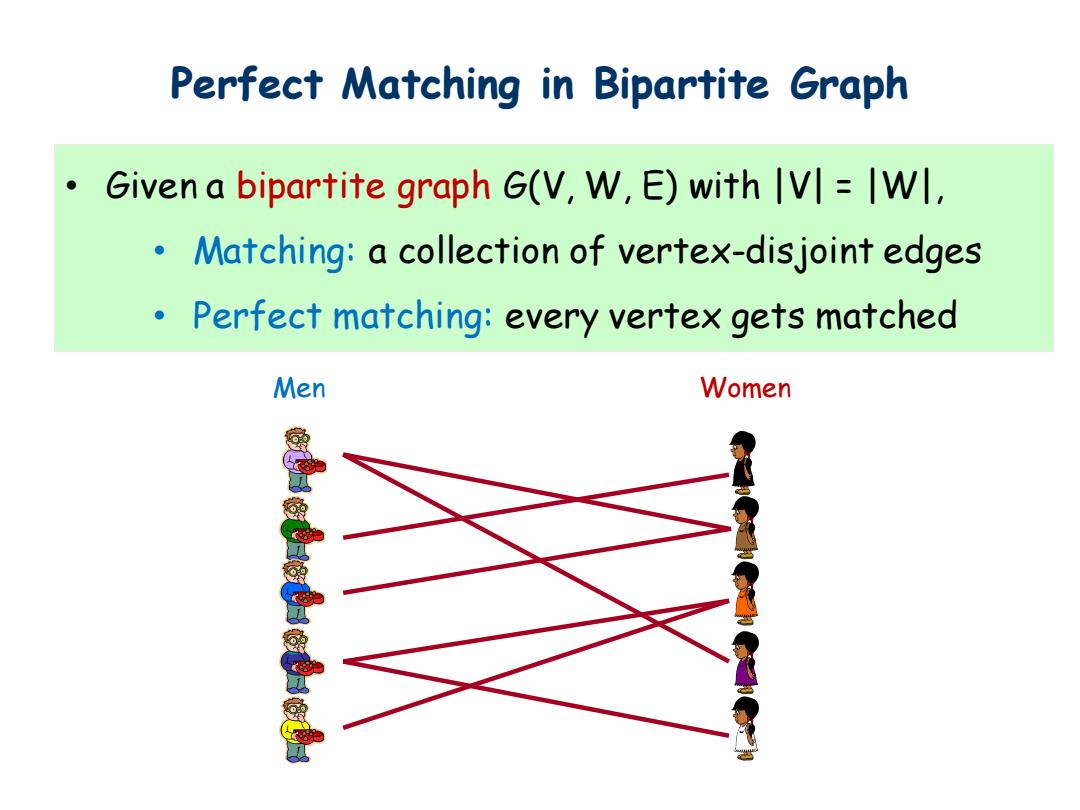
Perfect Matching in Bipartite Graph Given a bipartite graph G(V,W,E)with IVI Wl, 。. Matching:a collection of vertex-disjoint edges Perfect matching:every vertex gets matched Men Women
Perfect Matching in Bipartite Graph • Given a bipartite graph G(V, W, E) with |V| = |W|, • Matching: a collection of vertex-disjoint edges • Perfect matching: every vertex gets matched Men Women

Preference Each man has a preference list of all women Each woman has a preference list of all men Assume there is no tie Men Women 1:CBEAD A:35214 2:ABECD B:52143 3:DCBAE C:43512 4:ACDBE D:12345 5:ABDEC E:23415
Preference Men Women 1: CBEAD A : 35214 2 : ABECD B : 52143 3 : DCBAE C : 43512 4 : ACDBE D : 12345 5 : ABDEC E : 23415 • Each man has a preference list of all women • Each woman has a preference list of all men • Assume there is no tie

Blocking Pairs A Blocking Pair is a pair of man and woman that prefer each other to their current partners. Man 4 prefer Woman C to current partner Woman B Woman C prefer Man 4 to current partner Man 1 Men Women 1:CBEAD A:35214 2:ABECD B:52143 3:DCBAE C:43512 4:ACDBE D:12345 5:ABDEC E:23415
Blocking Pairs A Blocking Pair is a pair of man and woman that prefer each other to their current partners. Men Women 1: CBEAD A : 35214 2 : ABECD B : 52143 3 : DCBAE C : 43512 4 : ACDBE D : 12345 5 : ABDEC E : 23415 • Man 4 prefer Woman C to current partner Woman B • Woman C prefer Man 4 to current partner Man 1
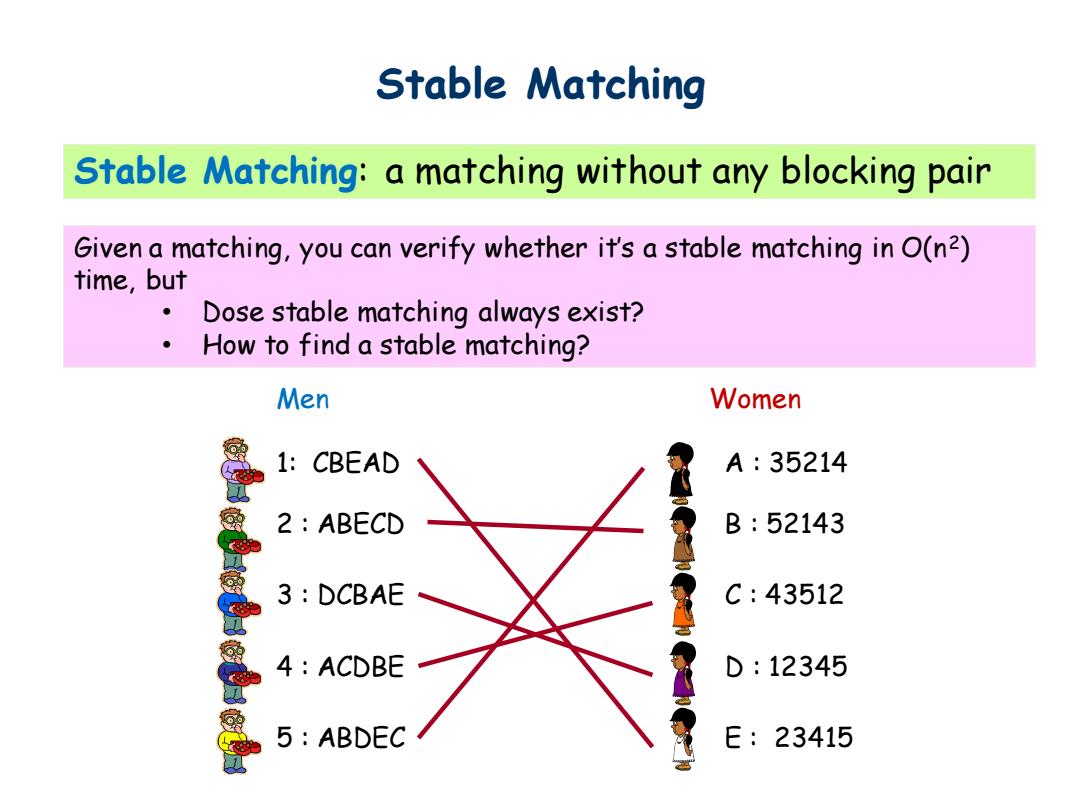
Stable Matching Stable Matching:a matching without any blocking pair Given a matching,you can verify whether it's a stable matching in O(n2) time,but Dose stable matching always exist? 。 How to find a stable matching? Men Women 1: CBEAD A:35214 2:ABECD B:52143 3:DCBAE C:43512 4:ACDBE D:12345 5:ABDEC E:23415
Stable Matching Men Women 1: CBEAD A : 35214 2 : ABECD B : 52143 3 : DCBAE C : 43512 4 : ACDBE D : 12345 5 : ABDEC E : 23415 Stable Matching: a matching without any blocking pair Given a matching, you can verify whether it’s a stable matching in O(n2) time, but • Dose stable matching always exist? • How to find a stable matching?
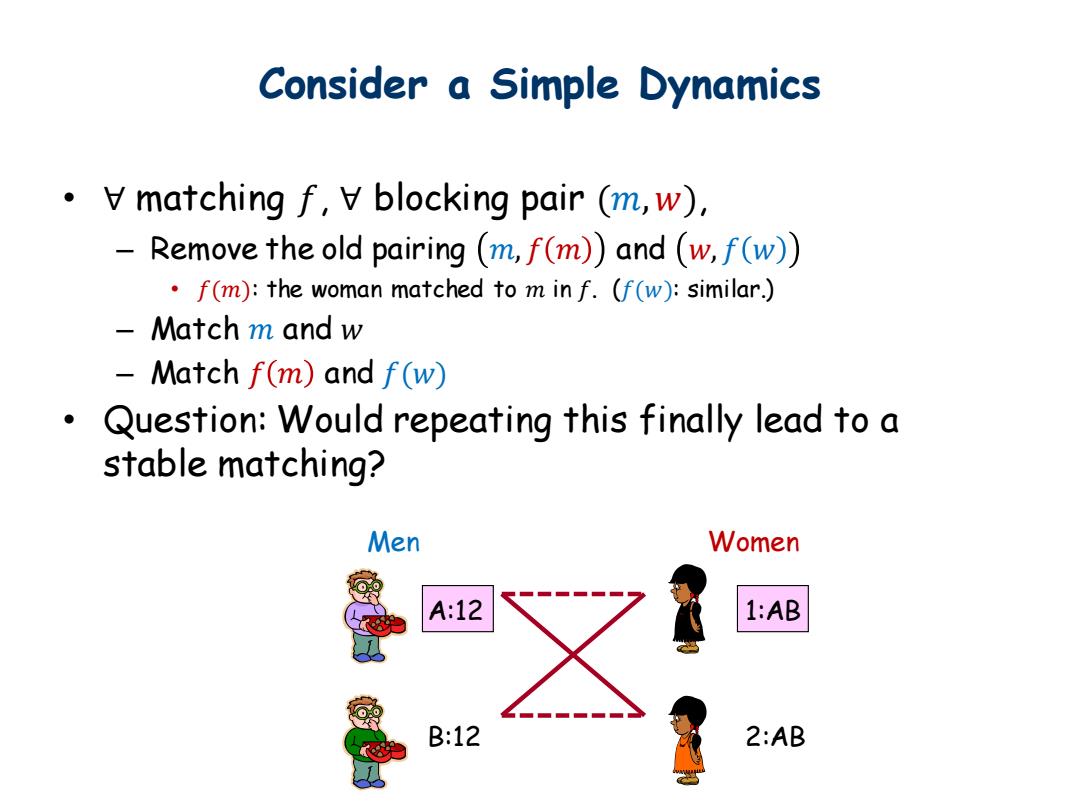
Consider a Simple Dynamics ·廿matching f,V blocking pair(m,w), -Remove the old pairing (m,f(m))and (w,f(w)) f(m):the woman matched to m in f.(f(w):similar.) Match m and w Match f(m)and f(w) Question:Would repeating this finally lead to a stable matching? Men Women A:12 1:AB B:12 2:AB
Consider a Simple Dynamics • ∀ matching 𝑓, ∀ blocking pair (𝑚,𝑤), – Remove the old pairing 𝑚, 𝑓 𝑚 and 𝑤, 𝑓 𝑤 • 𝑓(𝑚): the woman matched to 𝑚 in 𝑓. (𝑓(𝑤): similar.) – Match 𝑚 and 𝑤 – Match 𝑓 𝑚 and 𝑓(𝑤) • Question: Would repeating this finally lead to a stable matching? Men A:12 B:12 1:AB 2:AB Women

Counterexample with 2 Men and 2 Women? Men Women 2 Man A and Woman 1 have no incentive to breakup Counterexample with 2 Men and 2 Women is IMPOSSIBLE
Counterexample with 2 Men and 2 Women? Men Women A B 1 2 Man A and Woman 1 have no incentive to breakup Counterexample with 2 Men and 2 Women is IMPOSSIBLE !

Counterexample with 3 Men and 3 Women? Men Women A:?22 1:?2? B:?? 2:222 C:?22 3:2?2
Counterexample with 3 Men and 3 Women? Men Women A:??? B:??? C:??? 1:??? 2:??? 3:???