
CSC3160: Design and Analysis of Algorithms Week 5: Dynamic Programming Instructor: Shengyu Zhang 1
Instructor: Shengyu Zhang 1

About midterm Time:Mar 3,2:50pm -4:50pm. Place:This lecture room. Open book,open lecture notes. But no Internet allowed. Scope:First 6 lectures 2
About midterm ◼ Time: Mar 3, 2:50pm – 4:50pm. ◼ Place: This lecture room. ◼ Open book, open lecture notes. ❑ But no Internet allowed. ◼ Scope: First 6 lectures 2

Dynamic Programming A simple but non-trivial method for designing algorithms Achieve much better efficiency than naive ones. A couple of examples will be exhibited and analyzed. 3
Dynamic Programming ◼ A simple but non-trivial method for designing algorithms ◼ Achieve much better efficiency than naïve ones. ◼ A couple of examples will be exhibited and analyzed. 3

Problem 1:Chain matrix multiplication 4
Problem 1: Chain matrix multiplication 4

Suppose we want to multiply four matrices We want to multiply four matrices:A×B×C×D. Dimensions:A5ox20,B20x1,C1x10,D10x100 ■ Assume:cost (Xmxn X Ynxi)=mnl. The order matters! ▣A×(B×C)×D):20×1×10+20×10×100+50×20×100 120,200 A×(B×(C×D):1×10×100+20×1×100+50×20×100= 103,000 口(A×B)×(C×D):50×20×1+1×10×100+50×1×100=7,000 口(A×B)×C)×D:50×20×1+50×1×10+50×10×100=51,500 0 (A×(B×C)×D:20×1×10+50×20×10+50×10×100=60,200 Question:In what order should we multiply them? 5
Suppose we want to multiply four matrices ◼ We want to multiply four matrices: 𝐴 × 𝐵 × 𝐶 × 𝐷. ◼ Dimensions: 𝐴50×20, 𝐵20×1 , 𝐶1×10, 𝐷10×100 ◼ Assume: cost (𝑋𝑚×𝑛 × 𝑌𝑛×𝑙 ) = 𝑚𝑛𝑙. ❑ 𝐴 × 𝐵 × 𝐶 × 𝐷 : 20 × 1 × 10 + 20 × 10 × 100 + 50 × 20 × 100 = 120,200 ❑ 𝐴 × 𝐵 × 𝐶 × 𝐷 : 1 × 10 × 100 + 20 × 1 × 100 + 50 × 20 × 100 = 103,000 ❑ 𝐴 × 𝐵 × 𝐶 × 𝐷 : 50 × 20 × 1 + 1 × 10 × 100 + 50 × 1 × 100 = 7,000 ❑ 𝐴 × 𝐵 × 𝐶 × 𝐷: 50 × 20 × 1 + 50 × 1 × 10 + 50 × 10 × 100 = 51,500 ❑ 𝐴 × 𝐵 × 𝐶 × 𝐷: 20 × 1 × 10 + 50 × 20 × 10 + 50 × 10 × 100 = 60,200 ◼ Question: In what order should we multiply them? The order matters! 5

Key property General question:We have matrices A1,...An,we want to find the best order for A1×…×An o Dimension of Ai:mi-1x mi ■ One way to find the optimum:Consider the last step. Suppose:(A1×…×Ai)×(Ai+1×…×An)for s0mei∈{1,.,n-1}. cost(1,n)=cost(1,i)+cost(i+1,n)+ momimn 6
Key property ◼ General question: We have matrices 𝐴1, …, 𝐴𝑛, we want to find the best order for 𝐴1 × ⋯ × 𝐴𝑛 ❑ Dimension of 𝐴𝑖 : 𝑚𝑖−1 × 𝑚𝑖 ◼ One way to find the optimum: Consider the last step. ❑ Suppose: 𝐴1 × ⋯ × 𝐴𝑖 × 𝐴𝑖+1 × ⋯ × 𝐴𝑛 for some 𝑖 ∈ 1,… , 𝑛 − 1 . ◼ cost 1, 𝑛 = cost 1, 𝑖 + cost 𝑖 + 1, 𝑛 + 𝑚0𝑚𝑖𝑚𝑛 6

Algorithm But what is a best i? We don't know...Try all and take the min. bestcost(1,n) min bestcost(1,i)+bestcost(i+1,n)+momimn bestcost(i,j):the min cost of computing(A;×…×A;) ■ How to solve(A1×…XAi)and(Ai+1×…×An)? Attempt:Same way,i.e.a recursion Complexity: ▣T(1,n)=∑(T(1,i)+T(i+1,n)+0(1) Exponential!
Algorithm ◼ But what is a best 𝑖? ◼ We don’t know… Try all and take the min. bestcost(1,𝑛) = min 𝑖 bestcost(1,𝑖) + bestcost(𝑖 + 1, 𝑛) + 𝑚0𝑚𝑖𝑚𝑛 ❑ bestcost(𝑖,𝑗): the min cost of computing 𝐴𝑖 × ⋯ × 𝐴𝑗 ◼ How to solve 𝐴1 × ⋯ × 𝐴𝑖 and 𝐴𝑖+1 × ⋯ × 𝐴𝑛 ? ◼ Attempt: Same way, i.e. a recursion ◼ Complexity: ❑ 𝑇(1, 𝑛) = σ𝑖 (𝑇(1, 𝑖) + 𝑇(𝑖 + 1, 𝑛) + 𝑂(1)) ❑ Exponential! 7
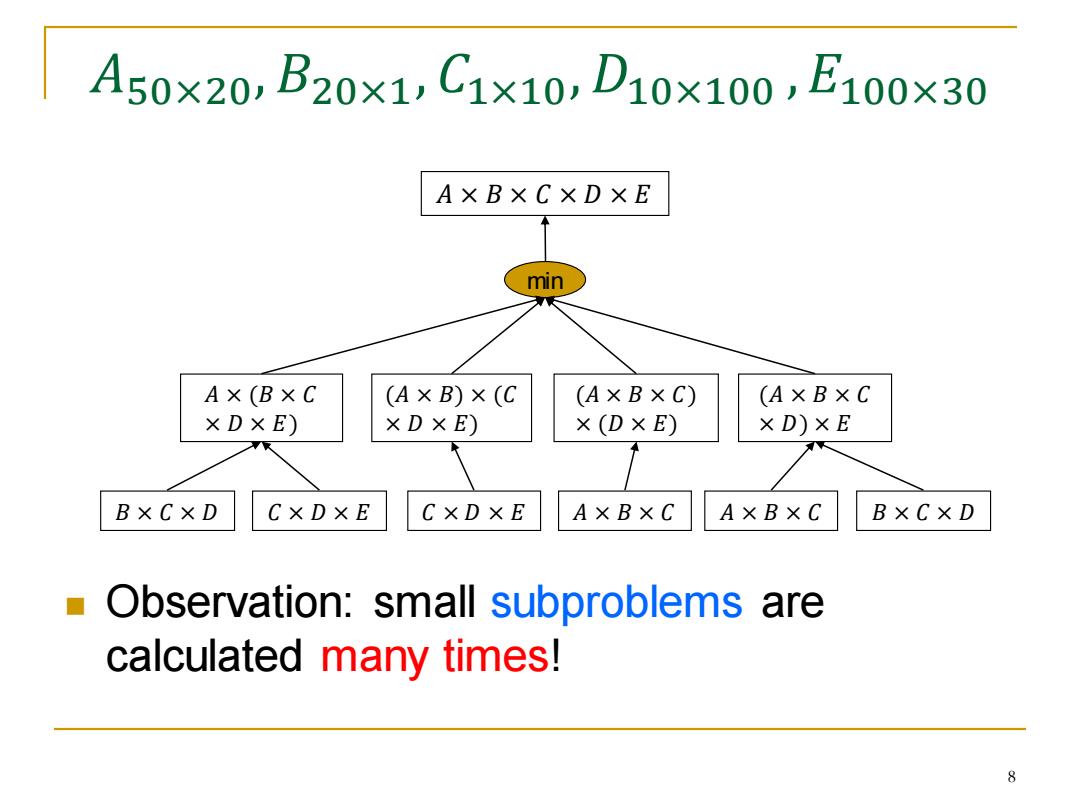
A50×20,B20X1,C1x10,D10×100,E100×30 AXBXC×DXE min A×(BXC (AXB)×(C (A×B×C) (A×B×C x D X E) XD X E) ×(DXE) XD)XE BXCXD CXDXE CXD XE AXBXC AXBXC B X C X D Observation:small subproblems are calculated many times! 8
𝐴50×20, 𝐵20×1, 𝐶1×10,𝐷10×100 ,𝐸100×30 ◼ Observation: small subproblems are calculated many times! 𝐴 × (𝐵 × 𝐶 × 𝐷 × 𝐸) 𝐴 × 𝐵 × 𝐶 × 𝐷 × 𝐸 (𝐴 × 𝐵) × (𝐶 × 𝐷 × 𝐸) (𝐴 × 𝐵 × 𝐶) × (𝐷 × 𝐸) min 𝐵 × 𝐶 × 𝐷 𝐶 × 𝐷 × 𝐸 𝐶 × 𝐷 × 𝐸 𝐴 × 𝐵 × 𝐶 𝐴 × 𝐵 × 𝐶 𝐵 × 𝐶 × 𝐷 (𝐴 × 𝐵 × 𝐶 × 𝐷) × 𝐸 8

What did we observe? Why not just do it once and store the result for later reference? When needed later:simply look up the stored result. That's dynamic programming. First compute the small problems and store the answers Then compute the large problems using the stored results of smaller subproblems
What did we observe? ◼ Why not just do it once and store the result for later reference? ❑ When needed later: simply look up the stored result. ◼ That’s dynamic programming. ❑ First compute the small problems and store the answers ❑ Then compute the large problems using the stored results of smaller subproblems. 9
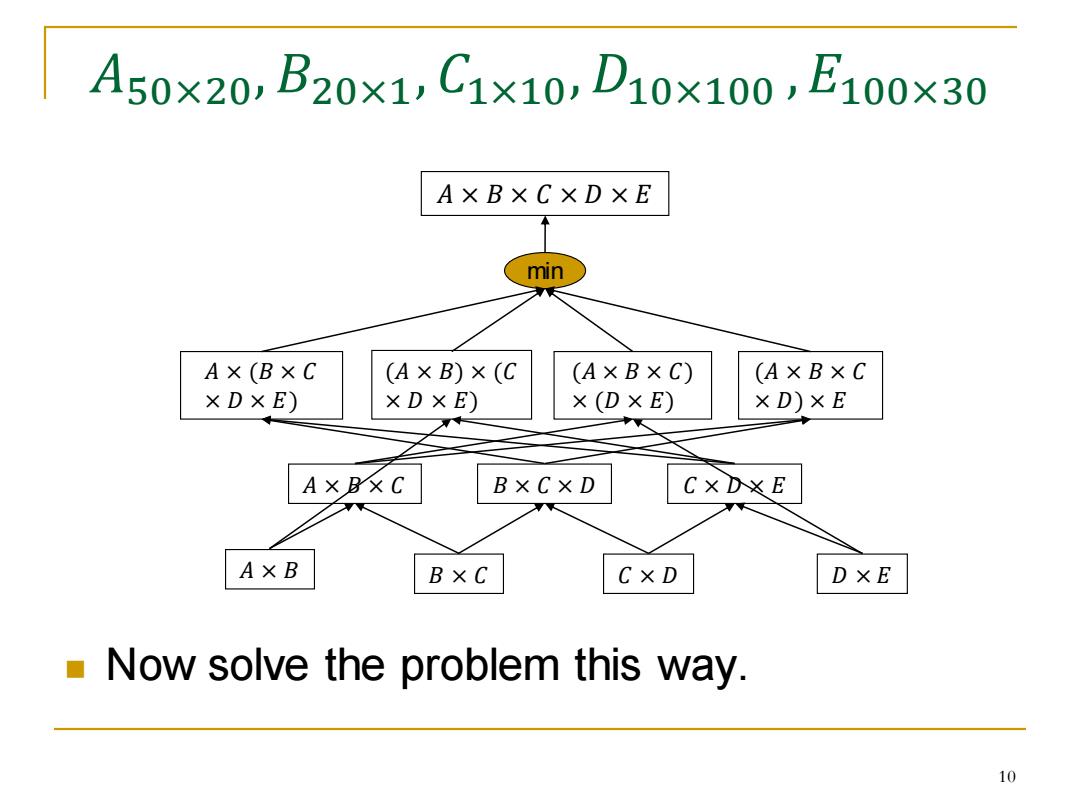
A50×20,B20×1,C1x10,D10×100,E100x30 AXBX C X D XE min A×(BXC (AXB)×(C (A×B×C) (AxBxC XDXE) X D X E) x (D X E) XD)XE AXBXC BXCXD CXDXE AXB BxC CXD DXE Now solve the problem this way. 10
𝐴50×20, 𝐵20×1, 𝐶1×10,𝐷10×100 ,𝐸100×30 𝐴 × (𝐵 × 𝐶 × 𝐷 × 𝐸) 𝐴 × 𝐵 × 𝐶 × 𝐷 × 𝐸 (𝐴 × 𝐵) × (𝐶 × 𝐷 × 𝐸) (𝐴 × 𝐵 × 𝐶) × (𝐷 × 𝐸) min 𝐴 × 𝐵 × 𝐶 𝐵 × 𝐶 × 𝐷 𝐶 × 𝐷 × 𝐸 (𝐴 × 𝐵 × 𝐶 × 𝐷) × 𝐸 𝐴 × 𝐵 𝐵 × 𝐶 𝐶 × 𝐷 𝐷 × 𝐸 ◼ Now solve the problem this way. 10