
cMSc5706TopicsinTheoreticalcoMputerScience wek1法Qat如me0mpig Instructor:Shengyu Zhang 1
Instructor: Shengyu Zhang 1

Roadmap Intro to math model of quantum mechanics Review of quantum algorithms The power of quantum computers. 。Quantum games
Roadmap • Intro to math model of quantum mechanics • Review of quantum algorithms • The power of quantum computers. • Quantum games

Postulate 1:States State space:Every isolated physical system corresponds to a unit vector in a complex vector space. -Unit vector:2-norm is 1. Such states are called pure states. ·Ve use a weird“ket"notation'〉to denote such a state
Postulate 1: States • State space: Every isolated physical system corresponds to a unit vector in a complex vector space. – Unit vector: ℓ2 -norm is 1. • Such states are called pure states. • We use a weird “ket” notation ⋅ to denote such a state

Ket notation ·Mathematically,〉is a column vector. ·And(is a row vector. ·yΦ)is the inner product between the vectorsΦ)andlψ). ·〈ylMlψ〉is just the quadratic formψrMp
Ket notation • Mathematically, ⋅ is a column vector. • And ⋅ is a row vector. • 𝜓 𝜙 is the inner product between the vectors 𝜙 and 𝜓 . • 𝜓 𝑀 𝜓 is just the quadratic form 𝜓 𝑇𝑀𝜓
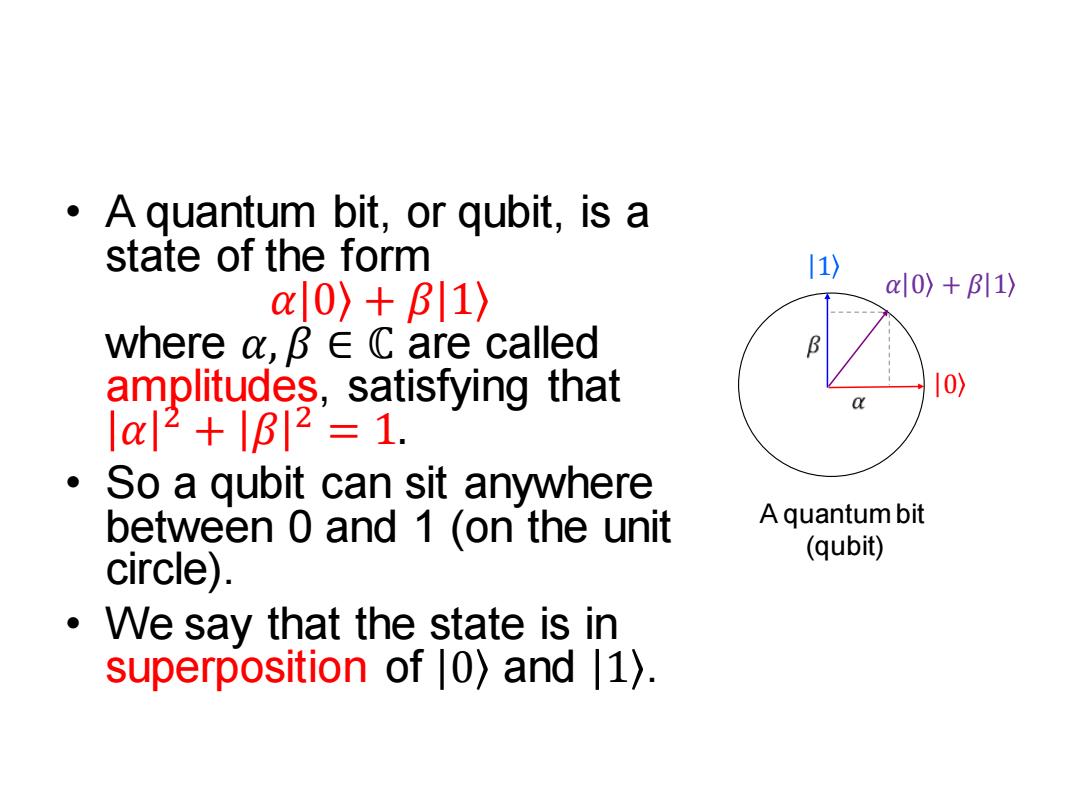
A quantum bit,or qubit,is a state of the form 11) 0〉+B11〉 a0)+B11)》 where a,B∈C are called amplitudes,satisfying that 10)》 |2+lB12=1. 。 So a qubit can sit anywhere between 0 and 1 (on the unit A quantum bit (qubit) circle). We say that the state is in superposition of |0)and 1)
• A quantum bit, or qubit, is a state of the form 𝛼 0 + 𝛽 1 where 𝛼, 𝛽 ∈ ℂ are called amplitudes, satisfying that 𝛼 2 + 𝛽 2 = 1. • So a qubit can sit anywhere between 0 and 1 (on the unit circle). • We say that the state is in superposition of 0 and 1 . A quantum bit (qubit) 𝛼 0 + 𝛽 1 0 1

Postulate 2:operation Evolution:The evolution ofa closed quantum system is described by a unitary transformation. ·That is,if a system is in stateψ〉at time t, and in stateψ2〉at time t2,then there is a unitary transformation U s.t. |2〉=U小ψ1〉. Unitary transformation:U =U-1 -Recall:UT =(U)*,transpose complex conjugate -You can think of it as a rotation operation
Postulate 2: operation • Evolution: The evolution of a closed quantum system is described by a unitary transformation. • That is, if a system is in state 𝜓1 at time 𝑡1, and in state 𝜓2 at time 𝑡2, then there is a unitary transformation 𝑈 s.t. 𝜓2 = 𝑈 𝜓1 . • Unitary transformation: 𝑈 † = 𝑈 −1 – Recall: 𝑈 † = 𝑈 𝑇 ∗ , transpose + complex conjugate – You can think of it as a rotation operation

Postulate 3:measurement Measurement:We can only observe a quantum system by measuring it. The outcome of the measurement is random. And the system is changed by the measurement
Postulate 3: measurement • Measurement: We can only observe a quantum system by measuring it. • The outcome of the measurement is random. • And the system is changed by the measurement

·If we measure qubit a0〉+βl1) in the computational basis 11) 10),|1),then outcome "o" al0)+B11) occurs with prob.|a|2,and outcome“1”occurs with prob. 10) IB12. ·The system becomes |0〉if outcome“o”occurs,and A quantum bit becomes|1〉if outcome“1” (qubit) occurs. The system collapses
• If we measure qubit 𝛼 0 + 𝛽 1 in the computational basis 0 , 1 , then outcome “0” occurs with prob. 𝛼 2 , and outcome “1” occurs with prob. 𝛽 2 . • The system becomes 0 if outcome “0” occurs, and becomes 1 if outcome “1” occurs. – The system collapses. A quantum bit (qubit) 𝛼 0 + 𝛽 1 0 1

Measurement on general states In general,an orthogonal measurement of a d-dim state is given by an orthonormal basis{lψ1),.lyd}. ·If we measure stateΦ)in basis ly),.lψd},then outcome i∈{1,.,d occurs with prob.lKφlψ;l2. ·The system collapses toψ;〉if outcome i occurs
Measurement on general states • In general, an orthogonal measurement of a 𝑑-dim state is given by an orthonormal basis 𝜓1 ,… 𝜓𝑑 . • If we measure state 𝜙 in basis 𝜓1 ,… 𝜓𝑑 , then outcome 𝑖 ∈ 1,… , 𝑑 occurs with prob. 𝜙|𝜓𝑖 2 . • The system collapses to 𝜓𝑖 if outcome 𝑖 occurs

Postulate 4:composition Composition:The state of the joint system (Si,S2),where S1 is in stateψ〉andS2in lp2),islψ1〉☒lψ2). ☒:tensor product of vectors. -(a1,a2)☒(b1,b2,b3)=(a1b1,a1b2,a1b3,a2b1,a2b2,a2b3). -dim(lw1〉⑧lψ2)=dim(ψ1)·dim(lψ2) - size(lψ1〉⑧l2)=size(lψ1)+size(lψ2) size:number of qubits. 、Notation:l0)8n=l0〉☒…☒l0),n times
Postulate 4: composition • Composition: The state of the joint system (𝑆1, 𝑆2), where 𝑆1 is in state 𝜓1 and 𝑆2 in 𝜓2 , is 𝜓1 ⊗ 𝜓2 . • ⊗: tensor product of vectors. – 𝑎1, 𝑎2 ⊗ 𝑏1, 𝑏2, 𝑏3 = (𝑎1𝑏1, 𝑎1𝑏2, 𝑎1𝑏3, 𝑎2𝑏1, 𝑎2𝑏2, 𝑎2𝑏3). – dim 𝜓1 ⊗ 𝜓2 = dim 𝜓1 ⋅ dim 𝜓2 – size 𝜓1 ⊗ 𝜓2 = size 𝜓1 + size 𝜓2 • size: number of qubits. • Notation: 0 ⊗𝑛 = 0 ⊗ ⋯ ⊗ 0 , 𝑛 times