
Tutorial 8:Further Topics on Random Variables 1 Weiwen LIU wwliu@cuhk.edu.hk March 20,2017 1
Tutorial 8: Further Topics on Random Variables 1 Weiwen LIU wwliu@cuhk.edu.hk March 20, 2017 1

Derived distributions Given Y=g(X)of a continuous random variable X and PDF of X, how to calculate the PDF of y? ·Two step approach
Derived distributions • Given 𝑌 = 𝑔(𝑋) of a continuous random variable 𝑋 and PDF of 𝑋, how to calculate the PDF of 𝑌? • Two step approach 2

Calculation of PDF of Y =g( 1.Calculate the CDF Fy of Y using the formula Fy)=P(g(X)≤y)=f (x)dx J{xlg(x)≤y3 2.Differentiate Fy to obtain the PDF fy of Y: dFy fy(y)=dy (y) 3
Calculation of PDF of 𝑌 = 𝑔(𝑋) 1. Calculate the CDF 𝐹𝑌 of 𝑌 using the formula 𝐹𝑌 𝑦 = 𝑃 𝑔 𝑋 ≤ 𝑦 = න {𝑥|𝑔(𝑥)≤𝑦} 𝑓𝑋(𝑥)𝑑𝑥 2. Differentiate 𝐹𝑌 to obtain the PDF 𝑓𝑌 of 𝑌: 𝑓𝑌 𝑦 = 𝑑𝐹𝑌 𝑑𝑦 𝑦 . 3

Calculation of PDF of Y =g() ·Linear case: The PDF of y ax +b in terms of the PDFX. 0)-0=6(。 dF 。Monotonic Case: Suppose that g is monotonic and that for some function h and all x in the range of X we have y=g(x)if and only ifx=h(y). Assume that h is differentiable. 0)=a0o)
Calculation of PDF of 𝑌 = 𝑔(𝑋) • Linear case: • The PDF of 𝑌 = 𝑎𝑋 + 𝑏 in terms of the PDF 𝑋. 𝑓𝑌 𝑦 = 𝑑𝐹𝑌 𝑑𝑦 𝑦 = 1 |𝑎| 𝑓𝑋 𝑦 − 𝑏 𝑎 • Monotonic Case: • Suppose that 𝑔 is monotonic and that for some function ℎ and all 𝑥 in the range of 𝑋 we have 𝑦 = 𝑔 𝑥 if and only if 𝑥 = ℎ(𝑦). • Assume that ℎ is differentiable. 𝑓𝑌 𝑦 = 𝑓𝑋 ℎ(𝑦) 𝑑ℎ 𝑑𝑦 (𝑦) 4

Example 1 Let X be a random variable with PDF fx.Find the PDF of the random variable y =X, ·(a)whenfx(x)= ,f-2<x≤1, 0,otherwise; (whenf(&=ze-2,ifx之0” otherwise; .(c)for general fx(x). 5
Example 1 • Let X be a random variable with PDF 𝑓𝑋. Find the PDF of the random variable 𝑌 = |𝑋|, • (a) when 𝑓𝑋 𝑥 = ቐ 1 3 , 𝑖𝑓 − 2 0, 0, 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒; • (c) for general 𝑓𝑋(𝑥). 5

Example 1 斥m=m+R(- Since Y =X,you can visualize the PDF for any given y as ify≥0 0, ify<0 ·Also note that since Y=lXl,Y≥0. 6
Example 1 • Since 𝑌 = 𝑋 , you can visualize the PDF for any given 𝑦 as 𝑓𝑌(𝑦) = ቊ 𝑓𝑋 𝑦 + 𝑓𝑋 −𝑦 , 𝑖𝑓 𝑦 ≥ 0 0, 𝑖𝑓 𝑦 < 0 • Also note that since 𝑌 = |𝑋|, 𝑌 ≥ 0. 6
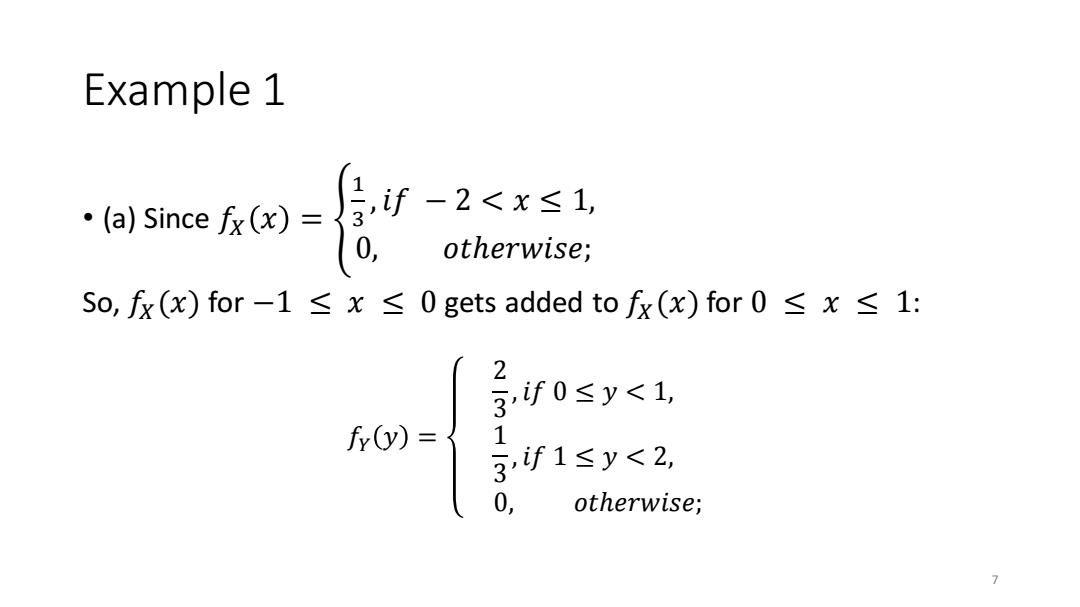
Example 1 ·(a)Sincefx(x)= f-2<x≤1 0, otherwise; So,fx(x)for-1≤x≤0 gets added tofx(x)for0≤x≤1: 0≤ys, f(y)={ 3,f1≤y<2, 0, otherwise; 7
Example 1 • (a) Since 𝑓𝑋 𝑥 = ቐ 1 3 , 𝑖𝑓 − 2 < 𝑥 ≤ 1, 0, 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒; So, 𝑓𝑋(𝑥) for −1 ≤ 𝑥 ≤ 0 gets added to 𝑓𝑋(𝑥) for 0 ≤ 𝑥 ≤ 1: 𝑓𝑌 𝑦 = 2 3 , 𝑖𝑓 0 ≤ 𝑦 < 1, 1 3 , 𝑖𝑓 1 ≤ 𝑦 < 2, 0, 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒; 7

Example 1 .(b)Here we are told X>0.So there are no negative values of X that need to be considered.Thus fy(y)=fx(x)= (2e-2x,if x>0, 10,otherwise. .(c)As explained in the beginning, f(y)=fx(y)+fx(-y). 8
Example 1 • (b) Here we are told 𝑋 > 0. So there are no negative values of 𝑋 that need to be considered. Thus f𝑌 y = 𝑓𝑋 𝑥 = ቊ 2𝑒 −2𝑥 ,𝑖𝑓 𝑥 > 0, 0, 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒. • (c) As explained in the beginning, 𝑓𝑌(𝑦) = 𝑓𝑋(𝑦) + 𝑓𝑋(−𝑦). 8

Example 2:archer shooting Two archers shoot at a target. The distance of each shot from the center of the target is uniformly distributed from 0 to 1,independent of the other shot. Question:What is the PDF of the distance of the winning shot from the center? 9
Example 2: archer shooting • Two archers shoot at a target. • The distance of each shot from the center of the target is uniformly distributed from 0 to 1, independent of the other shot. • Question: What is the PDF of the distance of the winning shot from the center? 9

Example 2:archer shooting Let X and Y be the distances from the center of the first and second shots,respectively. Z:the distance of the winning shot: Z=min,Y). Since X and Y are uniformly distributed over 0,1, 。we have,for all z∈[0,1], P(X≥z)=P(Y≥z)=1-z. 10
Example 2: archer shooting • Let 𝑋 and 𝑌 be the distances from the center of the first and second shots, respectively. • 𝑍: the distance of the winning shot: 𝑍 = min 𝑋, 𝑌 . • Since 𝑋 and 𝑌 are uniformly distributed over 0,1 , • we have, for all 𝑧 ∈ 0, 1 , 𝑃 𝑋 ≥ 𝑧 = 𝑃 𝑌 ≥ 𝑧 = 1 − 𝑧. 10