
Tutorial 10:Limit Theorems Weiwen LIU wwliu@cse.cuhk.edu.hk April 3,2017 1
Tutorial 10: Limit Theorems Weiwen LIU wwliu@cse.cuhk.edu.hk April 3, 2017 1

Markov and Chebyshev Inequalities These inequalities use the mean and possibly the variance of a random variable to draw conclusions on the probabilities of certain events. primarily useful in situations exact values or bounds for the mean and variance of a random variable X are easily computable. but the distribution of X is either unavailable or hard to calculate. 2
Markov and Chebyshev Inequalities • These inequalities use the mean and possibly the variance of a random variable to draw conclusions on the probabilities of certain events. • primarily useful in situations • exact values or bounds for the mean and variance of a random variable 𝑋 are easily computable. • but the distribution of 𝑋 is either unavailable or hard to calculate. 2

Markov inequality If a random variable X can only take nonnegative values,then pX之)≤W,for all>0 Loosely speaking,it asserts that if a nonnegative random variable has a small mean,then the probability that it takes a large value must also be small. 3
Markov inequality • If a random variable 𝑋 can only take nonnegative values, then 𝑃 𝑋 ≥ 𝑎 ≤ 𝐸 𝑋 𝑎 , for all 𝑎 > 0 Loosely speaking, it asserts that • if a nonnegative random variable has a small mean, then the probability that it takes a large value must also be small. 3

Example 1 Let X be uniformly distributed in the interval0,4 and note that E[X]=2. Then,the Markov inequality asserts that 2 P(X之2)≤2=1 2 P(X≥3)≤5=0.67. PX≥4)≤4=0.5 4
Example 1 • Let 𝑋 be uniformly distributed in the interval [0,4] and note that 𝐸[𝑋] = 2. • Then, the Markov inequality asserts that 𝑃 𝑋 ≥ 2 ≤ 2 2 = 1. 𝑃 𝑋 ≥ 3 ≤ 2 3 = 0.67. 𝑃 𝑋 ≥ 4 ≤ 2 4 = 0.5. 4

Example 1 By comparing with the exact probabilities P(X≥2)=0.5. P(X≥3)=0.25. P(X≥4)=0. We see that the bounds provided by the Markov inequality can be quite loose
Example 1 • By comparing with the exact probabilities 𝑃 𝑋 ≥ 2 = 0.5. 𝑃 𝑋 ≥ 3 = 0.25. 𝑃 𝑋 ≥ 4 = 0. • We see that the bounds provided by the Markov inequality can be quite loose. 5

Chebyshev inequality If X is a random variable with mean u and variance o2,then 02 P(IX-川≥c)≤c2, for all c >0 6
Chebyshev inequality • If 𝑋 is a random variable with mean 𝜇 and variance 𝜎 2 , then 𝑃 𝑋 − 𝜇 ≥ 𝑐 ≤ 𝜎 2 𝑐 2 , for all 𝑐 > 0 6

Example 2:Uninformative case Let X be uniformly distributed in 0,4. Let us use the Chebyshev inequality to bound the probability that |X-2≥1. ·We haveσ2=16/12=4/3,and P(IX-2≥1)≤4/3 Which is uninformative. 7
Example 2: Uninformative case • Let 𝑋 be uniformly distributed in 0,4 . • Let us use the Chebyshev inequality to bound the probability that |𝑋 − 2| ≥ 1. • We have 𝜎 2 = 16/12 = 4/3, and 𝑃 |𝑋 − 2 ≥ 1 ≤ 4/3 Which is uninformative. 7

Example 2:Uninformative case let X be exponentially distributed with parameter =1,so that E[X]=var(X)=1. For c 1,using the Chebyshev inequality,we obtain P(x>c)= P(X-1≥c-1) ≤P(X-1≥c-1) 1 ≤ (c-1)2 8
Example 2: Uninformative case • let 𝑋 be exponentially distributed with parameter 𝜆 = 1, so that 𝐸[𝑋] = 𝑣𝑎𝑟(𝑋) = 1. • For 𝑐 > 1, using the Chebyshev inequality, we obtain 𝑃 𝑥 ≥ 𝑐 = 𝑃 𝑋 − 1 ≥ 𝑐 − 1 ≤ 𝑃 𝑋 − 1 ≥ 𝑐 − 1 ≤ 1 𝑐−1 2 8
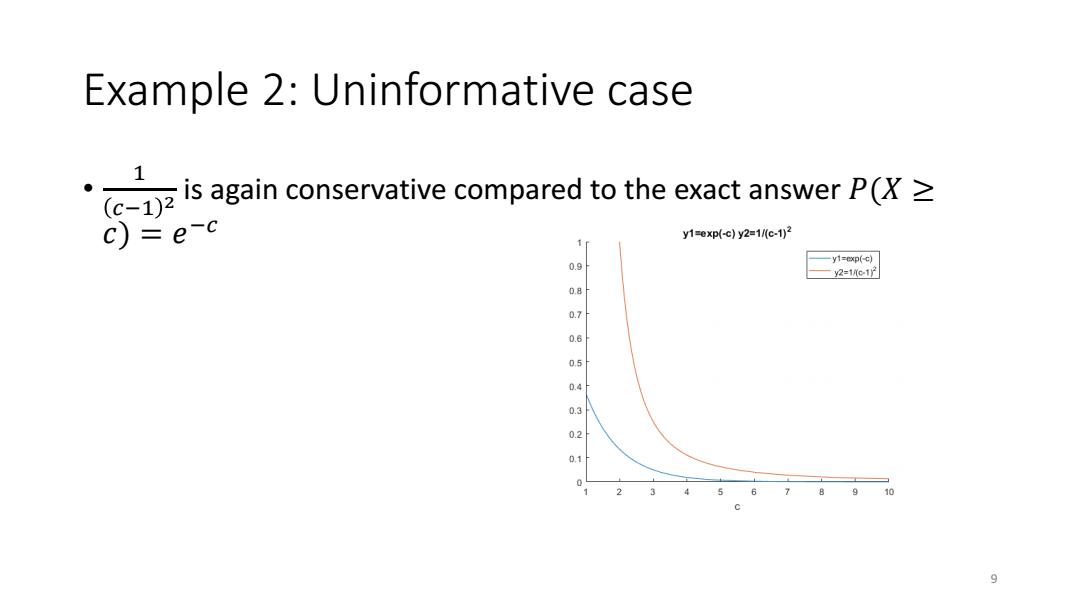
Example 2:Uninformative case is again conservative compared to the exact answer P(> c)=e-c y1=exp(-c)y2=1c-1)2 0.9 一y1=ep(c) y2=1e12 55 0.4 0.3 g10 9
Example 2: Uninformative case • 1 𝑐−1 2 is again conservative compared to the exact answer 𝑃(𝑋 ≥ 𝑐) = 𝑒 −𝑐 9

Weak law of large numbers The law asserts that the sample mean of a large number of independent identically distributed random variables is very close to the true mean,with high probability
Weak law of large numbers • The law asserts that the sample mean of a large number of independent identically distributed random variables is very close to the true mean, with high probability