
ENGG430Protaistics onnrs Chapter 9:Classical Statistical Inference Instructor: Shengyu Zhang
Instructor: Shengyu Zhang

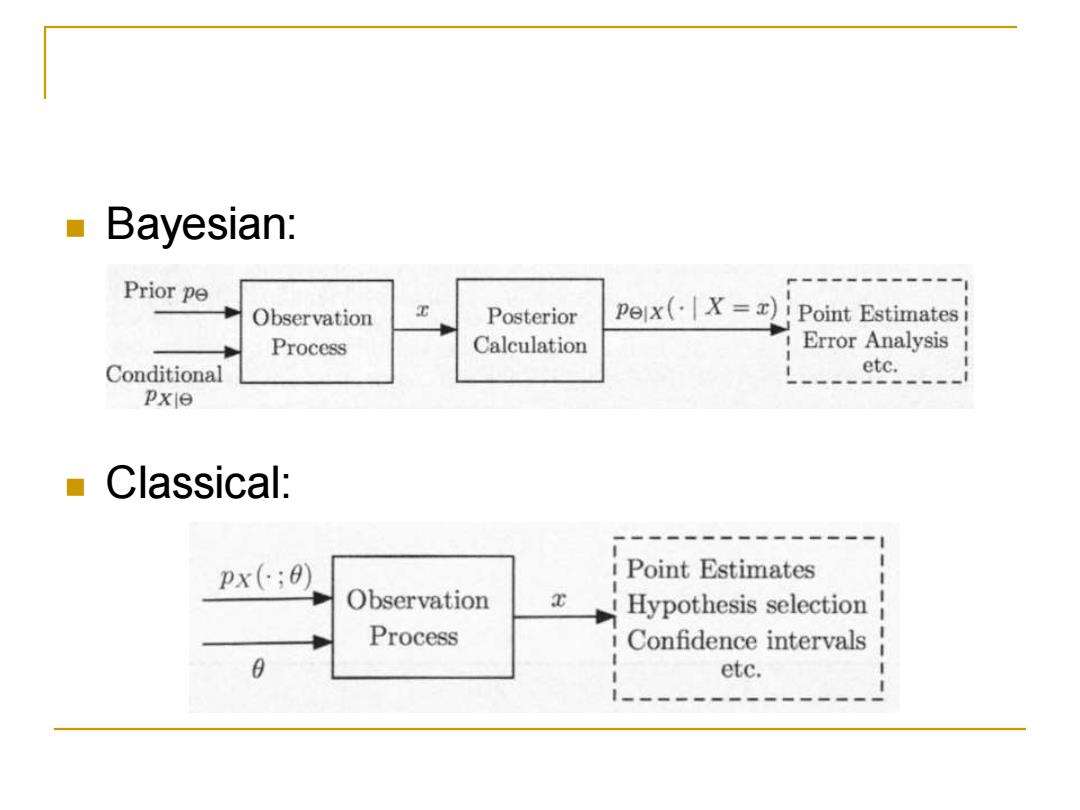
Preceding chapter:Bayesian inference Preceding chapter:Bayesian approach to inference. Unknown parameters are modeled as random variables. a Work within a single,fully-specified probabilistic model. Compute posterior distribution by judicious application of Bayes'rule
Preceding chapter: Bayesian inference ◼ Preceding chapter: Bayesian approach to inference. ❑ Unknown parameters are modeled as random variables. ❑ Work within a single, fully-specified probabilistic model. ❑ Compute posterior distribution by judicious application of Bayes' rule

This chapter:classical inference We view the unknown parameter 0 as a deterministic (not random!)but unknown quantity. The observation X is random and its distribution px(x;0)if X is discrete x(x;0)if X is continuous depends on the value of 0
This chapter: classical inference ◼ We view the unknown parameter 𝜃 as a deterministic (not random!) but unknown quantity. ◼ The observation 𝑋 is random and its distribution ❑ 𝑝𝑋 𝑥; 𝜃 if 𝑋 is discrete ❑ 𝑓𝑋 𝑥; 𝜃 if 𝑋 is continuous depends on the value of 𝜃

Classical inference Deal simultaneously with multiple candidate models,one model for each possible value of 0. A "good"hypothesis testing or estimation procedure will be one that possesses certain desirable properties under every candidate model. ▣i.e.for every possible value ofθ
Classical inference ◼ Deal simultaneously with multiple candidate models, one model for each possible value of 𝜃. ◼ A ''good" hypothesis testing or estimation procedure will be one that possesses certain desirable properties under every candidate model. ❑ i.e. for every possible value of 𝜃
Bayesian: Prior pe Observation Posterior Pex(X=)Point Estimatesi Process Calculation Error Analysis Conditional etc. pxie Classical: px(;0) Point Estimates Observation x Hypothesis selection Process Confidence intervals 8 etc
◼ Bayesian: ◼ Classical:

Notation Our notation will generally indicate the dependence of probabilities and expected values on 0. For example,we will denote by Ee[h()]the expected value of a random variable h()as a function of 0. Similarly,we will use the notation Pe(A)to denote the probability of an event A
Notation ◼ Our notation will generally indicate the dependence of probabilities and expected values on 𝜃. ◼ For example, we will denote by 𝐸𝜃 ℎ 𝑋 the expected value of a random variable ℎ 𝑋 as a function of 𝜃. ◼ Similarly, we will use the notation 𝑃𝜃 𝐴 to denote the probability of an event 𝐴

Content Classical Parameter Estimation ■Linear Regression Binary Hypothesis Testing Significance Testing
Content ◼ Classical Parameter Estimation ◼ Linear Regression ◼ Binary Hypothesis Testing ◼ Significance Testing

Given observations =(X1,...,Xn),an estimator is a random variable of the form 6=g(x),for some function g. Note that since the distribution of X depends on 0,the same is true for the distribution of 6. We use the term estimate to refer to an actual realized value of 6
◼ Given observations 𝑋 = 𝑋1,… ,𝑋𝑛 , an estimator is a random variable of the form Θ = 𝑔 𝑋 , for some function 𝑔. ◼ Note that since the distribution of 𝑋 depends on 𝜃, the same is true for the distribution of Θ . ◼ We use the term estimate to refer to an actual realized value of Θ

■ Sometimes,particularly when we are interested in the role of the number of observations n,we use the notation for an estimator. ■ It is then also appropriate to viewn as a sequence of estimators. One for each value of n. The mean and variance of are denoted Ee[⑥n]and vare[⑥nl,respectively. We sometimes drop this subscript 0 when the context is clear
◼ Sometimes, particularly when we are interested in the role of the number of observations 𝑛, we use the notation Θ𝑛 for an estimator. ◼ It is then also appropriate to view Θ𝑛 as a sequence of estimators. ❑ One for each value of 𝑛. ◼ The mean and variance of Θ 𝑛 are denoted 𝐸𝜃 Θ𝑛 and 𝑣𝑎𝑟𝜃 Θ𝑛 , respectively. ❑ We sometimes drop this subscript 𝜃 when the context is clear

Terminology regarding estimators Estimator:6n,a function of n observations for an (X1,...,Xn)whose distribution depends on 0. Estimation error:n=n-0. Bias of the estimator:be(n=EeOn]-0,is the expected value of the estimation error
Terminology regarding estimators ◼ Estimator: Θ 𝑛, a function of 𝑛 observations for an 𝑋1,… , 𝑋𝑛 whose distribution depends on 𝜃. ◼ Estimation error: Θ෩𝑛 = Θ 𝑛 − 𝜃. ◼ Bias of the estimator: 𝑏𝜃 Θ 𝑛 = 𝐸𝜃 Θ 𝑛 − 𝜃, is the expected value of the estimation error