
Random Walk on Graphs and its Algorithmic Applications Shengyu Zhang Winter School,ITCSC@CUHK,2009
Random Walk on Graphs and its Algorithmic Applications Shengyu Zhang Winter School, ITCSC@CUHK, 2009
Random walk on graphs On an undirected graph G: ■ Starting from vertex vo Repeat for a number of steps: Go to a random neighbor Simple but powerful
Random walk on graphs On an undirected graph G: ◼ Starting from vertex v0 ◼ Repeat for a number of steps: ❑ Go to a random neighbor. ◼ Simple but powerful

Road map:Random walk Parameters Algorithms /Properties ▣k-SAT Hitting time ▣st-connectivity ▣PageRank Mixing time Approximate counting ▣Error-reduction
Road map: Random walk Parameters /Properties Hitting time Algorithms ❑ k-SAT ❑ st-connectivity Mixing time ❑ PageRank ❑ Approximate counting ❑ Error-reduction
Road map:Quantum walk Short intro to math model of quantum mechanics Types Algorithms Discrete QW Element Distinctness Continuous QW Formula Evaluation
Road map: Quantum walk Types Discrete QW Algorithms Element Distinctness Continuous QW Formula Evaluation Short intro to math model of quantum mechanics

PART I.Random Walk Key parameter 1:Hitting time
PART I. Random Walk Key parameter 1: Hitting time
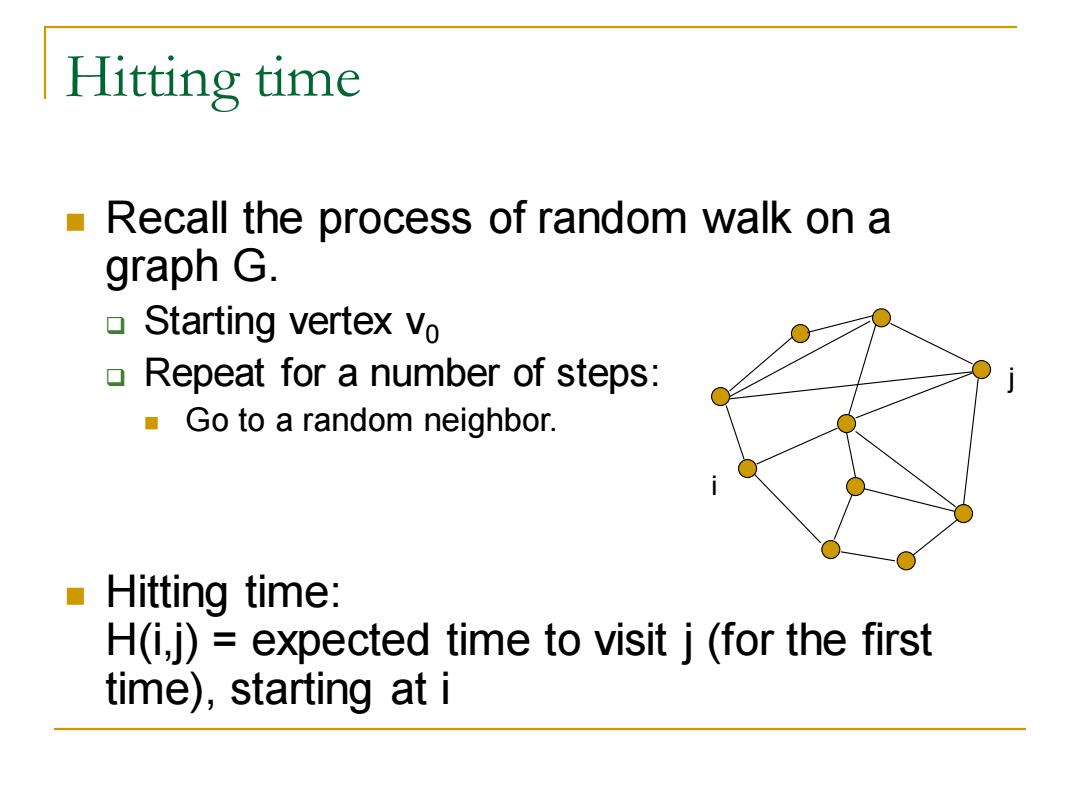
Hitting time Recall the process of random walk on a graph G. Starting vertex vo Repeat for a number of steps: Go to a random neighbor. Hitting t time: H(i,j)=expected time to visit j(for the first time),starting at i
Hitting time ◼ Recall the process of random walk on a graph G. ❑ Starting vertex v0 ❑ Repeat for a number of steps: ◼ Go to a random neighbor. ◼ Hitting time: H(i,j) = expected time to visit j (for the first time), starting at i i j
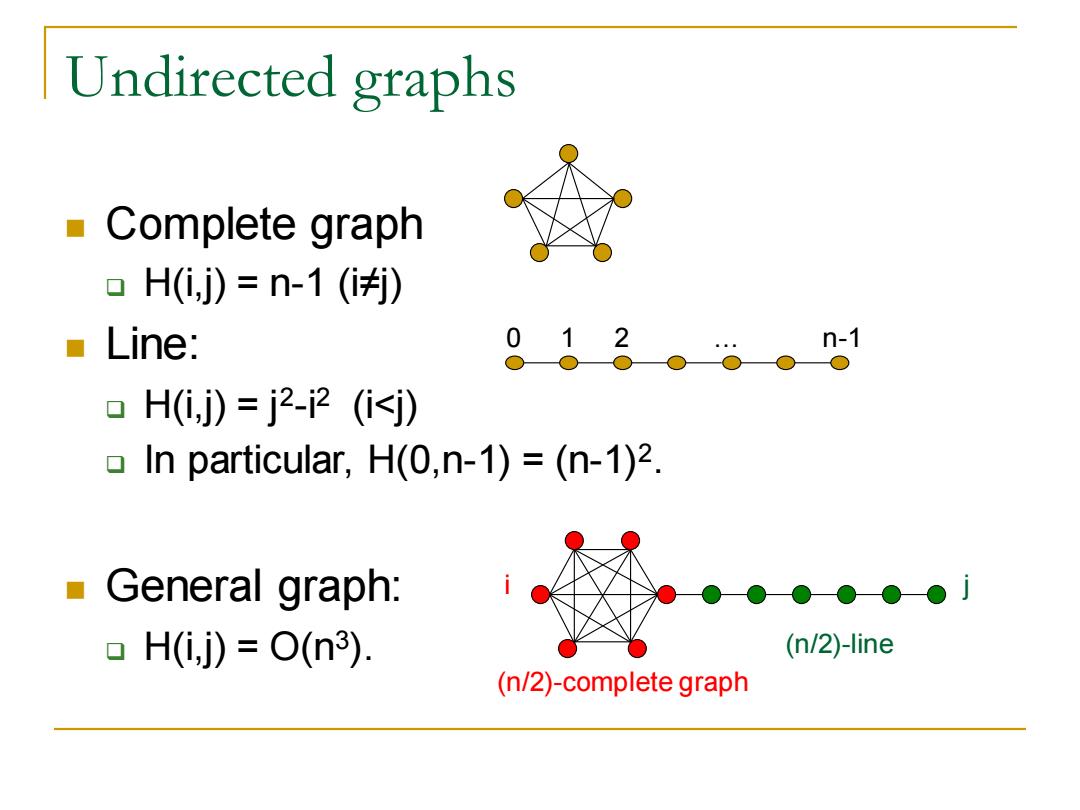
Undirected graphs Complete graph ▣H(i,j)=n-1(i) Line: 0 1 2 n-1 口H(i,j)=j2-2(i≤j) In particular,H(O,n-1)=(n-1)2. General graph: ▣H(,j)=O(n3). (n/2)-line (n/2)-complete graph
Undirected graphs ◼ Complete graph ❑ H(i,j) = n-1 (i≠j) ◼ Line: ❑ H(i,j) = j2 -i 2 (i<j) ❑ In particular, H(0,n-1) = (n-1)2 . ◼ General graph: ❑ H(i,j) = O(n3 ). 0 1 2 … n-1 (n/2)-complete graph (n/2)-line i j

Algorithm 1:2-SAT
Algorithm 1: 2-SAT

k-SAT:satisfiability of k-CNF formula n variables x1,...xE0,1) m clauses,each being OR of k literals Literal:Xi or x 口e.g.(k=3):(x1)vX5vX7 3-CNF formula:AND of these m clauses 口e.g.(口x1)vx5YX)(2v(xs)Y(x7)(X1v7Y8) 3-SAT Problem:Given a 3CNF formula,decide whether there is an assignment ofvariables s.t.the formula evaluates to 1. For the above example,Yes:X5=1,X7=0,x1=1
k-SAT: satisfiability of k-CNF formula ◼ n variables x1 , …, xn∊{0,1} ◼ m clauses, each being OR of k literals ❑ Literal: xi or ¬xi ❑ e.g. (k=3): (¬x1 ) ٧ x5 ٧ x7 ◼ 3-CNF formula: AND of these m clauses ❑ e.g. ((¬x1 ) ٧ x5 ٧ x7 ) ٨ (x2 ٧ (¬x5 ) ٧ (¬x7 )) ٨ (x1 ٧ x7 ٧ x8 ) ◼ 3-SAT Problem: Given a 3CNF formula, decide whether there is an assignment of variables s.t. the formula evaluates to 1. ❑ For the above example, Yes: x5=1, x7=0, x1=1

P vs.NP P:problems that can be easily solved a“easily”:in polynomial time NP:problems that can be easily verified. Formally:3 a polynomial time verifier V,s.t.for any input x, If the answer is YES,then 3y s.t.V(x,y)=1 If the answer is NO,then Vy,V(x,y)=1 The question of TCS:Is P NP? Intuitively,no.NP should be much larger. It's much easier to verify(with help)than to solve(by yourself) mathematical proof,appreciation of good music/food,... Formal proof?We don't know yet. One of the 7 Millennium Problems by CMI. 1http://www.claymath.org/millennium/P_vs_NP/
P vs. NP ◼ P: problems that can be easily solved ❑ “easily”: in polynomial time ◼ NP: problems that can be easily verified. ❑ Formally: ∃ a polynomial time verifier V, s.t. for any input x, ◼ If the answer is YES, then ∃y s.t. V(x,y) = 1 ◼ If the answer is NO, then ∀y, V(x,y) = 1 ◼ The question of TCS: Is P = NP? ❑ Intuitively, no. NP should be much larger. ◼ It’s much easier to verify (with help) than to solve (by yourself) ◼ mathematical proof, appreciation of good music/food, … ❑ Formal proof? We don’t know yet. ◼ One of the 7 Millennium Problems by CMI.① ① http://www.claymath.org/millennium/P_vs_NP/