
n the powerftchnfor 1way uantumcation complexity Shengyu Zhang The Chinese University of Hong Kong
Shengyu Zhang The Chinese University of Hong Kong
Algorithms Circuit Ib Info.theory 0 Streaming Algorithms Quantum Communication crypto Computing O0 Complexity" VLSI Data games Structures Question:What's the largest gap between classical and quantum communication complexities?
Quantum Computing Communication Complexity Question: What’s the largest gap between classical and quantum communication complexities? Algorithms Info. theory crypto games … Circuit lb Streaming Algorithms VLSI Data Structures …
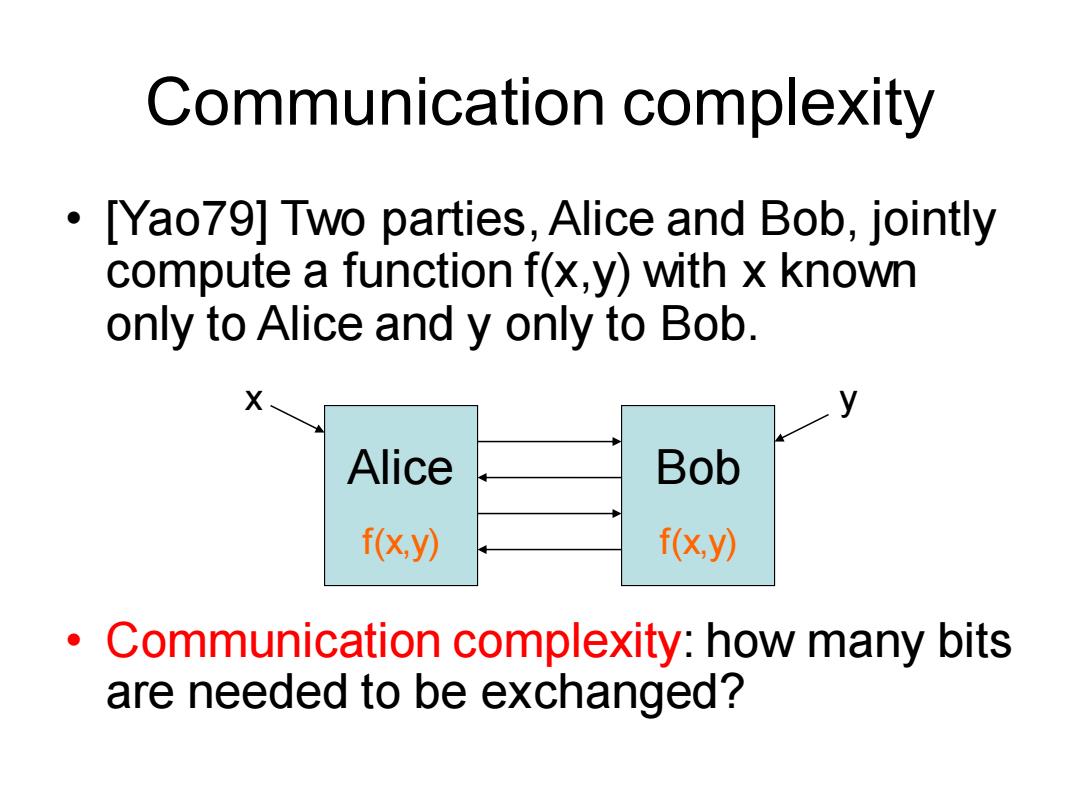
Communication complexity [Yao79]Two parties,Alice and Bob,jointly compute a function f(x,y)with x known only to Alice and y only to Bob. Alice Bob f(x,y) f(xy) Communication complexity:how many bits are needed to be exchanged?
Communication complexity • [Yao79] Two parties, Alice and Bob, jointly compute a function f(x,y) with x known only to Alice and y only to Bob. • Communication complexity: how many bits are needed to be exchanged? Alice Bob f(x,y) f(x,y) x y

Various protocols ·Deterministic:D(f 。Randomized:R(f -A bounded error probability is allowed. -Private or public coins?Differ by +O(log n). Quantum:Q(f) -A bounded error probability is allowed. -Assumption:No shared Entanglement. (Does it help?Open.)
Various protocols • Deterministic: D(f) • Randomized: R(f) – A bounded error probability is allowed. – Private or public coins? Differ by ±O(log n). • Quantum: Q(f) – A bounded error probability is allowed. – Assumption: No shared Entanglement. (Does it help? Open.)

Communication complexity: one-way model X Alice Bob f(x,y) One-way:Alice sends a message to Bob. -D1(⑤,R1(⑤,Q1(⑤
Communication complexity: one-way model • One-way: Alice sends a message to Bob. --- D1 (f), R1 (f), Q1 (f) Alice Bob x y f(x,y)

About one-way model ·Power: As efficient as the best two-way protocol. -Efficient protocols for specific functions s such as Equality,Hamming Distance,and in general,all symmetric XOR functions. 。Applications: Lower bound for space complexity of streaming algorithms. Lower bound?Can be quite hard, especially for quantum
About one-way model • Power: – Efficient protocols for specific functions such as Equality, Hamming Distance, and in general, all symmetric XOR functions. • Applications: – Lower bound for space complexity of streaming algorithms. • Lower bound? Can be quite hard, especially for quantum. As efficient as the best two-way protocol

Question Question:What's the largest gap between classical and quantum communication complexities? Partial functions,relations:exponential. Total functions,two-way: -Largest gap:Q(Disj)=e(Vn),R(Disj)=e(n) -Best bound:R(f)=exp(Q(f)). ·Conjecture:R(f=poly(Q(f⑤):
Question • Question: What’s the largest gap between classical and quantum communication complexities? • Partial functions, relations: exponential. • Total functions, two-way: – Largest gap: Q(Disj) = Θ(√n), R(Disj) = Θ(n). – Best bound: R(f) = exp(Q(f)). • Conjecture: R(f) = poly(Q(f))

Question Question:What's the largest gap between classical and quantum communication complexities? Partial functions,relations:exponential. Total functions,one-way: Largest gap:R1(EQ)=2.Q1(EQ), -Best bound:R1(⑤=exp(Q1(⑤): ·Conjecture:R1(f⑤=poly(Q'(f), -or even R1(⑤=O(Q1(⑤):
Question • Question: What’s the largest gap between classical and quantum communication complexities? • Partial functions, relations: exponential. • Total functions, one-way: – Largest gap: R1 (EQ) = 2∙Q1 (EQ), – Best bound: R1 (f) = exp(Q1 (f)). • Conjecture: R1 (f) = poly(Q1 (f)), – or even R1 (f) = O(Q1 (f))

Approaches Approach 1:Directly simulate a quantum protocol by classical one. [Aaronson]R1(f)=O(m-Q1(f)). ·Approach2:L(⑤≤Q1(⑤≤R1(⑤≤poly(L(f). -[Nayak99;Jain,Z.'09]R1(f)=O(IVC(f)),where lu is the mutual info of any hard distribution u. Note:For the approach 2 to be possibly succeed, the quantum lower bound L(f)has to be polynomially tight for Q1(f)
Approaches • Approach 1: Directly simulate a quantum protocol by classical one. – [Aaronson] R1 (f) = O(m∙Q1 (f)). • Approach 2: L(f) ≤ Q1 (f) ≤ R1 (f) ≤ poly(L(f)). – [Nayak99; Jain, Z.’09] R1 (f) = O(Iμ ∙VC(f)), where Iμ is the mutual info of any hard distribution μ. • Note: For the approach 2 to be possibly succeed, the quantum lower bound L(f) has to be polynomially tight for Q1 (f)

Main result There are three lower bound techniques known forQ1(⑤. Nayak'99:Partition Tree Aaronson'05:Trace Distance The two-way complexity Q(f) [Thm]All of these lower bounds can be arbitrarily weak. Actually,random functions have Q(f)=(n),but the first two lower bounds only give O(1)
Main result • There are three lower bound techniques known for Q1 (f). – Nayak’99: Partition Tree – Aaronson’05: Trace Distance – The two-way complexity Q(f) • [Thm] All of these lower bounds can be arbitrarily weak. • Actually, random functions have Q(f) = Ω(n), but the first two lower bounds only give O(1)