
Tutorial 2:Sample Space and Probability 2 Baoxiang WANG bxwang@cse Spring 2017
Tutorial 2: Sample Space and Probability 2 Baoxiang WANG bxwang@cse Spring 2017

Probability models A probability model is an assignment of probabilities to every element of the sample space. Probabilities are nonnegative and add up to one. Examples S=HH,HT,TH,TT /44/4/4 107 models a pair of coins with equally likely outcomes
Probability models A probability model is an assignment of probabilities to every element of the sample space. Probabilities are nonnegative and add up to one. S = { HH, HT, TH, TT } ¼ ¼ ¼ ¼ Examples models a pair of coins with equally likely outcomes

Elements of a Probabilistic Model Event:a subset of sample space. -A is a set of possible outcomes -Example.A ={HH,T'T},the event that the two coins give the same side. The probability law assigns our knowledge or belief to an event Aa number P(A)0. It specifies the likelihood of any outcome
Elements of a Probabilistic Model • Event: a subset of sample space. – 𝐴 ⊆ Ω is a set of possible outcomes – Example. 𝐴 = 𝐻𝐻, 𝑇𝑇 , the event that the two coins give the same side. • The probability law assigns our knowledge or belief to an event 𝐴 a number 𝑃 𝐴 ≥ 0. – It specifies the likelihood of any outcome

Probability Axioms 1.(Won-negativity)P(A)≥0,for every event A. 2.(Additivity)For any two disjoint events A and B,P(AUB)=P(A)+P(B) In general,if A1,A2,..are disjoint events, then P(A1UA2U…)=P(A1)+P(A2)+… 3.(Normalization)P()=1
Probability Axioms 1. (Non-negativity) 𝑃(𝐴) ≥ 0, for every event 𝐴. 2. (Additivity) For any two disjoint events 𝐴 and 𝐵, 𝑃 𝐴 ∪ 𝐵 = 𝑃 𝐴 + 𝑃 𝐵 In general, if 𝐴1, 𝐴2, … are disjoint events, then 𝑃 𝐴1 ∪ 𝐴2 ∪ ⋯ = 𝑃 𝐴1 + 𝑃 𝐴2 + ⋯ 3. (Normalization) 𝑃(Ω) = 1
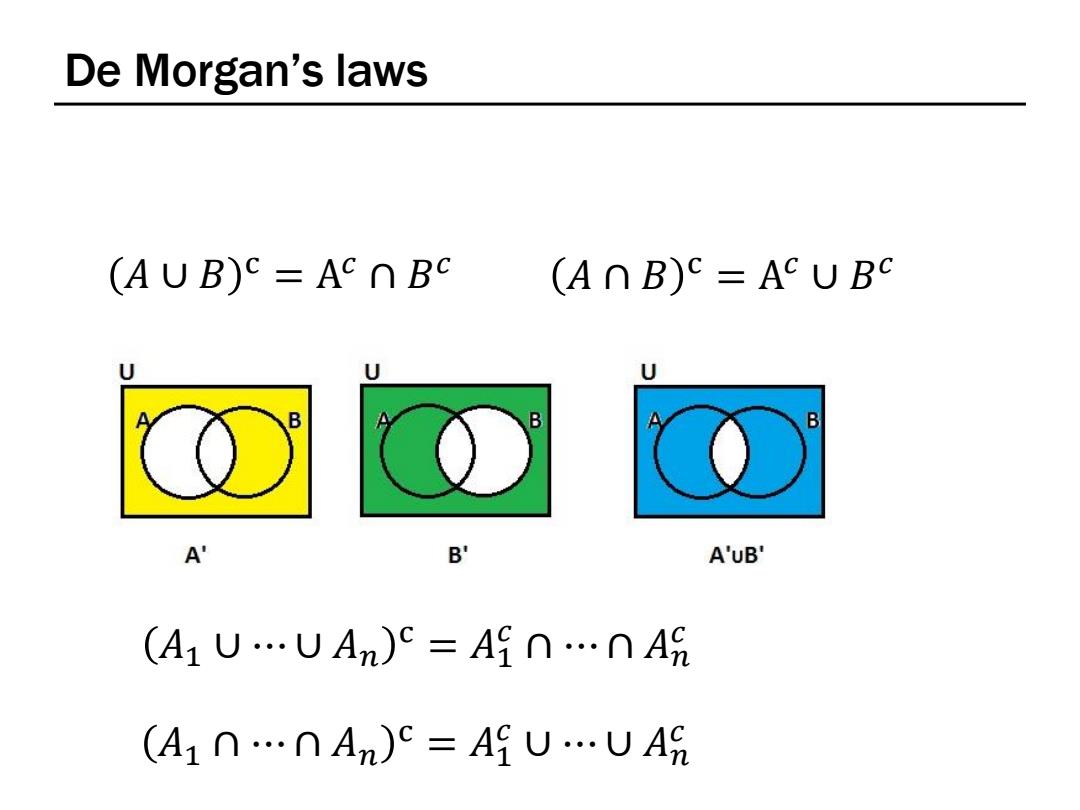
De Morgan's laws (AUB)c=AC∩Bc (AnB)C=ACUB U U B B B A' B' A'uB' (A1UUAn)C=An…nA8 (A1n…nAn)c=AUUA9
De Morgan’s laws 𝐴 ∪ 𝐵 c = A 𝑐 ∩ 𝐵 𝑐 𝐴 ∩ 𝐵 c = A 𝑐 ∪ 𝐵 𝑐 𝐴1 ∪ ⋯ ∪ 𝐴𝑛 c = 𝐴1 𝑐 ∩ ⋯ ∩ 𝐴𝑛 𝑐 𝐴1 ∩ ⋯ ∩ 𝐴𝑛 c = 𝐴1 𝑐 ∪ ⋯ ∪ 𝐴𝑛 𝑐

Question Bonferroni's inequality. Prove that for any two events a and B,we have P(A∩B)≥P(A)+P(B)-1 P(A)+P(B)-P(AnB)=P(AUB) P(AUB)≤1 A AnB B
Question Bonferroni’s inequality. Prove that for any two events A and B, we have 𝑃 𝐴 ∩ 𝐵 ≥ 𝑃 𝐴 + 𝑃 𝐵 − 1 𝑃 𝐴 + 𝑃 𝐵 − 𝑃 𝐴 ∩ 𝐵 = 𝑃(𝐴 ∪ 𝐵) 𝑃(𝐴 ∪ 𝐵) ≤ 1

Question Romeo and Juliet have a date. Each will arrive at the meeting place with a delay between 0 and 1 hour,with all pairs of delays being equally likely. The first to arrive will wait for 15 minutes and will leave if the other has not yet arrived. Question:What is the probability that they will meet?
Question Romeo and Juliet have a date. Each will arrive at the meeting place with a delay between 0 and 1 hour, with all pairs of delays being equally likely. The first to arrive will wait for 15 minutes and will leave if the other has not yet arrived. Question: What is the probability that they will meet?

Question Sample space:the unit square[0,1]×[0,1], Its elements are the possible pairs of delays. 1/4 “equally likely”pairs of delays:let P(A)for event 0 1/4 A∈几be equal to A's=kzmk-ns0sx≤10sy= “area”. This satisfies the axioms
Question Sample space: the unit square 0,1 × 0,1 , Its elements are the possible pairs of delays. “equally likely” pairs of delays: let 𝑃 𝐴 for event 𝐴 ⊆ Ω be equal to 𝐴’s “area”. This satisfies the axioms. 𝑀 = 𝑥, 𝑦 : 𝑥 − 𝑦 ≤ 1 4 , 0 ≤ 𝑥 ≤ 1, 0 ≤ 𝑦 ≤ 1
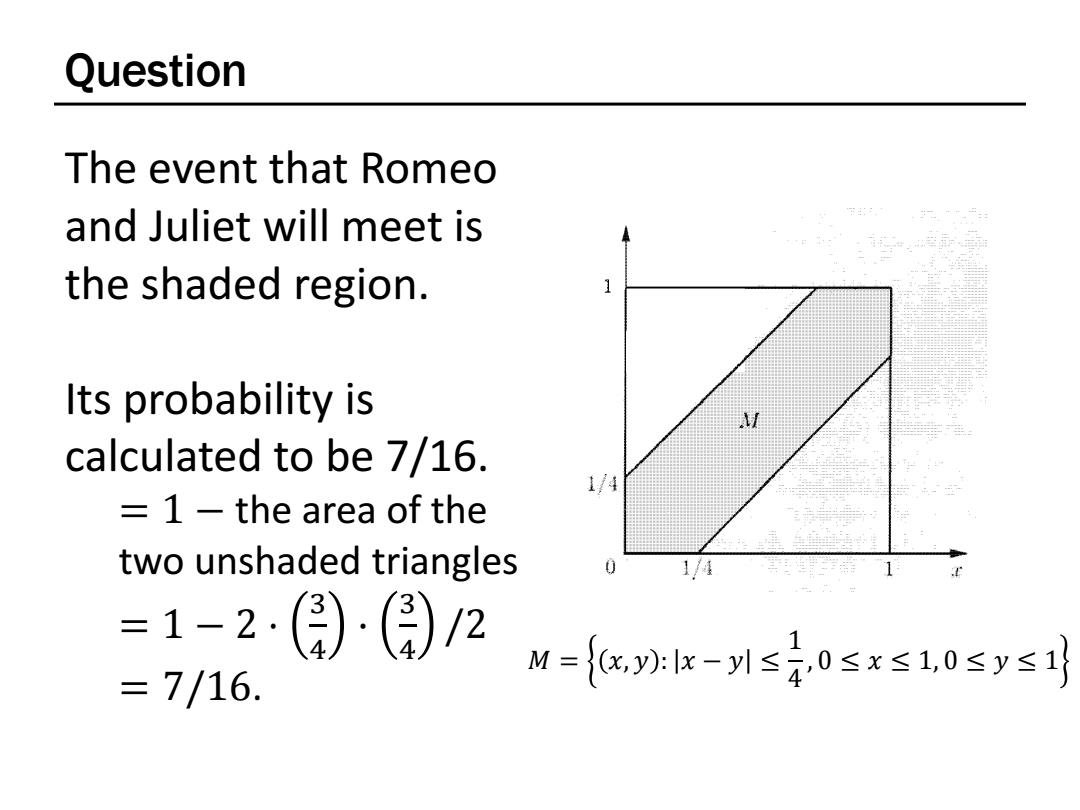
Question The event that Romeo and Juliet will meet is the shaded region. Its probability is calculated to be 7/16. 1/4 1 -the area of the two unshaded triangles 0 1/4 =1-2()()2 =7/16. M={c,wx-1≤0≤x≤1,0≤y≤1
Question The event that Romeo and Juliet will meet is the shaded region. Its probability is calculated to be 7/16. = 1 − the area of the two unshaded triangles = 1 − 2 ⋅ 3 4 · 3 4 /2 = 7/16. 𝑀 = 𝑥, 𝑦 : 𝑥 − 𝑦 ≤ 1 4 , 0 ≤ 𝑥 ≤ 1, 0 ≤ 𝑦 ≤ 1

Question A parking lot contains 100 cars,k of which happen to be lemons.We select m of these cars at random and take them for a test drive.Find the probability that n of the cars tested turn out to be lemons. The sample space frandom choose m cars} The size of sample space
Question A parking lot contains 100 cars, 𝑘 of which happen to be lemons. We select 𝑚 of these cars at random and take them for a test drive. Find the probability that 𝑛 of the cars tested turn out to be lemons. The sample space Ω = random choose 𝑚 cars The size of sample space |Ω| = 100 𝑚