
Tutorial 7:General Random Variables 3 Yitong Meng March 13,2017 1
Tutorial 7: General Random Variables 3 Yitong Meng March 13, 2017 1

Revise-Joint PDF Two continuous random variables X,Y satisfying P((x.Y)EB)=fr(x.)dxdy (X,y)∈B for every subset B
Revise - Joint PDF ◼ Two continuous random variables 𝑋, 𝑌 satisfying 𝑃 𝑋, 𝑌 ∈ 𝐵 = ඵ (𝑥,𝑦)∈𝐵 𝑓𝑋,𝑌 𝑥, 𝑦 𝑑𝑥𝑑𝑦 for every subset 𝐵

Revise-Marginal Probability ·P(X∈A)=P(X∈A,Y∈(-∞,∞) =∫rx妙r 0∞ The marginal PDF of X is 00 fx(x)=fx.v(x.y)dy
Revise - Marginal Probability ◼ 𝑃 𝑋 ∈ 𝐴 = 𝑃 𝑋 ∈ 𝐴, 𝑌 ∈ −∞, ∞ = න 𝐴 න −∞ ∞ 𝑓𝑋,𝑌 𝑥, 𝑦 𝑑𝑦 𝑑𝑥 ◼ The marginal PDF of 𝑋 is 𝑓𝑋 𝑥 = න −∞ ∞ 𝑓𝑋,𝑌 𝑥, 𝑦 𝑑𝑦

Example:Buffon's Needle A surface is ruled with parallel lines,which at distance d from each other. Suppose we throw a needle of length l randomly. What is the prob.that the needle will intersect one of the lines?
Example: Buffon’s Needle ◼ A surface is ruled with parallel lines, which at distance 𝑑 from each other. ◼ Suppose we throw a needle of length 𝑙 randomly. ◼ What is the prob. that the needle will intersect one of the lines?

Example:Buffon's Needle -Assume l<d so that the needle cannot intersect two lines simultaneously. X,the distance from the middle point of the needle and the nearest of the parallel lines 9,the acute angle formed by the needle and the lines
Example: Buffon’s Needle ◼ Assume 𝑙 < 𝑑 so that the needle cannot intersect two lines simultaneously. ◼ 𝑋, the distance from the middle point of the needle and the nearest of the parallel lines ◼ 𝜗, the acute angle formed by the needle and the lines

Example:Buffon's Needle We model (X,)with a uniform joint PDF so that 4 fre到midc3 otherwise
Example: Buffon’s Needle ◼ We model (𝑋, 𝜗) with a uniform joint PDF so that 𝑓𝑋,𝜗 𝑥, 𝜃 = ൞ 4 𝜋𝑑 , 𝑖𝑓 𝑥 ∈ 0, 𝑑 2 𝑎𝑛𝑑 𝜃 ∈ [0, 𝜋 2 ] 0, 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒
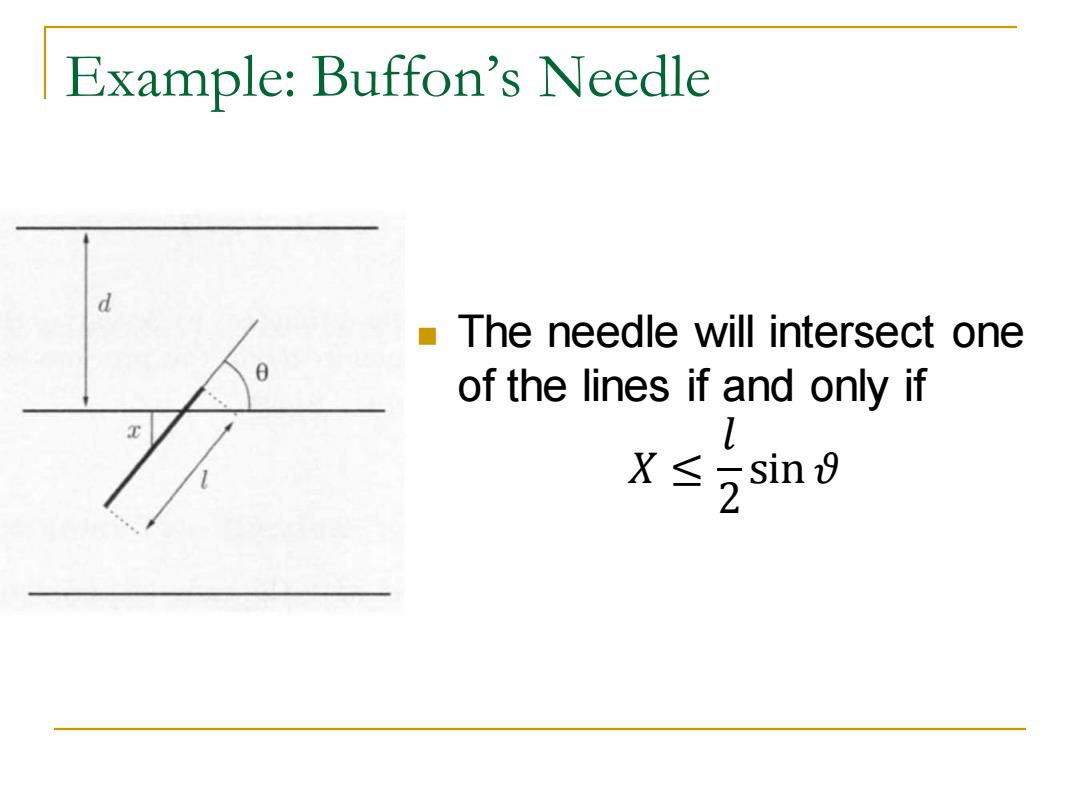
Example:Buffon's Needle The needle will intersect one of the lines if and only if X≤ sin
Example: Buffon’s Needle ◼ The needle will intersect one of the lines if and only if 𝑋 ≤ 𝑙 2 sin 𝜗

Example:Buffon's Needle So the probability of intersection is p《m- x(x,)dxde 4 sin 0 二 πd xde= -月 21 21
Example: Buffon’s Needle ◼ So the probability of intersection is 𝑃 𝑋 ≤ 𝑙 2 sin 𝜗 = ඵ 𝑋≤ 𝑙 2 sin 𝜃 𝑓𝑋,𝜗 𝑥, 𝜃 𝑑𝑥𝑑𝜃 = 4 𝜋𝑑 න 0 𝜋/2 න 0 𝑙 2 sin 𝜃 𝑑𝑥𝑑𝜃 = 4 𝜋𝑑 න 0 𝜋/2 𝑙 2 sin 𝜃 𝑑𝜃 = 2𝑙 𝜋𝑑 − cos 𝜃 อ 𝜋 2 0 = 2𝑙 𝜋𝑑

Example:Multivariate Gaussian Let X E R be a n-dimensional normal random variable.The PDF of X is then 1 -2x-w)TΣ-1(x-W) fx(x)= n.1 (2π)22
Example: Multivariate Gaussian ◼ Let 𝑋 ∈ 𝑅 𝑛 be a n-dimensional normal random variable. The PDF of 𝑋 is then 𝑓𝑋 𝑥 = 1 2𝜋 𝑛 2 Σ 1 2 − 1 2 𝑥−𝜇 𝑇Σ −1 𝑥−𝜇

Example:Multivariate Gaussian The mean and variance E(X) V(X)= (Recall) 1 -2x-w)TΣ-1(x-wW fx(x)= n 1 (2π)22
Example: Multivariate Gaussian ◼ The mean and variance 𝐸 𝑋 = 𝜇 𝑉 𝑋 = Σ (Recall) 𝑓𝑋 𝑥 = 1 2𝜋 𝑛 2 Σ 1 2 − 1 2 𝑥−𝜇 𝑇Σ −1 𝑥−𝜇