
Networked Fairness in Cake Cutting Xiaohui Bei Youming Qiao Shengyu Zhang
Networked Fairness in Cake Cutting Xiaohui Bei Youming Qiao Shengyu Zhang

Economics In a nutshell,economics studies how resources are managed and allocated. One of the most fundamental targets is to achieve certain fairness in the allocation of resources
Economics • In a nutshell, economics studies how resources are managed and allocated. • One of the most fundamental targets is to achieve certain fairness in the allocation of resources

Cake cutting ·Problem setting: One cake,n people (who want to split it). Each person might value different portions of the cake differently. Some like strawberries,some like chocolate,.. Normalization:Each one values the whole cake as 1. This valuation info is private. Goal:divide the cake to make all people happy
Cake cutting • Problem setting: • One cake, 𝑛 people (who want to split it). • Each person might value different portions of the cake differently. • Some like strawberries, some like chocolate, … • Normalization: Each one values the whole cake as 1. • This valuation info is private. • Goal: divide the cake to make all people happy

Cake cutting A cake cutting protocol is proportionally fair (or proportional for short)if each person gets =1/n fraction by her measure. No matter how other people behave. A cake cutting protocol is envy-free if each person thinks that she gets the most by her measure. 。Eny-free→proportional: aij:how much person j gets in person i's measure. ·Envy-free:ai≥ai,j→ proportional:aii >1/n,Vi
Cake cutting • A cake cutting protocol is proportionally fair (or proportional for short) if each person gets ≥ 1/𝑛 fraction by her measure. • No matter how other people behave. • A cake cutting protocol is envy-free if each person thinks that she gets the most by her measure. • Envy-free ⇒ proportional: • 𝑎𝑖𝑗 : how much person 𝑗 gets in person 𝑖’s measure. • Envy-free: 𝑎𝑖𝑖 ≥ 𝑎𝑖𝑗 , ∀𝑗 ⇒ proportional: 𝑎𝑖𝑖 ≥ 1/𝑛, ∀𝑖
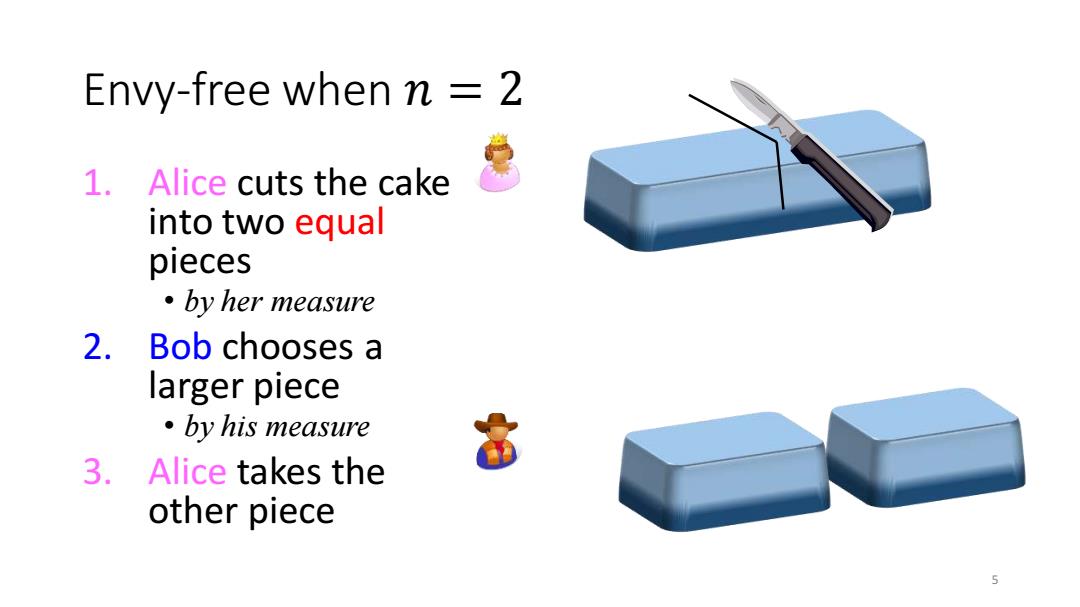
Envy-free when n 2 1.Alice cuts the cake into two equal pieces ·by her measure 2.Bob chooses a larger piece ·by his measure 常 3.Alice takes the other piece 5
5 Envy -free when 𝑛 = 2 1. Alice cuts the cake into two equal pieces • by her measure 2. Bob chooses a larger piece • by his measure 3. Alice takes the other piece

Theorem.The outcome is envy-free (and thus proportionally fair). ●Proof. Alice:gets exactly half no matter which piece Bob chooses, as the two pieces are equal to her. Bob:gets at least half, no matter how Alice cuts the cake, as Bob takes a piece before Alice
• Theorem. The outcome is envy-free (and thus proportionally fair). • Proof. • Alice: gets exactly half • no matter which piece Bob chooses, • as the two pieces are equal to her. • Bob: gets at least half, • no matter how Alice cuts the cake, • as Bob takes a piece before Alice

General n Much more complicated. Only recently*1:discovered a finite-step procedure for finding an envy-free allocation. But the procedure is very complicated. And its complexity is an exponential tower of height 6: *1.Haris Aziz and Simon Mackenzie.A discrete and bounded envy-free cake cutting protocol for any number of agents. F0CS,2016
General 𝑛 • Much more complicated. • Only recently*1 : discovered a finite-step procedure for finding an envy-free allocation. • But the procedure is very complicated. • And its complexity is an exponential tower of height 6: 𝑛 𝑛 𝑛 𝑛 𝑛 𝑛 . *1. Haris Aziz and Simon Mackenzie. A discrete and bounded envy-free cake cutting protocol for any number of agents. FOCS, 2016

Envy on networks Envy usually happens between people knowing each other. We don't envy someone we don't even know. ·Envy on networks: An undirected graph G=(V,E). ·V={agents} ·(i,j)∈E if agent i knows agent j: An allocation is envy-free on G if no agent envies any of her neighbors. An allocation is proportional on G if each agent gets at least the average of her neighbors'total allocation with respect to her own valuation
Envy on networks • Envy usually happens between people knowing each other. • We don’t envy someone we don’t even know. • Envy on networks: • An undirected graph 𝐺 = 𝑉, 𝐸 . • 𝑉 = 𝑎𝑔𝑒𝑛𝑡𝑠 • 𝑖,𝑗 ∈ 𝐸 if agent 𝑖 knows agent 𝑗. • An allocation is envy-free on 𝐺 if no agent envies any of her neighbors. • An allocation is proportional on 𝐺 if each agent gets at least the average of her neighbors’ total allocation • with respect to her own valuation

Observations Envy-free on G → proportional on G 业 业 Envy-free on subgraph G proportional on subgraph G' The standard envy-free is envy-free on the complete graph. Fair allocations on general graphs is not easy,but on special classes of graphs may be. Goal:Simple protocols for fair allocations on certain types ofgraphs. This paper:two classes of graphs
Observations • Envy-free on 𝐺 ⇒ proportional on 𝐺 ⇓ ⇓ Envy-free on subgraph 𝐺 ′ ⇒ proportional on subgraph 𝐺 ′ • The standard envy-free is envy-free on the complete graph. • Fair allocations on general graphs is not easy, but on special classes of graphs may be. • Goal: Simple protocols for fair allocations on certain types of graphs. • This paper: two classes of graphs

First class:trees Theorem 1.For any tree T,there is a procedure to output an allocation that is envy-free on T. An useful algorithm*1:AustinCut(i,j,m,S) i,j:two agents.m:positive integer.S:part of cake. AustinCut(i,j,m,S)cuts S into n pieces so that both agent i and agent j view them all equal. ·(S)==(Sn)=S) ·(S1)=…=(Sm)=(S) *1.AK Austin.Sharing a cake.The Mathematical Gazette,66(437):212-215,1982
First class: trees • Theorem 1. For any tree 𝑇, there is a procedure to output an allocation that is envy-free on 𝑇. • An useful algorithm*1 : AustinCut 𝑖,𝑗, 𝑚, 𝑆 • 𝑖,𝑗: two agents. 𝑚: positive integer. 𝑆: part of cake. • AustinCut 𝑖,𝑗, 𝑚, 𝑆 cuts 𝑆 into 𝑛 pieces so that both agent 𝑖 and agent 𝑗 view them all equal. • 𝑣𝑖 𝑆1 = ⋯ = 𝑣𝑖 𝑆𝑛 = 1 𝑛 𝑣𝑖 𝑆 • 𝑣𝑗 𝑆1 = ⋯ = 𝑣𝑗 𝑆𝑛 = 1 𝑛 𝑣𝑗 𝑆 *1. AK Austin. Sharing a cake. The Mathematical Gazette, 66(437):212–215, 1982