
CSC3160: Design and Analysis of Algorithms Week 2: Single Source Shortest Paths Instructor: Shengyu Zhang
Instructor: Shengyu Zhang

Content Graphs:model,size,distance. Problem:shortest path Algorithms: BFS:unweighted Dijkstra:non-negative weights 0 Bellman-Ford:negative weights 2
Content ◼ Graphs: model, size, distance. ◼ Problem: shortest path. ◼ Algorithms: ❑ BFS: unweighted ❑ Dijkstra: non-negative weights ❑ Bellman-Ford: negative weights 2
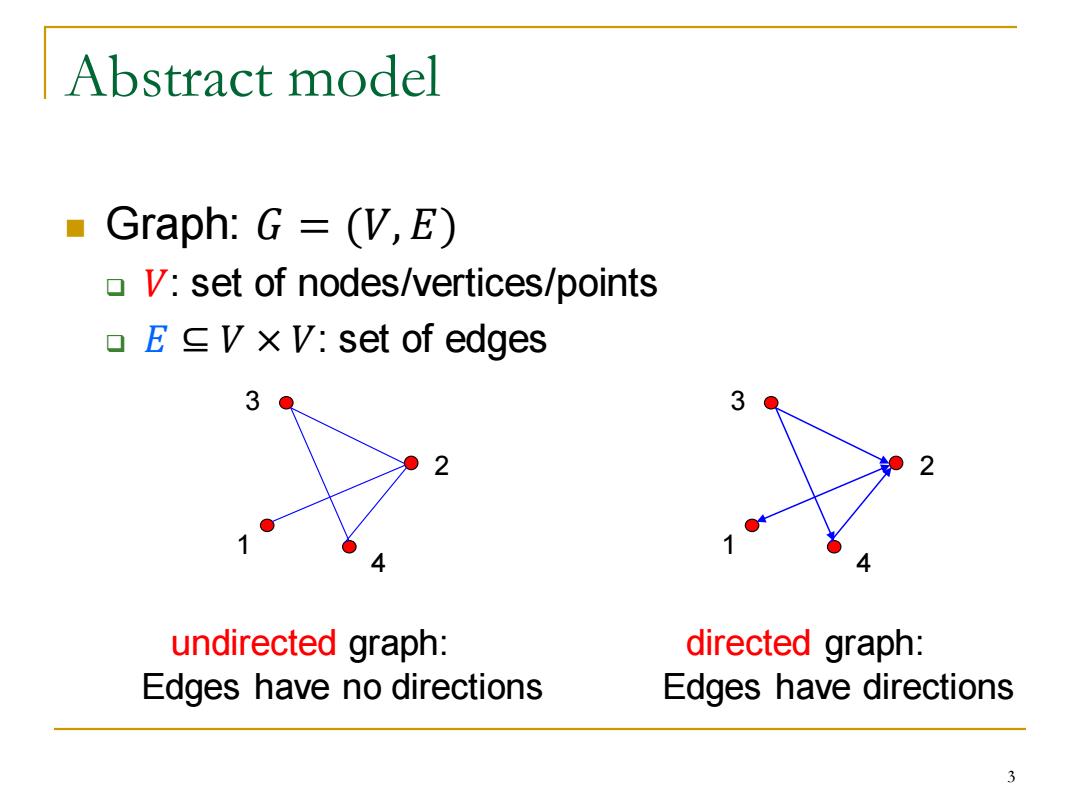
Abstract model ·Graph:G=(V,E) V:set of nodes/vertices/points EV xV:set of edges 3 3 undirected graph: directed graph: Edges have no directions Edges have directions 3
Abstract model ◼ Graph: 𝐺 = (𝑉, 𝐸) ❑ 𝑉: set of nodes/vertices/points ❑ 𝐸 ⊆ 𝑉 × 𝑉: set of edges 3 1 2 4 undirected graph: Edges have no directions directed graph: Edges have directions 3 1 2 4 3

Graph,graph,graph... Why graph?There are lots of graph examples in our lives. Name one. Information:W.citation Social:co-actor,dating,messenger,communities Technological:Internet,power grids,airline routes Biological:Neural networks,food web,blood vessels
Graph, graph, graph… ◼ Why graph? There are lots of graph examples in our lives. ◼ Name one. ❑ Information: WWW, citation ❑ Social: co-actor, dating, messenger, communities ❑ Technological: Internet, power grids, airline routes ❑ Biological: Neural networks, food web, blood vessels ❑ … 4
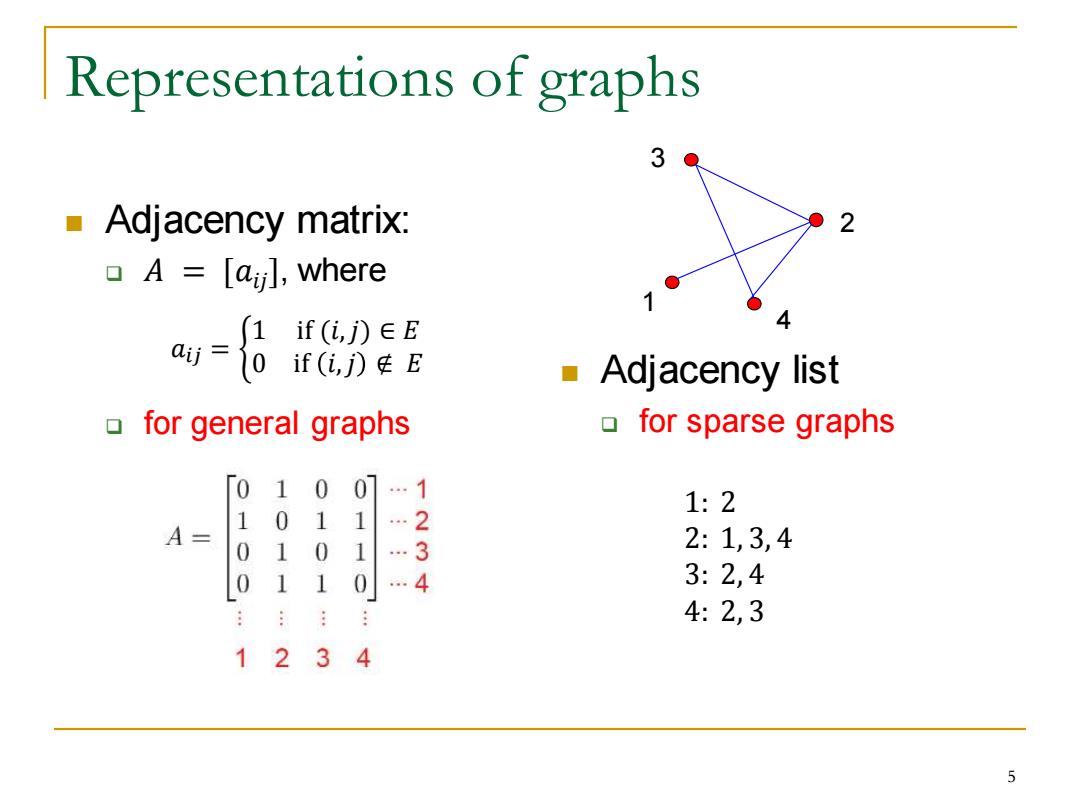
Representations of graphs Adjacency matrix: 2 ▣A=[al,where if (i,j)EE if(i,jE Adjacency list ofor general graphs o for sparse graphs 0 10 07 …1 1 1:2 1 01 A= …2 0 1 0 1 3 2:1,3,4 01 1 0 .…4 3:2,4 4:2,3 12 3 4 5
Representations of graphs ◼ Adjacency matrix: ❑ 𝐴 = [𝑎𝑖𝑗], where ❑ for general graphs ◼ Adjacency list ❑ for sparse graphs 3 1 2 4 𝑎𝑖𝑗 = ቊ 1 if (𝑖,𝑗) ∈ 𝐸 0 if 𝑖,𝑗 ∉ 𝐸 1: 2 2: 1, 3, 4 3: 2, 4 4: 2, 3 5

Size of graph The size of a graph: 01 0 0 …1 1 0 1 A= 0 1 0 11 Adjacency matrix:V2. 0 1 …4 1234 Adjacency list: V+2E for undirected graphs. 1:2 Each undirected edge is counted twice. 2:1,3,4 3:2,4 V+E for directed graphs. 4:2,3 ▣ Each directed edge is counted once. 6
Size of graph ◼ The size of a graph: ❑ Adjacency matrix: 𝑉 2 . ❑ Adjacency list: ◼ |𝑉| + 2|𝐸| for undirected graphs. ❑ Each undirected edge is counted twice. ◼ |𝑉| + |𝐸| for directed graphs. ❑ Each directed edge is counted once. 1: 2 2: 1, 3, 4 3: 2, 4 4: 2, 3 6
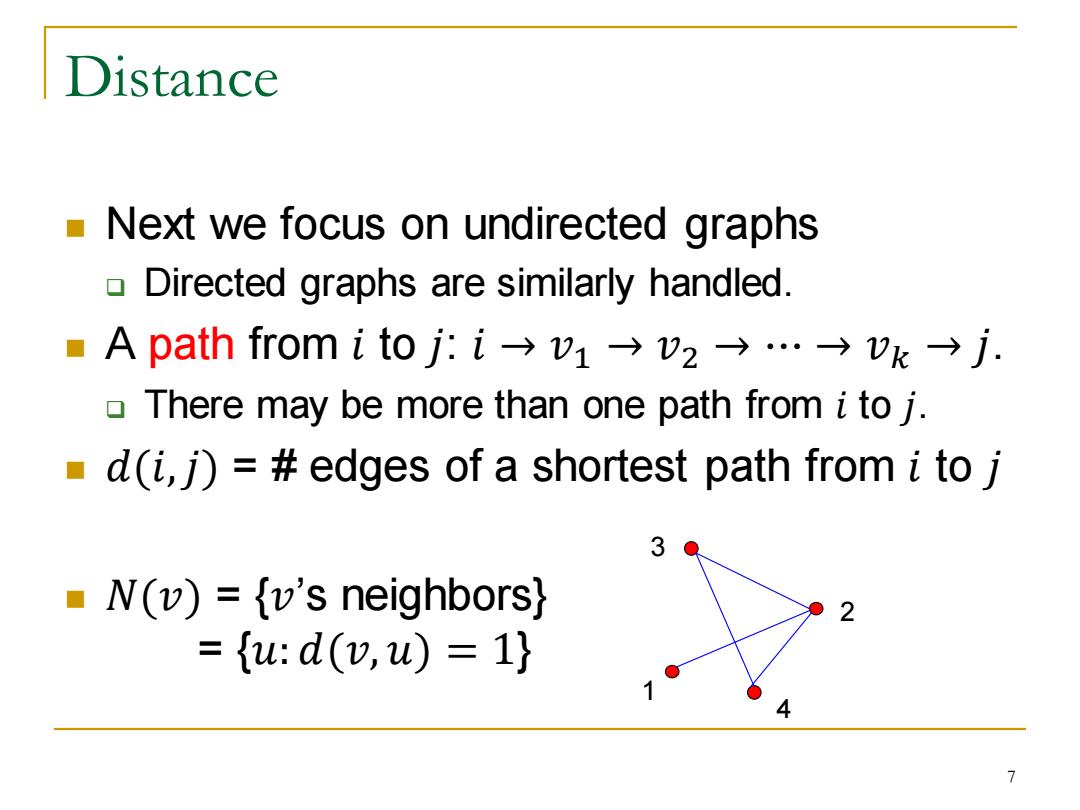
Distance Next we focus on undirected graphs Directed graphs are similarly handled. A path from i to j:i→v1→v2→…→vk→j: There may be more than one path from i to j. d(i,)=#edges of a shortest path from i to j 3 N(v)={v's neighbors) ={u:d(,u)=1}
Distance ◼ Next we focus on undirected graphs ❑ Directed graphs are similarly handled. ◼ A path from 𝑖 to 𝑗: 𝑖 → 𝑣1 → 𝑣2 → ⋯ → 𝑣𝑘 → 𝑗. ❑ There may be more than one path from 𝑖 to 𝑗. ◼ 𝑑(𝑖,𝑗) = # edges of a shortest path from 𝑖 to 𝑗 ◼ 𝑁(𝑣) = {𝑣’s neighbors} = {𝑢: 𝑑(𝑣, 𝑢) = 1} 3 1 2 4 7

A natural question:compute the distance and a shortest path between vertices os→t:st-distance s-all other vertices:Single-Source Shortest Paths 0 all vertices s all other vertices t:All-Pair Shortest paths 8
◼ A natural question: compute the distance and a shortest path between vertices ❑ 𝑠 → 𝑡: 𝑠𝑡-distance ❑ 𝑠 → all other vertices: Single-Source Shortest Paths ❑ all vertices 𝑠 → all other vertices 𝑡: All-Pair Shortest Paths 8
Why shortest paths? Google map for directions Optimal solution of Rubik's cube. Guess what's the number? Erd6s number
Why shortest paths? ◼ Google map for directions ◼ Optimal solution of Rubik’s cube. ❑ Guess what’s the number? ◼ Erdős number 9
st-distance Let's consider the simplest case first:st- distance in an undirected graph. ■How to do it? Even a very inefficient algorithm is ok. S 10
𝑠𝑡-distance ◼ Let’s consider the simplest case first: 𝑠𝑡- distance in an undirected graph. ◼ How to do it? ❑ Even a very inefficient algorithm is ok. s t 10