
CSC3160: Design and Analysis of Algorithms Week 8: Maximum Network Flow Instructor: Shengyu Zhang 1
Instructor: Shengyu Zhang 1
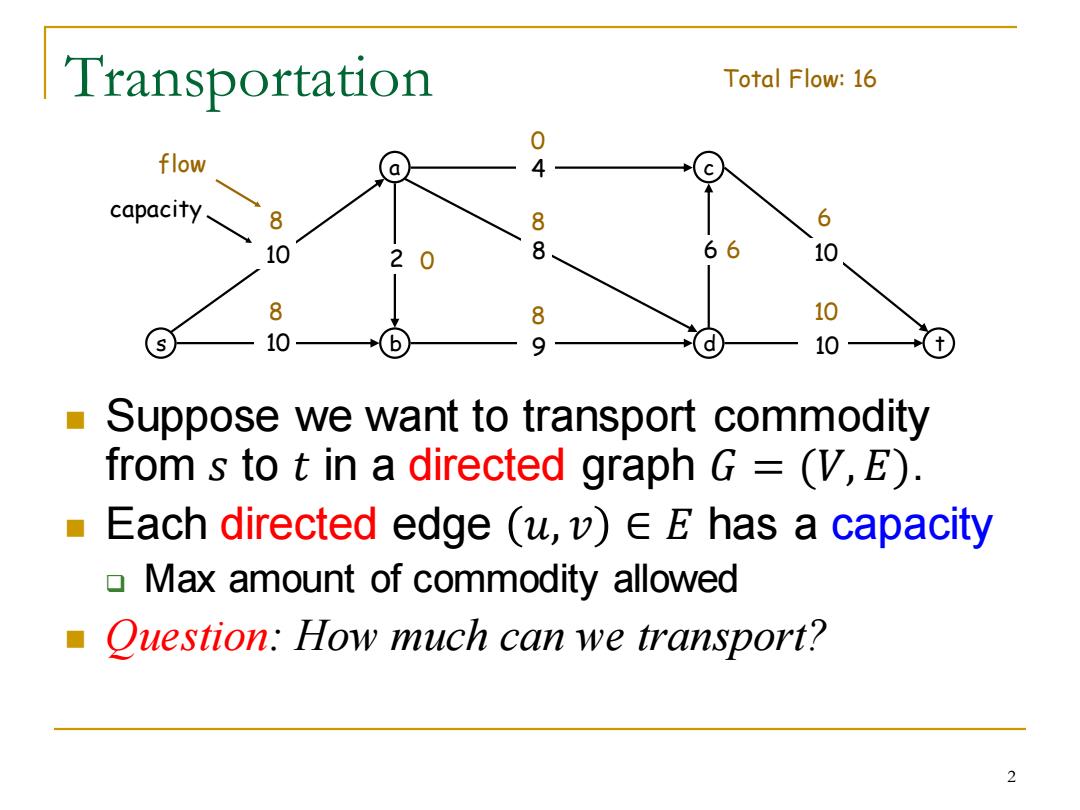
Transportation Total Flow:16 0 flow a 4 capacity 8 8 6 10 2 0 8 66 10 8 8 10 10 9 10 Suppose we want to transport commodity from s to t in a directed graph G=(V,E). Each directed edge (u,v)EE has a capacity Max amount of commodity allowed Question:How much can we transport? 2
Transportation ◼ Suppose we want to transport commodity from 𝑠 to 𝑡 in a directed graph 𝐺 = (𝑉, 𝐸). ◼ Each directed edge 𝑢, 𝑣 ∈ 𝐸 has a capacity ❑ Max amount of commodity allowed ◼ Question: How much can we transport? s a b c 10 d t 10 9 8 4 10 2 6 10 8 0 6 8 8 10 8 0 6 flow Total Flow: 16 capacity 2
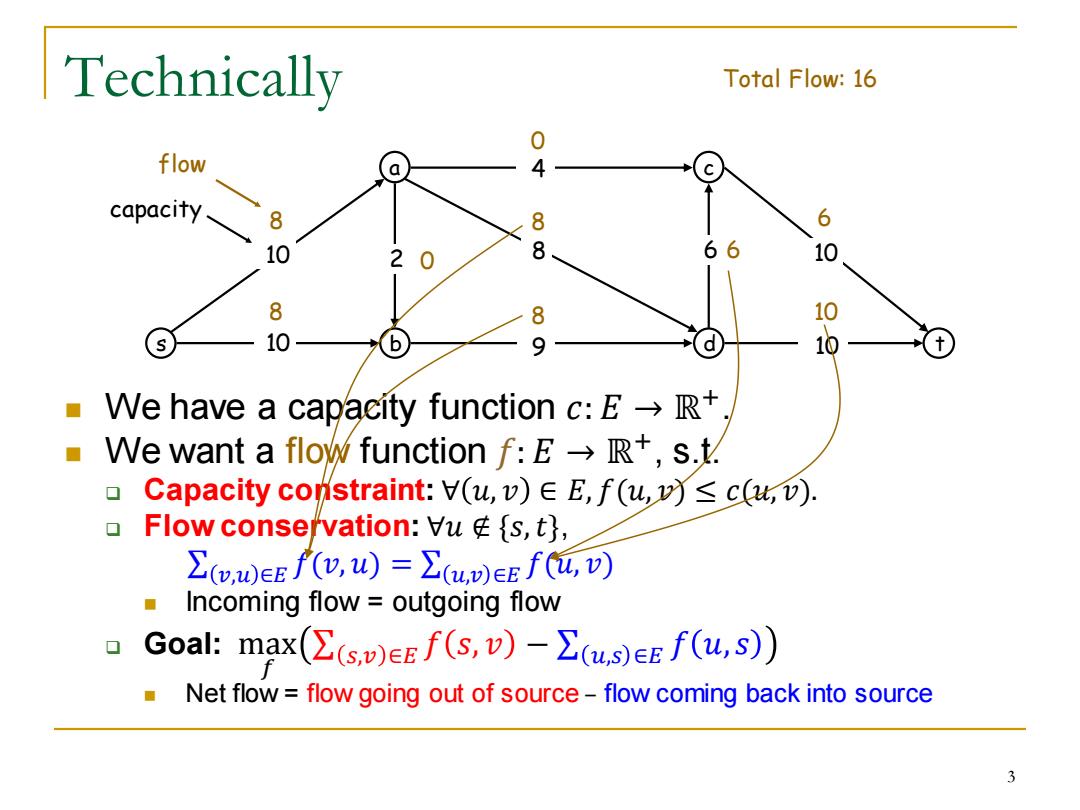
Technically Total Flow:16 0 flow 4 capacity 8 88 6 10 2 6 10 8 8 10 10 9 We have a capacity function c:ER+ We want a flow function f:ER+,s.t. 0 Capacity constraint:V(u,v)EE,f(u,v)<c(u,v). 口 Flow consefvation:Vus,t}, L(o0EEf,W)=∑(uEEf(u可 Incoming flow outgoing flow Goal:max((s)eEf(s,v)-(us)eEf(u,s)) Net flowflow going out of source-flow coming back into source 3
Technically ◼ We have a capacity function 𝑐: 𝐸 → ℝ +. ◼ We want a flow function 𝑓: 𝐸 → ℝ + , s.t. ❑ Capacity constraint: ∀ 𝑢, 𝑣 ∈ 𝐸, 𝑓(𝑢, 𝑣) ≤ 𝑐(𝑢, 𝑣). ❑ Flow conservation: ∀𝑢 ∉ {𝑠,𝑡}, σ 𝑣,𝑢 ∈𝐸 𝑓(𝑣, 𝑢) = σ 𝑢,𝑣 ∈𝐸 𝑓(𝑢, 𝑣) ◼ Incoming flow = outgoing flow ❑ Goal: max 𝑓 σ 𝑠,𝑣 ∈𝐸 𝑓 𝑠, 𝑣 − σ 𝑢,𝑠 ∈𝐸 𝑓 𝑢, 𝑠 ◼ Net flow = flow going out of source – flow coming back into source s a b c 10 d t 10 9 8 4 10 2 6 10 8 0 6 8 8 10 8 0 6 flow Total Flow: 16 capacity 3
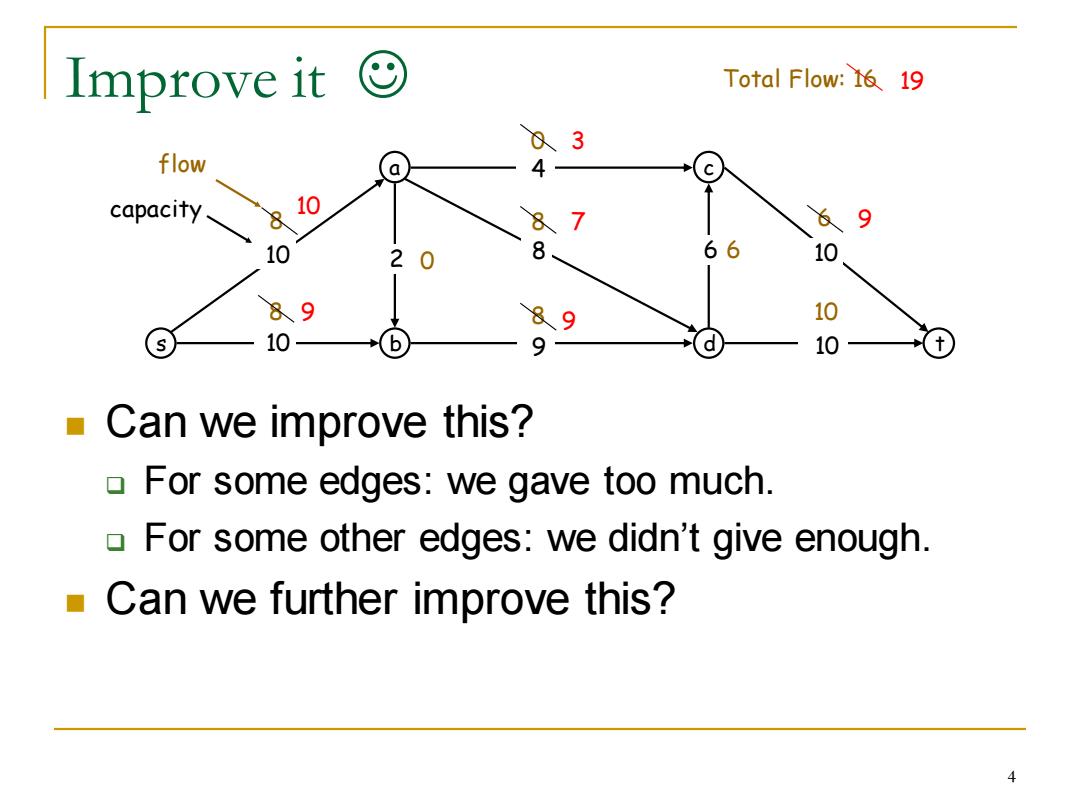
Improve it Total Flow:16 19 03 flow a 4 capacity 10 8 87 9 10 2 0 8 66 10 89 89 10 10 b 9 d 10 Can we improve this? For some edges:we gave too much. For some other edges:we didn't give enough Can we further improve this? 4
Improve it ☺ ◼ Can we improve this? ❑ For some edges: we gave too much. ❑ For some other edges: we didn’t give enough. ◼ Can we further improve this? s a b c 10 d t 10 9 8 4 10 2 6 10 8 0 6 8 8 10 8 0 6 flow Total Flow: 16 capacity 7 9 3 10 9 9 19 4

Network Flow Can you give a good algorithm? Methodology 5:Approach to the optimum by a sequence of improvements. 5
Network Flow ◼ Can you give a good algorithm? ◼ Methodology 5: Approach to the optimum by a sequence of improvements. 5
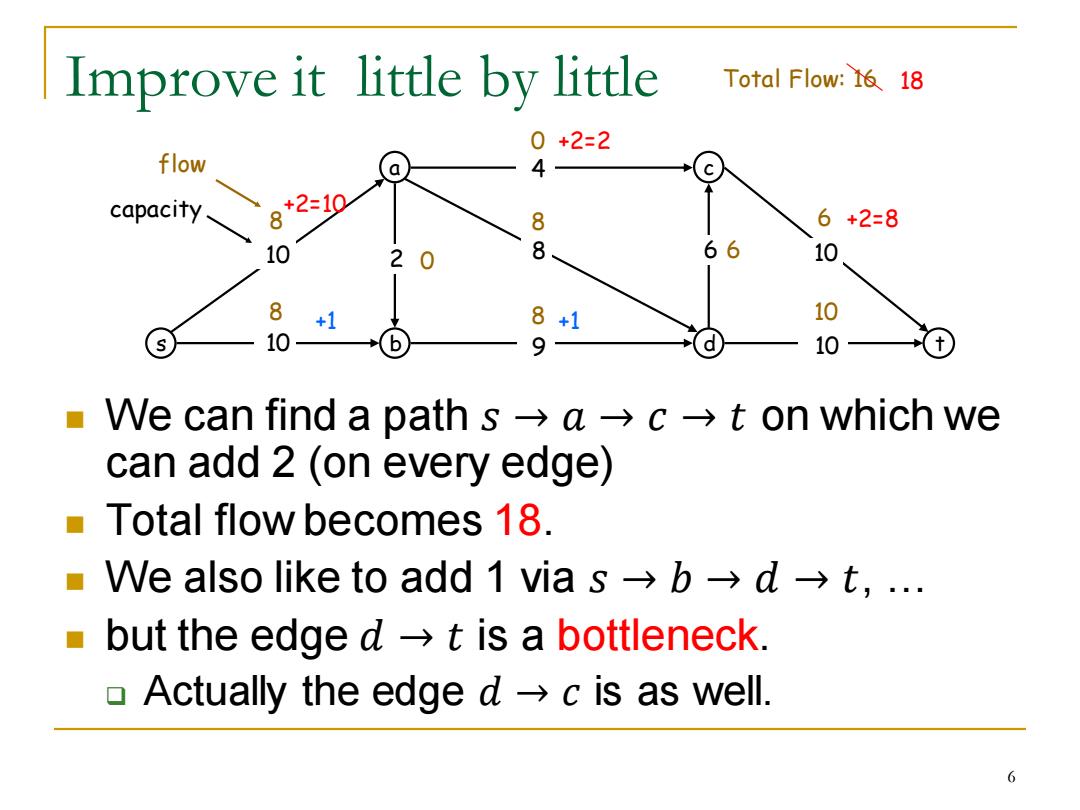
Improve it little by little Total Flow:16 18 0+2=2 flow capacity +2=10 8 8 6+2=8 10 2 8 66 10 8 +1 8+1 10 10 9 10 Ve can find a path s→a→c→t on which we can add 2 (on every edge) Total flow becomes 18. ■ Ve also like to add1vias→b→d→t,.. but the edge dt is a bottleneck. ▣Actually the edge d→c is as well. 6
Improve it little by little ◼ We can find a path 𝑠 → 𝑎 → 𝑐 → 𝑡 on which we can add 2 (on every edge) ◼ Total flow becomes 18. ◼ We also like to add 1 via 𝑠 → 𝑏 → 𝑑 → 𝑡, … ◼ but the edge 𝑑 → 𝑡 is a bottleneck. ❑ Actually the edge 𝑑 → 𝑐 is as well. s a b c 10 d t 10 9 8 4 10 2 6 10 8 0 6 8 8 10 8 0 6 flow Total Flow: 16 capacity +2=8 +2=2 +2=10 +1 +1 18 6
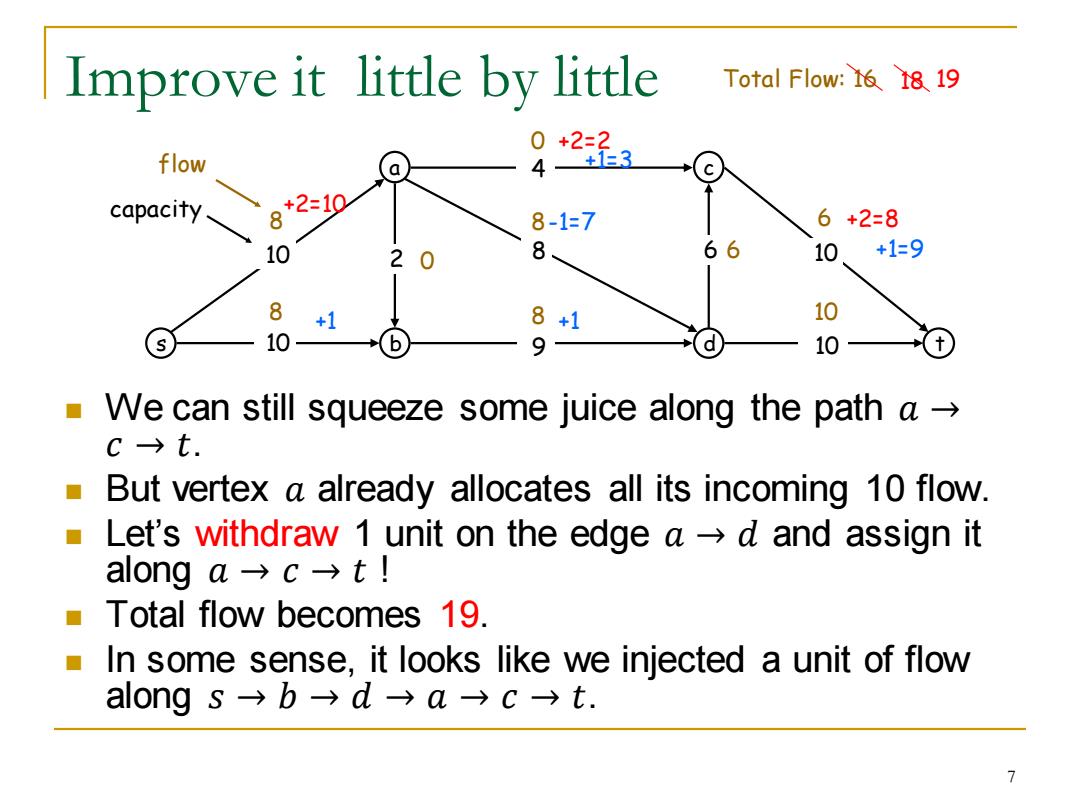
Improve it little by little Total Flow:16 18 19 0+2=2 flow +E capacity +2=10 8 8-1=7 6+2=8 10 8 66 10 +1=9 8 +1 8+1 10 10 9 10 We can still squeeze some juice along the path a C→t. But vertex a already allocates all its incoming 10 flow. Let's withdraw 1 unit on the edge a>d and assign it along a→c→tI Total flow becomes 19. ■ In some sense,it looks like we injected a unit of flow along s→b→d→a→c→t. 7
Improve it little by little ◼ We can still squeeze some juice along the path 𝑎 → 𝑐 → 𝑡. ◼ But vertex 𝑎 already allocates all its incoming 10 flow. ◼ Let’s withdraw 1 unit on the edge 𝑎 → 𝑑 and assign it along 𝑎 → 𝑐 → 𝑡 ! ◼ Total flow becomes 19. ◼ In some sense, it looks like we injected a unit of flow along 𝑠 → 𝑏 → 𝑑 → 𝑎 → 𝑐 → 𝑡. s a b c 10 d t 10 9 8 4 10 2 6 10 8 0 6 8 8 10 8 0 6 flow Total Flow: 16 capacity +2=8 +2=2 +2=10 +1 +1 -1=7 +1=3 +1=9 18 19 7
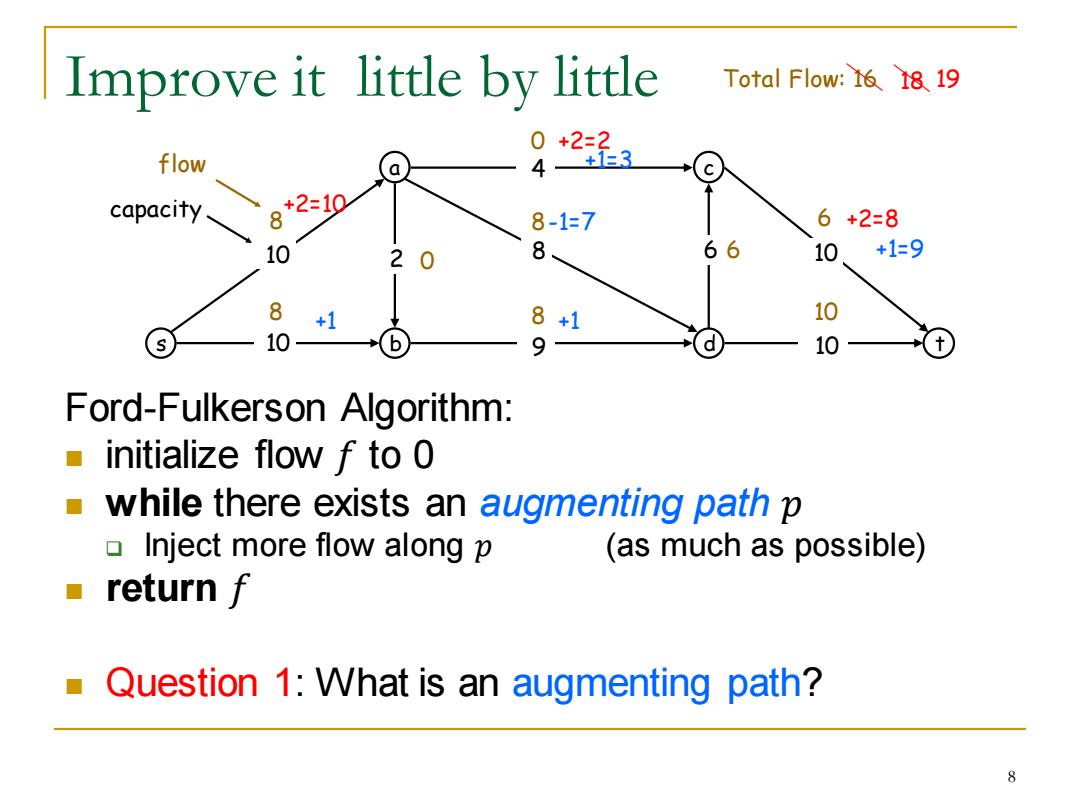
Improve it little by little Total Flow:16 18 19 flow 9+2 capacity +2=10 8 8-1=7 6+2=8 10 2 8 66 10 +1=9 8 +1 8+1 10 10 9 d 10 Ford-Fulkerson Algorithm: a initialize flow f to 0 while there exists an augmenting path p Inject more flow along p (as much as possible) return f Question 1:What is an augmenting path? 8
Improve it little by little Ford-Fulkerson Algorithm: ◼ initialize flow 𝑓 to 0 ◼ while there exists an augmenting path 𝑝 ❑ Inject more flow along 𝑝 (as much as possible) ◼ return 𝑓 ◼ Question 1: What is an augmenting path? s a b c 10 d t 10 9 8 4 10 2 6 10 8 0 6 8 8 10 8 0 6 flow Total Flow: 16 capacity +2=8 +2=2 +2=10 +1 +1 -1=7 +1=3 +1=9 18 19 8
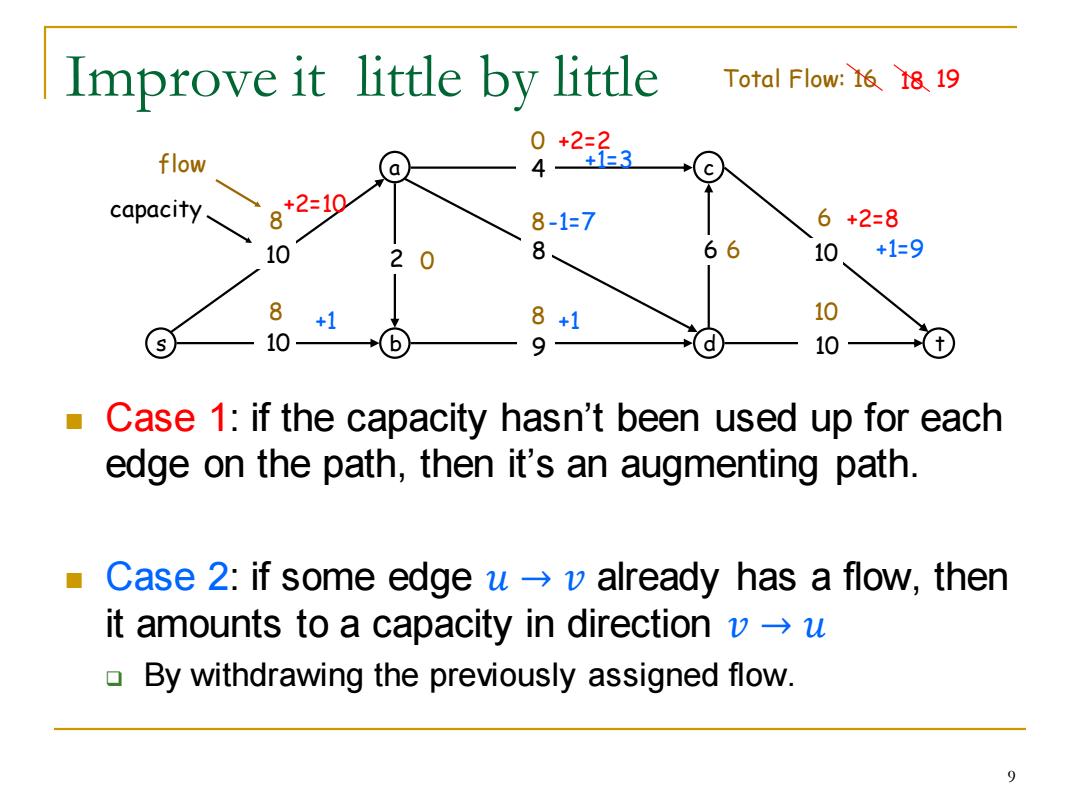
Improve it little by little Total Flow:16 18 19 0+2=2 flow 0 + capacity +2=10 8 8-1=7 6+2=8 10 2 8 66 10 +1=9 8 8+1 10 10 9 10 Case 1:if the capacity hasn't been used up for each edge on the path,then it's an augmenting path. Case 2:if some edge uv already has a flow,then it amounts to a capacity in direction vu By withdrawing the previously assigned flow. 9
Improve it little by little ◼ Case 1: if the capacity hasn’t been used up for each edge on the path, then it’s an augmenting path. ◼ Case 2: if some edge 𝑢 → 𝑣 already has a flow, then it amounts to a capacity in direction 𝑣 → 𝑢 ❑ By withdrawing the previously assigned flow. s a b c 10 d t 10 9 8 4 10 2 6 10 8 0 6 8 8 10 8 0 6 flow Total Flow: 16 capacity +2=8 +2=2 +2=10 +1 +1 -1=7 +1=3 +1=9 18 19 9

Improve it little by little Total Flow:16 18 19 flow 0 +2 4 capacity +2=10 8 8-1=7 6+2=8 10 2 0 8 66 10 +1=9 8 +1 8+1 10 10 9 d 10 Question 2:How to find an augmenting path? By residual networks. 10
Improve it little by little ◼ Question 2: How to find an augmenting path? ◼ By residual networks. s a b c 10 d t 10 9 8 4 10 2 6 10 8 0 6 8 8 10 8 0 6 flow Total Flow: 16 capacity +2=8 +2=2 +2=10 +1 +1 -1=7 +1=3 +1=9 18 19 10