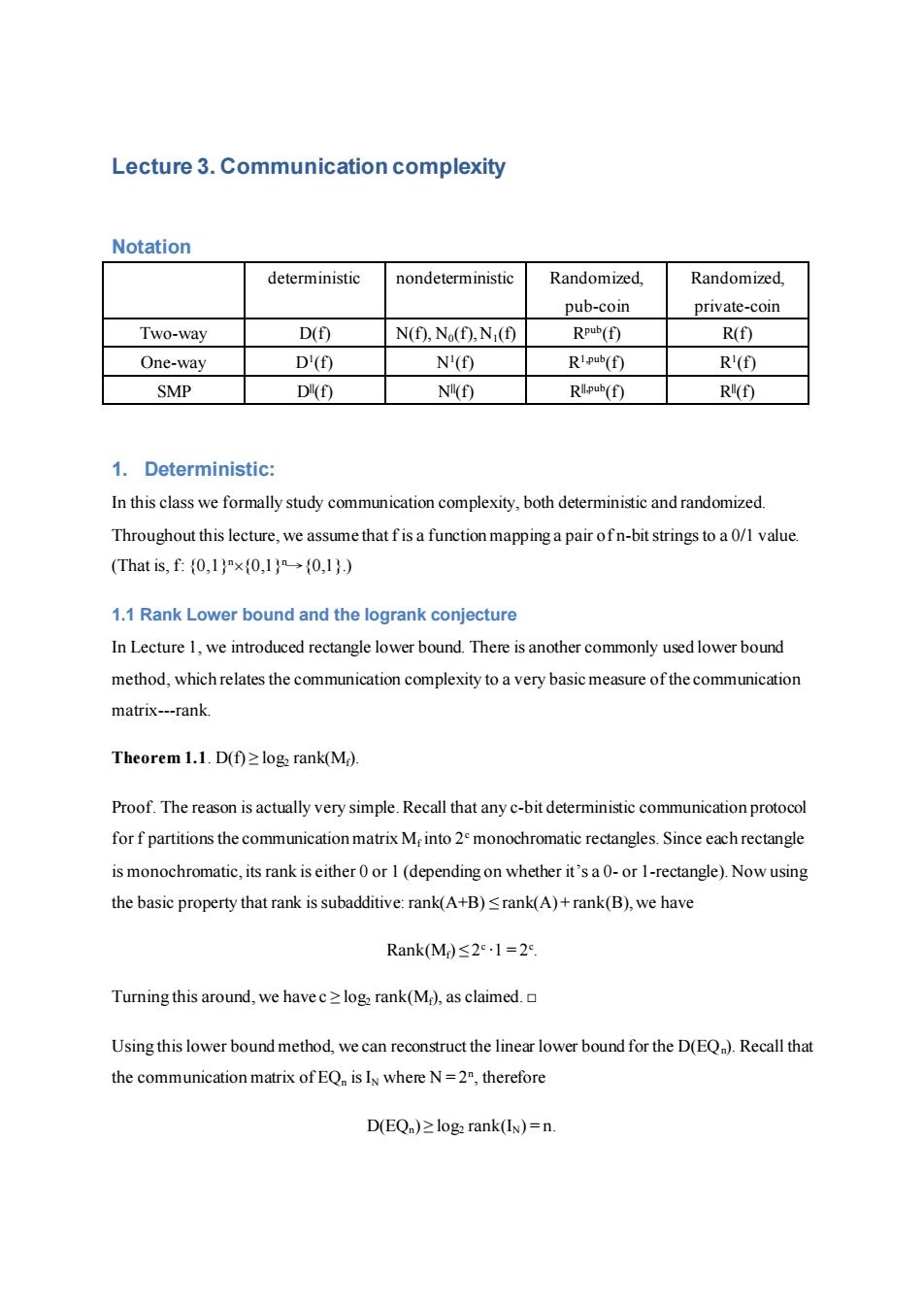
Lecture 3.Communication complexity Notation deterministic nondeterministic Randomized. Randomized, pub-coin private-coin Two-way D() N(f),No(f),N (f) Rpub(f) R(f) One-way D'(f) N'() R1pub(f) R'( SMP Di(f) NI(f) RIlpub(f) R() 1.Deterministic: In this class we formally study communication complexity,both deterministic and randomized. Throughout this lecture,we assume that fis a function mapping a pair of n-bit strings to a 0/1 value. (That is,f:(0,1)"x(0,1)(0,1).) 1.1 Rank Lower bound and the logrank conjecture In Lecture 1,we introduced rectangle lower bound.There is another commonly used lower bound method,which relates the communication complexity to a very basic measure of the communication matrix---rank Theorem 1.1.D(f)z logz rank(M). Proof.The reason is actually very simple.Recall that any c-bit deterministic communication protocol for f partitions the communication matrix M into 2 monochromatic rectangles.Since each rectangle is monochromatic,its rank is either 0 or 1 (depending on whether it's a 0-or 1-rectangle).Now using the basic property that rank is subadditive:rank(A+B)log.rank(M),as claimed. Using this lower bound method,we can reconstruct the linear lower bound for the D(EQ).Recall that the communication matrix of EQ is In where N=2,therefore D(EQ)>log2 rank(IN)=n
Lecture 3. Communication complexity Notation deterministic nondeterministic Randomized, pub-coin Randomized, private-coin Two-way D(f) N(f), N0(f), N1(f) Rpub(f) R(f) One-way D1 (f) N1 (f) R1,pub(f) R1 (f) SMP D||(f) N||(f) R||,pub(f) R||(f) 1. Deterministic: In this class we formally study communication complexity, both deterministic and randomized. Throughout this lecture, we assume that f is a function mapping a pair of n-bit strings to a 0/1 value. (That is, f: {0,1}n{0,1}n→{0,1}.) 1.1 Rank Lower bound and the logrank conjecture In Lecture 1, we introduced rectangle lower bound. There is another commonly used lower bound method, which relates the communication complexity to a very basic measure of the communication matrix---rank. Theorem 1.1. D(f) ≥ log2 rank(Mf). Proof. The reason is actually very simple. Recall that any c-bit deterministic communication protocol for f partitions the communication matrix Mf into 2c monochromatic rectangles. Since each rectangle is monochromatic, its rank is either 0 or 1 (depending on whether it’s a 0- or 1-rectangle). Now using the basic property that rank is subadditive: rank(A+B) ≤ rank(A) + rank(B), we have Rank(Mf) ≤ 2 c ∙1 = 2c . Turning this around, we have c ≥ log2 rank(Mf), as claimed. □ Using this lower bound method, we can reconstruct the linear lower bound for the D(EQn). Recall that the communication matrix of EQn is IN where N = 2n , therefore D(EQn) ≥ log2 rank(IN) = n

Exercise.Define the "Greater Than"function as GT(x,y)=1 if x>y and 0 otherwise,where we view x and y as binary representation of two integers in [0,2-1].Show that D(GT)>n. Whenever you have a lower bound method,a natural question is how tight the method is.It would be great if it's tight up to a constant,but that's usually too good to be true.A moderate hope is that the lower bound is "polynomially tight",namely tight after being raised to a certain constant power.In the case of communication complexity,it's the following famous"Logrank conjecture"[LS88]. Conjecture (Logrank):Is there a constant c,such that for all f,D(f)=(loge rank(M))? Despite many efforts,it's still wide open.The largest separation is D(f)(log2 rank(M))for c= log 6=1.63...,while the best upper bound is still the trivial D(f)<rank(M). Exercise.Prove that D(f)<rank(M). 2.Randomized: The randomized communication complexity actually depends on the required error probability,which we will use the subscript to specify.For example,R (f)is the 8-error private-coin randomized communication complexity.When we don't specify the error probability,it's 1/3 by convention;that is,R(f)=R(f).Like in randomized algorithms,the error probability can be decreased froma constant to an arbitrary &by repeating the protocol O(log 1/a)times.(Details will be given in tutorial.) 2.1 Power of public randomness---Newman's theorem. Recall that in the first lecture we showed that RPub(EQ)=O(1),and the protocol crucially uses the assumption that Alice and Bob share many random bits.However,the next theorem tells that even if they don't share any random bits,they can still compute the function efficiently,with a loss of mere O(logn).And this is true for all functions! Theorem 2.1.R+s(f)<R Pub(f)+O(log(n/5)). Proof.We will actually show a stronger result,that any public-coin protocol P can be made to a new protocol P'which uses only s-O(log(n/))public random bits,with the error probability being increased by only 8.If this is true,then to get a private-coin protocol,Alice can simply first tosss random bits and then send them to Bob,who then share these many random bits with Alice.They then run the public-coin protocol P
Exercise. Define the “Greater Than” function as GTn(x,y) = 1 if x > y and 0 otherwise, where we view x and y as binary representation of two integers in [0, 2n -1]. Show that D(GTn) ≥ n. Whenever you have a lower bound method, a natural question is how tight the method is. It would be great if it’s tight up to a constant, but that’s usually too good to be true. A moderate hope is that the lower bound is “polynomially tight”, namely tight after being raised to a certain constant power. In the case of communication complexity, it’s the following famous “Logrank conjecture” [LS88]. Conjecture (Logrank): Is there a constant c, such that for all f, D(f) = (log2 rank(Mf))c ? Despite many efforts, it’s still wide open. The largest separation is D(f) ≥ (log2 rank(Mf))c for c = log36 = 1.63…, while the best upper bound is still the trivial D(f) ≤ rank(Mf). Exercise. Prove that D(f) ≤ rank(Mf). 2. Randomized: The randomized communication complexity actually depends on the required error probability, which we will use the subscript to specify. For example, Rε(f) is the ε-error private-coin randomized communication complexity. When we don’t specify the error probability, it’s 1/3 by convention; that is, R(f) = R1/3(f). Like in randomized algorithms, the error probability can be decreased from a constant to an arbitrary ε by repeating the protocol O(log 1/ε) times. (Details will be given in tutorial.) 2.1 Power of public randomness---Newman’s theorem. Recall that in the first lecture we showed that Rpub(EQn) = O(1), and the protocol crucially uses the assumption that Alice and Bob share many random bits. However, the next theorem tells that even if they don’t share any random bits, they can still compute the function efficiently, with a loss of mere O(log n). And this is true for all functions! Theorem 2.1. Rε+δ(f) ≤ Rε pub(f) + O(log(n/δ)). Proof. We will actually show a stronger result, that any public-coin protocol P can be made to a new protocol P’ which uses only s=O(log(n/δ)) public random bits, with the error probability being increased by only δ. If this is true, then to get a private-coin protocol, Alice can simply first toss s random bits and then send them to Bob, who then share these many random bits with Alice. They then run the public-coin protocol P’

So how to design P'from P?Suppose P uses a lot of public randomness.Say P samples from a huge set of random strings R.We will show that there exist a small size t=O(n/82)))subset (r1,...,r)of R s.t.the following protocol P'has error probability at most that of P plus 8. P':Alice and Bob sample i from {1,...,t),and then run P on the random stringri. How to show the existence of such (r1,...,r)?Let's try to find them by random samplings.Namely, let's imagine to run Pttimes,which samplestri's.Use them as (r,...,).Let's see that with a good probability,the resulting set (r,...,r)satisfies the above condition. Consider the error probability for a fixed input(x,y):Pr[error]=(W(x,y,r)+...+W(x,y,n))/t,where W(x,y,ri)=1 if P on(x,y,ri)gives wrong answer,and 0 otherwise.Note that E i[W(x.y,r)]]5]<exp(-82te/2e2)=exp(-Q(82t)). So for each fixed(x,y),if we getri's in the above way,and run P,then with very high probability of the choice of r's,the error probability of P'on(x,y)is at most 8+8.We are almost done,except that p' needs to be comrect on all inputs(x,y).So let's see the probability that the ri's is"bad"for some(x,y), where“bad”means that it results in the error probability more than s+δ: Pr,.l,,t[日(x,y),s.tri's is"bad”for(x,y】≤22nexp(-2(8t)<1 ift=2(n/82).口 In the above proof we use random sampling to show existence ofr,'s.This is a typical application of the probabilistic method.For a comprehensive introduction to this powerful method,see the classic textbook [AS08]. This theorem immediately implies the following upper bound. Theorem 2.2.R(EQ)=O(logn). Exercise.Show that actually it's enough to use a one-way protocol:R'(EQ)=O(log n).(hint:both the public-coin protocol for EO,and the above simulation technique in the above proofare one-way.)
So how to design P’ from P? Suppose P uses a lot of public randomness. Say P samples from a huge set of random strings R. We will show that there exist a small ( size t = O(n/δ 2 )) ) subset {r1, …, rt} of R s.t. the following protocol P’ has error probability at most that of P plus δ. P’: Alice and Bob sample i from {1, …, t}, and then run P on the random string ri . How to show the existence of such {r1, …, rt}? Let’s try to find them by random samplings. Namely, let’s imagine to run P t times, which samples t ri’s. Use them as {r1, …, rt}. Let’s see that with a good probability, the resulting set {r1, …, rt} satisfies the above condition. Consider the error probability for a fixed input (x,y): Pr[error] = (W(x,y,r1) + … + W(x,y,rt))/t, where W(x,y,ri) = 1 if P on (x,y,ri) gives wrong answer, and 0 otherwise. Note that Er_i[W(x,y,rt)] ≤ ε by the correctness of P. Recall Chernoff’s bound: Pr[|(X1+…+Xt)/t – μ| > δ] δ] < exp(-δ 2 tε/2ε 2 ) = exp(-Ω(δ 2 t)). So for each fixed (x,y), if we get ri’s in the above way, and run P’, then with very high probability of the choice of ri’s, the error probability of P’ on (x,y) is at most ε+δ. We are almost done, except that P’ needs to be correct on all inputs (x,y). So let’s see the probability that the ri’s is “bad” for some (x,y), where “bad” means that it results in the error probability more than ε+δ: Prr_1, …, r_t [(x,y), s.t. ri’s is “bad” for (x,y)] ≤ 2 2n exp(-Ω(δ 2 t)) < 1 if t = Ω(n/δ 2 ). □ In the above proof we use random sampling to show existence of ri’s. This is a typical application of the probabilistic method. For a comprehensive introduction to this powerful method, see the classic textbook [AS08]. This theorem immediately implies the following upper bound. Theorem 2.2. R(EQn) = O(log n). Exercise. Show that actually it’s enough to use a one-way protocol: R1 (EQn) = O(log n). (hint: both the public-coin protocol for EQn and the above simulation technique in the above proof are one-way.)

Let's mention(without proof)the following relation between R(f)and D(f). Theorem 2.3.R(f)=Q(log D(f)). This implies that R(EQ)=(logn).Therefore,the additive log(n)term in Theorem 2.1 is necessary 2.2 Distributional complexity We have seen that randomness can help to significantly reduce the communication complexity for certain functions like Equality.Howabout other functions,say,Inner Product(IP),whose definition was given in Lecture 1: Inner Product (IP):To compute (xy)=xiy1+...+xnyn mod 2,where x.yE(0,1) After trying efficient protocols for a while(and failing),one wonders whether R(IP)is actually large This raises a natural question:How to prove lower bound for randomized communication complexity? While we know rectangle and rank as two lower bound methods for deterministic communication complexity,it seems much harder to argue about an arbitrary randomized protocol.Nonetheless,there is a close connection between the deterministic and randomized communication complexity First,suppose that a randomized protocol P computes a function f with error probability at most 8. Now consider to relax the worst-case error requirement:Instead ofrequiring P to have small error probability for any input(x,y),we now first draw(x,y)from a distribution p over the input set (0,1)"x(0,1)",and merely require that P has small error probability on average input(x,y)--p.(Here (x,y)-p means to draw(x,y)from distribution p.)Note that this is a weaker requirement,since P may be always wrong on some input(x,y)yet still satisfies the requirement,as long as p(x,y)is very small. To be more precise,for any protocol P and any distribution p,the p-distributional erroris E)p[error probability of P on (x,y)]. Define the p-distributional communication complexity to be the communication cost for the best protocol that has p-distributional error at most &We didn't specify whether the"best protocol"is deterministic or randomized,because it doesn't matter---the optimum is always achieved by a deterministic protocol.(The error for any randomized one can be viewed as the convex combination of the errors for some deterministic ones.)We denote by De(f)the p-distributional communication complexity of f.Clearly,R(f)>D(f).However,the following theorem shows that this seemingly weaker condition doesn't lose anything,as long as we pick the right distribution p
Let’s mention (without proof) the following relation between R(f) and D(f). Theorem 2.3. R(f) = Ω(log D(f)). This implies that R(EQn) = Ω(log n). Therefore, the additive log(n) term in Theorem 2.1 is necessary. 2.2 Distributional complexity We have seen that randomness can help to significantly reduce the communication complexity for certain functions like Equality. How about other functions, say, Inner Product (IPn), whose definition was given in Lecture 1: Inner Product (IPn): To compute x,y= x1y1 + … + xnyn mod 2, where x,y{0,1}n . After trying efficient protocols for a while (and failing), one wonders whether R(IPn) is actually large. This raises a natural question: How to prove lower bound for randomized communication complexity? While we know rectangle and rank as two lower bound methods for deterministic communication complexity, it seems much harder to argue about an arbitrary randomized protocol. Nonetheless, there is a close connection between the deterministic and randomized communication complexity. First, suppose that a randomized protocol P computes a function f with error probability at most ε. Now consider to relax the worst-case error requirement: Instead of requiring P to have small error probability for any input (x,y), we now first draw (x,y) from a distribution p over the input set {0,1}n{0,1}n , and merely require that P has small error probability on average input (x,y)←p. (Here (x,y)←p means to draw (x,y) from distribution p.) Note that this is a weaker requirement, since P may be always wrong on some input (x,y) yet still satisfies the requirement, as long as p(x,y) is very small. To be more precise, for any protocol P and any distribution p, the p-distributional erroris E(x,y)←p[error probability of P on (x,y)]. Define the p-distributional communication complexity to be the communication cost for the best protocol that has p-distributional error at most ε. We didn’t specify whether the “best protocol” is deterministic or randomized, because it doesn’t matter---the optimum is always achieved by a deterministic protocol. (The error for any randomized one can be viewed as the convex combination of the errors for some deterministic ones.) We denote by 𝐷𝜀 𝑝 (f) the p-distributional communication complexity of f. Clearly, Rε(f) ≥𝐷𝜀 𝑝 (f). However, the following theorem shows that this seemingly weaker condition doesn’t lose anything, as long as we pick the right distribution p

Theorem 2.4.R(f)=maxp D2(f). We will not prove this theorem;it follows from the minimax theorems in game theory.(Terminology: Yao first introduced the minimax theorem with applications in theoretical computer science,so this type of theorems is sometimes called Yao'sprinciple in the literature.)Thus,to showlower bound for R (f),it's enough to pick one distribution p on inputs,and then show that any deterministic protocol of small communication cost has a large error probability.Note that this changes the task of handling randomized protocols to arguing for deterministic protocols. Let's now show the discrepancy bound.For a function f,a distribution p and a rectangle R,define the discrepancy as discp(R,f)=|Pr)-p[f(x,y)=0 and (x,y)ER]-Pr()-p[f(x.y)=1 and (x,y)ER]l, and define disc (f)=maxg disc (R,f).Intuitively,if disc (f)is small,then all rectangles are very balanced in zeros and ones.Thus a protocol,when reaching at the rectangle and forced to output something,has inevitably a large error probability.The following theorem makes this rigorous. Theorem2.5.D2-(f)zlog(2e/disc;(f)). Proof.For a rectangle R,define error(R)to be the minimum error for any protocol to give a fixed 0/1 value as the answer to all the inputs in R.From the definition of discrepancy,it's not hard to see that error(R)=(1-disc(R,f)/p(R))/2.For any c-bit deterministic protocol with distributional error at most 1/2-g,calculate its distributional error from the rectangles: distributional error=ER p(R)error(R)=ER(p(R)-discp(R,f))/21/2-discp(f)2c-1. Thus 1/2-discp()2e-l≤l/2-e,and thus c≥log(2e/discp(①).口 Let's now use it to show that IP is hard even for randomized protocols. Theorem 2.6.RPub(IP)=(n). Proof.We will actually show that D(IP)n-log(1/),where p is the uniform distribution: p(x,y)=1/22.Change f to range:g(x,y)=1 if f(x.y)=0,and g(x,y)=-1 if f(x,y)=1.Then for any rectangle R=SxT, discp(R,f)=|∑xesyeT g(x,y)川/22n=(1s.Glr〉/22n
Theorem 2.4. Rε(f) = maxp 𝐷𝜀 𝑝 (f). We will not prove this theorem; it follows from the minimax theorems in game theory. (Terminology: Yao first introduced the minimax theorem with applications in theoretical computer science, so this type of theorems is sometimes called Yao’s principle in the literature.) Thus, to show lower bound for Rε(f), it’s enough to pick one distribution p on inputs, and then show that any deterministic protocol of small communication cost has a large error probability. Note that this changes the task of handling randomized protocols to arguing for deterministic protocols. Let’s now show the discrepancy bound. For a function f, a distribution p and a rectangle R, define the discrepancy as discp(R,f) = | Pr(x,y)←p[f(x,y) = 0 and (x,y)R] - Pr(x,y)←p[f(x,y) = 1 and (x,y)R] |, and define discp(f) = maxR discp(R,f). Intuitively, if discp(f) is small, then all rectangles are very balanced in zeros and ones. Thus a protocol, when reaching at the rectangle and forced to output something, has inevitably a large error probability. The following theorem makes this rigorous. Theorem 2.5. 𝐷1/2−𝜀 𝑝 (f) ≥ log2(2ε/discp(f)). Proof. For a rectangle R, define error(R) to be the minimum error for any protocol to give a fixed 0/1 value as the answer to all the inputs in R. From the definition of discrepancy, it’s not hard to see that error(R) = (1 - disc(R,f) / p(R))/2. For any c-bit deterministic protocol with distributional error at most 1/2-ε, calculate its distributional error from the rectangles: distributional error = ∑R p(R) error(R) = ∑R (p(R) - discp(R,f)) / 2 ≥ 1/2 – discp(f) 2c-1 . Thus 1/2 – discp(f) 2c-1 ≤ 1/2-ε, and thus c ≥ log2(2ε/discp(f)). □ Let’s now use it to show that IPn is hard even for randomized protocols. Theorem 2.6. Rpub(IPn) = Ω(n). Proof. We will actually show that 𝐷1/2−𝜀 𝑝 (IPn) ≥ n/2 – log(1/ε), where p is the uniform distribution: p(x,y) = 1/22n . Change f to ±range: g(x,y) = 1 if f(x,y) = 0, and g(x,y) = -1 if f(x,y) = 1. Then for any rectangle R = ST, discp(R,f) = | ∑xS,yT g(x,y) | / 22n = 1S, G1T / 22n

where G=[g(x,y)]and Is is the (column)indicator vector forS:Is(x)=1 if xeS,and0 otherwise.G is actually the Hadamard matrix,whose maximum eigenvaluellGll2 is well-known to be 22.(To see this,note that GH where Hwith maximumeigenvalueand tenor product has the property that AB2=All2Bl2.)Also recall the fact 1sllalGlVISIITI2m/2 1 discp(R,f)≤ 22n 22n≤2 Plugging this into Theorem 2.5 gives the claimed bound. For specific functions,there is another very important example,Disjn Disjointness (Disjn):To decide whether 3i s.t.xi=yi=I for x,ye(0,1). Let's mention without proof the following important result. Theorem.R(Disjn)=(n). This can be proved by distributional complexity as well,but the technical details are a bit too heavy for this class.One can see [Raz90]for details.There is another beautiful proof in [BYJK+03],which belongs to the general category of using information theoretic argument to prove lower bounds in computer science---a topic which I'd like to present if we have time later in the course. References [AS08]Noga Alon,Joel Spencer.The Probabilistic Method,3rd edition,John Wiley Sons,2008. [BYJK+03]Ziv Bar-Yossef,,I T.S.Jayram,Ravi Kumar,and D.Sivakumar.An information statistics approach to data stream and communication complexity.Journal ofComputer and System Sciences 68,pp.702-732,2004 [LS88]L Lovasz and Michael Saks.Lattices,Mobius functions,and communication complexity. Proceedings ofthe 29h Foundations ofComputer Science,pp.81-90,1988. [Raz90]Alexander Razborov.On the Distributional Complexity of Disjointness,Theoretical Computer Science 106(2),pp.385-390,1992
where G = [g(x,y)] and 1S is the (column) indicator vector for S: 1S(x) = 1 if xS, and 0 otherwise. G is actually the Hadamard matrix, whose maximum eigenvalue ||G||2 is well-known to be 2n/2 . (To see this, note that G = H2 n , where H2 = [ 1 1 1 −1 ] with maximum eigenvalue 2 1/2, and tensor product has the property that ||AB||2 = ||A||2 ||B||2.) Also recall the fact disc𝑝 (𝑅,𝑓) ≤ ‖1𝑆 ‖2 ‖𝐺‖2 ‖1𝑇 ‖2 2 2𝑛 = √|𝑆||𝑇|2 𝑛/2 2 2𝑛 ≤ 1 2 𝑛/2 . Plugging this into Theorem 2.5 gives the claimed bound.□ For specific functions, there is another very important example, Disjn. Disjointness (Disjn): To decide whether i s.t. xi = yi = 1 for x,y{0,1}n . Let’s mention without proof the following important result. Theorem. R(Disjn) = Ω(n). This can be proved by distributional complexity as well, but the technical details are a bit too heavy for this class. One can see [Raz90] for details. There is another beautiful proof in [BYJK+03], which belongs to the general category of using information theoretic argument to prove lower bounds in computer science---a topic which I’d like to present if we have time later in the course. References [AS08] Noga Alon, Joel Spencer.The Probabilistic Method, 3rd edition, John Wiley & Sons, 2008. [BYJK+03] Ziv Bar-Yossef,,1 T.S. Jayram, Ravi Kumar, and D. Sivakumar. An information statistics approach to data stream and communication complexity. Journal of Computer and System Sciences 68, pp. 702–732, 2004. [LS88] L Lovasz and Michael Saks. Lattices, Mobius functions, and communication complexity. Proceedings of the 29th Foundations of Computer Science, pp. 81-90, 1988. [Raz90] Alexander Razborov.On the Distributional Complexity of Disjointness, Theoretical Computer Science 106(2), pp. 385-390, 1992