
CSCI 3160 Design and Analysis of Algorithms Tutorial 2 Chengyu Lin ● ●
CSCI 3160 Design and Analysis of Algorithms Tutorial 2 Chengyu Lin

Outline ·Graph Concepts Single-source shortest path problem Breadth-first search for unweighted graphs 。 Dijkstra's algorithm for non-negative weights
Outline • Graph Concepts • Single-source shortest path problem • Breadth-first search – for unweighted graphs • Dijkstra’s algorithm – for non-negative weights

Graph ·G=(V,E) 0 Simple graph:unweighted,undirected graph, containing no loops and multiple edges o IEl =O(IV12) P 02 30 O ●6 01 ●
Graph • G = (V, E) • Simple graph: unweighted, undirected graph, containing no loops and multiple edges o |E| = O(|V|2 ) 1 2 3 4 5 6 7
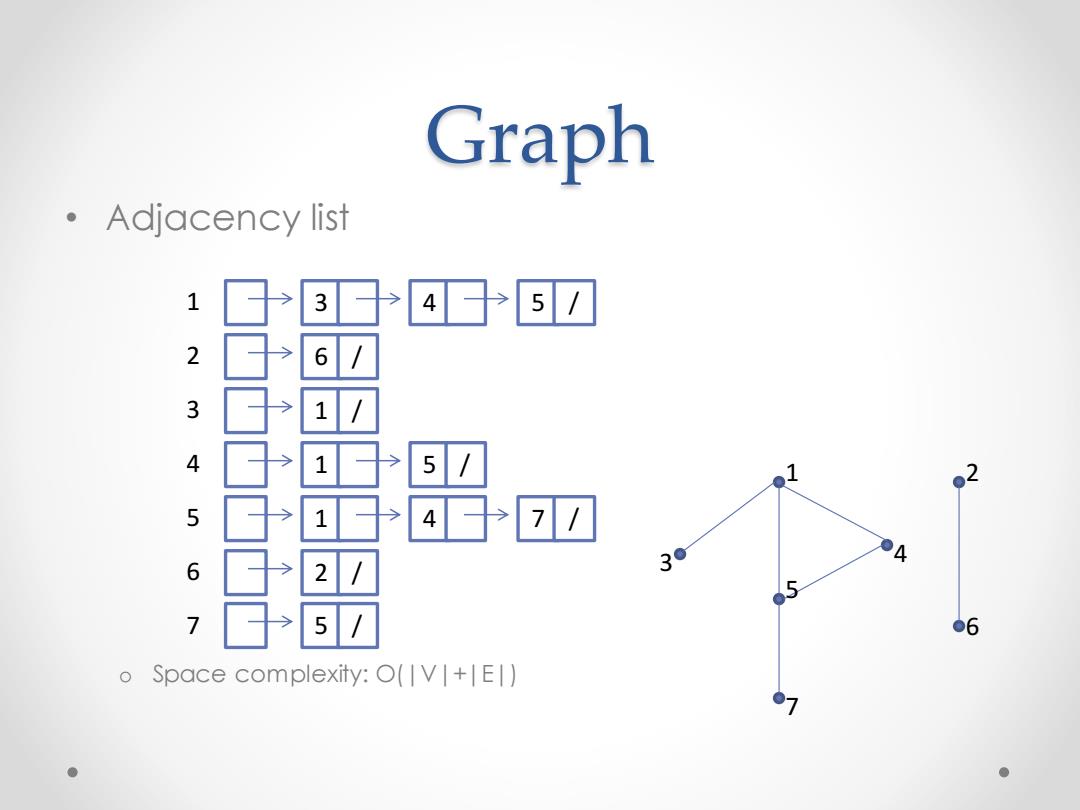
Graph Adjacency list 1 345/ 2 6/ 3 4 1日于5/ 02 5 1日于4日于7U 2/ 30 A 6 7 ☐50 ●6 Space complexity:O(V+E) ●
Graph • Adjacency list o Space complexity: O(|V|+|E|) 1 2 3 4 5 6 7 3 4 5 / 6 / 1 / 1 5 / 1 4 7 / 2 / 5 / 1 2 3 4 5 6 7

Single-source shortest path What is the optimal path from one vertex to another? o Suppose each edge is of unit length o Store the minimum distances in an array dist[ 0 Example:if source vertexs ="3" dist[u] o! u 03 1 1 30 e4 2 0∞ 3 0 6 4 2 5 2 1 6 ● ● 7 3
Single-source shortest path • What is the optimal path from one vertex to another? o Suppose each edge is of unit length o Store the minimum distances in an array dist[] o Example: if source vertex s = “3” 1 2 3 4 5 6 7 u dist[u] 1 1 2 ∞ 3 0 4 2 5 2 6 ∞ 7 3

Breadth-first search(BFS) Intuition:find the neighbors of the neighbors Additional structure:a queue Q ·Pseudocode: o Initialize: ·dist[s】=O;dist[u=∞for all other vertices u o Q=[s] o While Q is not empty Dequeue the top element u of Q 。For all neighbors v of u,if dist[v]=∞, o Put v in Q o Set dist[v]=dist[u]+1 ● ●
Breadth-first search (BFS) • Intuition: find the neighbors of the neighbors • Additional structure: a queue Q • Pseudocode: o Initialize: • dist[s] = 0; dist[u] = ∞ for all other vertices u o Q = [s] o While Q is not empty • Dequeue the top element u of Q • For all neighbors v of u, if dist[v] = ∞, o Put v in Q o Set dist[v] = dist[u] + 1
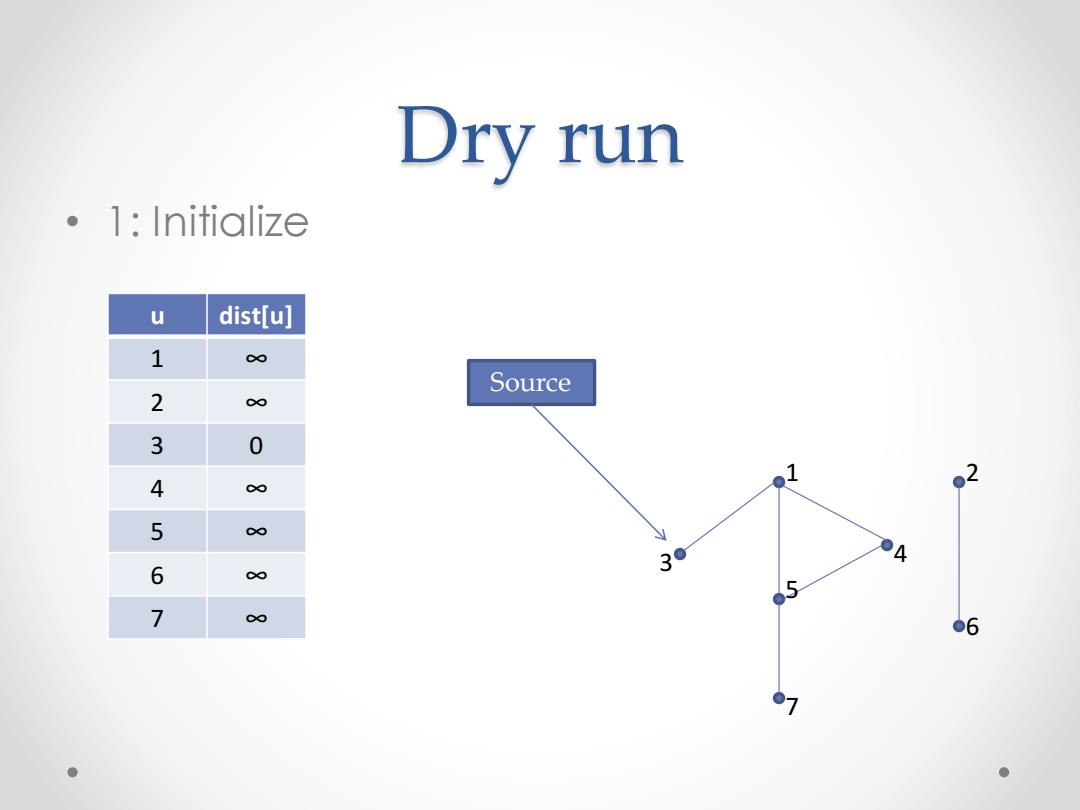
Dry run 。1:Initialize u dist[u] 1 ∞ Source 2 ∞ 3 0 4 02 5 30 ok 6 o 7 c ●6 。1 ●
Dry run • 1: Initialize 1 2 3 4 5 6 7 u dist[u] 1 ∞ 2 ∞ 3 0 4 ∞ 5 ∞ 6 ∞ 7 ∞ Source s
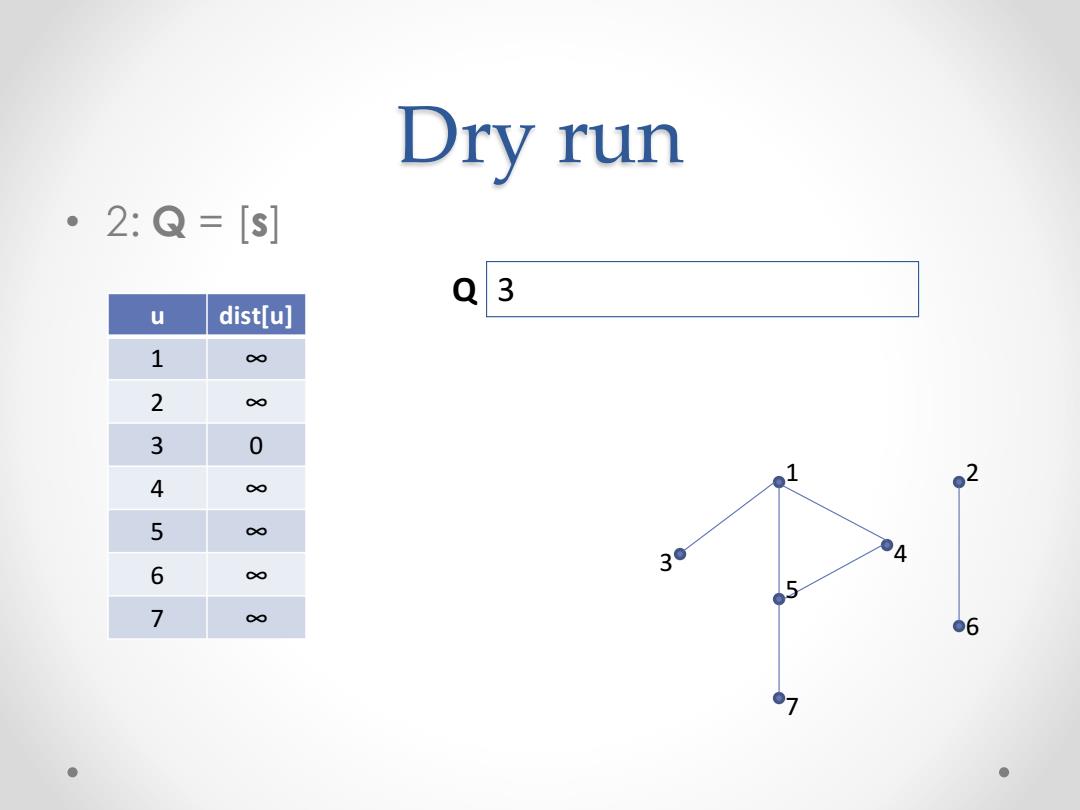
Dry run 2:Q=[s] Q 3 u dist[u] 1 ∞ 2 3 0 4 0 5 e 6 c∞ 30 7 c∞ ●6 01 ●
Dry run • 2: Q = [ s ] 1 2 3 4 5 6 7 u dist[u] 1 ∞ 2 ∞ 3 0 4 ∞ 5 ∞ 6 ∞ 7 ∞ Q 3 1 4 5 7
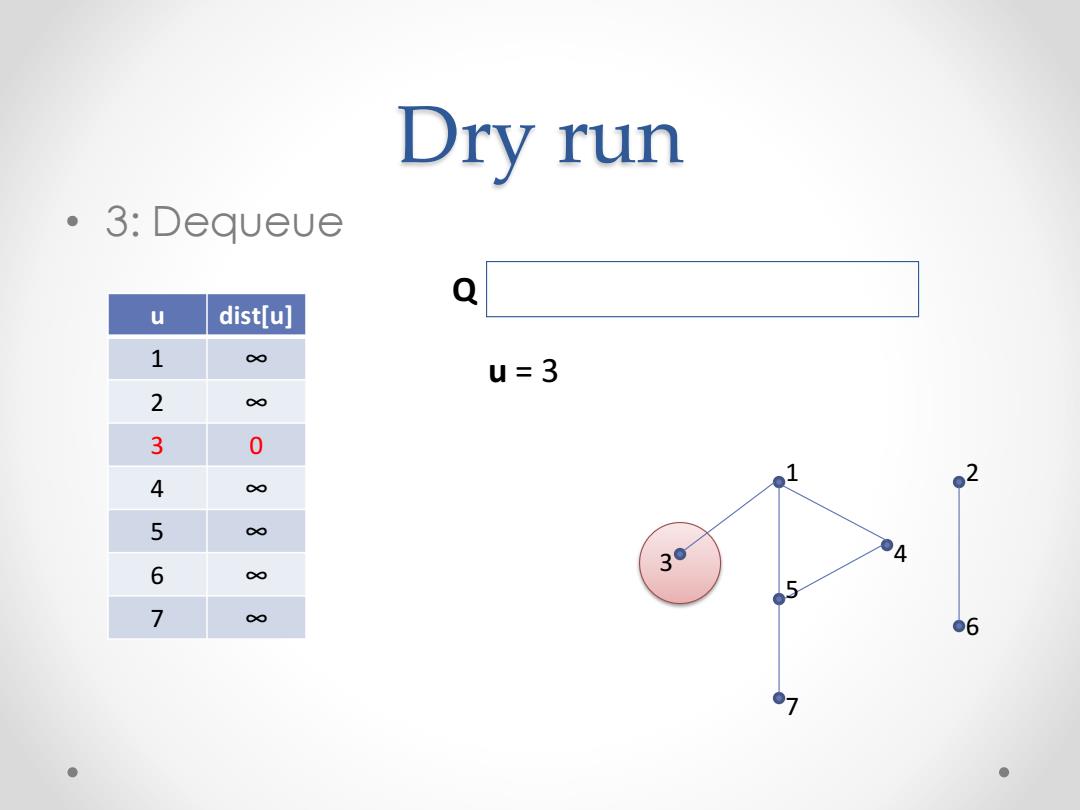
Dry run ·3:Dequeue Q u dist[u] 1 ∞ u=3 2 ∞ 3 0 4 ∞ 03 5 Jo OA 6 G∞ 7 c∞ ●6 01 ●
Dry run • 3: Dequeue 1 2 3 4 5 6 7 u dist[u] 1 ∞ 2 ∞ 3 0 4 ∞ 5 ∞ 6 ∞ 7 ∞ Q 3 1 4 5 7 u = 3
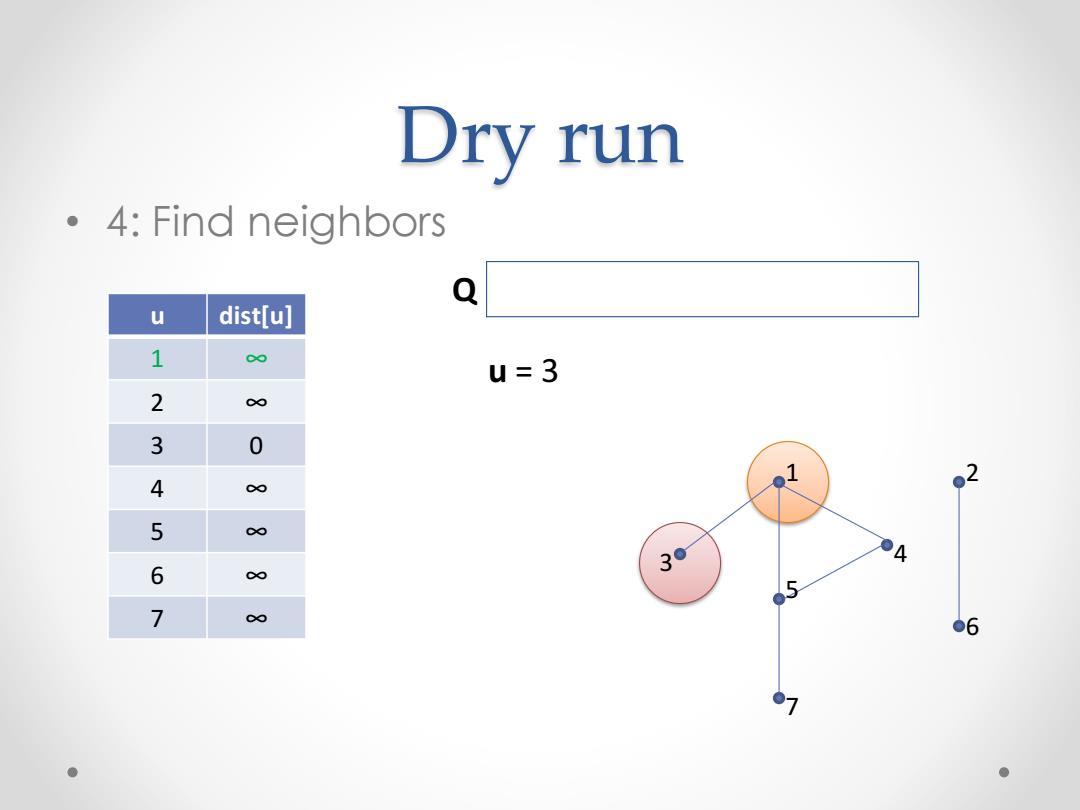
Dry run 。4:Find neighbors Q u dist[u] 1 0∞ u=3 2 ∞ 3 0 4 P 02 5 e 6 ∞ Jo 7 C∞ ●6 。1 ●
Dry run • 4: Find neighbors 1 2 3 4 5 6 7 u dist[u] 1 ∞ 2 ∞ 3 0 4 ∞ 5 ∞ 6 ∞ 7 ∞ Q 3 1 4 5 7 u = 3