
CSCI 3160 Design and Analysis of Algorithms Tutorial 8 Chengyu Lin
CSCI 3160 Design and Analysis of Algorithms Tutorial 8 Chengyu Lin

Maximum Network Flow Maximize the flow from the source to the sink 561w M人 Disclaimer:Most of the slides are taken from last year's tutorial of this course
Maximum Network Flow • Maximize the flow from the source to the sink Disclaimer: Most of the slides are taken from last year’s tutorial of this course

Network Flow 3/3 ·Capacity constraint 3/3 2/2 Flow value(nonnegative)on an edge 0/2 1/4 (u,v)cannot exceed c(u,v) 2/3 3/3 2/2 。Flow conservation Incoming Outgoing 5/30 No leakage 20/40 NO! 15/30 06
Network Flow • Capacity constraint – Flow value (nonnegative) on an edge (u,v) cannot exceed c(u,v) • Flow conservation – Incoming = Outgoing – No leakage 20/40 5/30 15/30
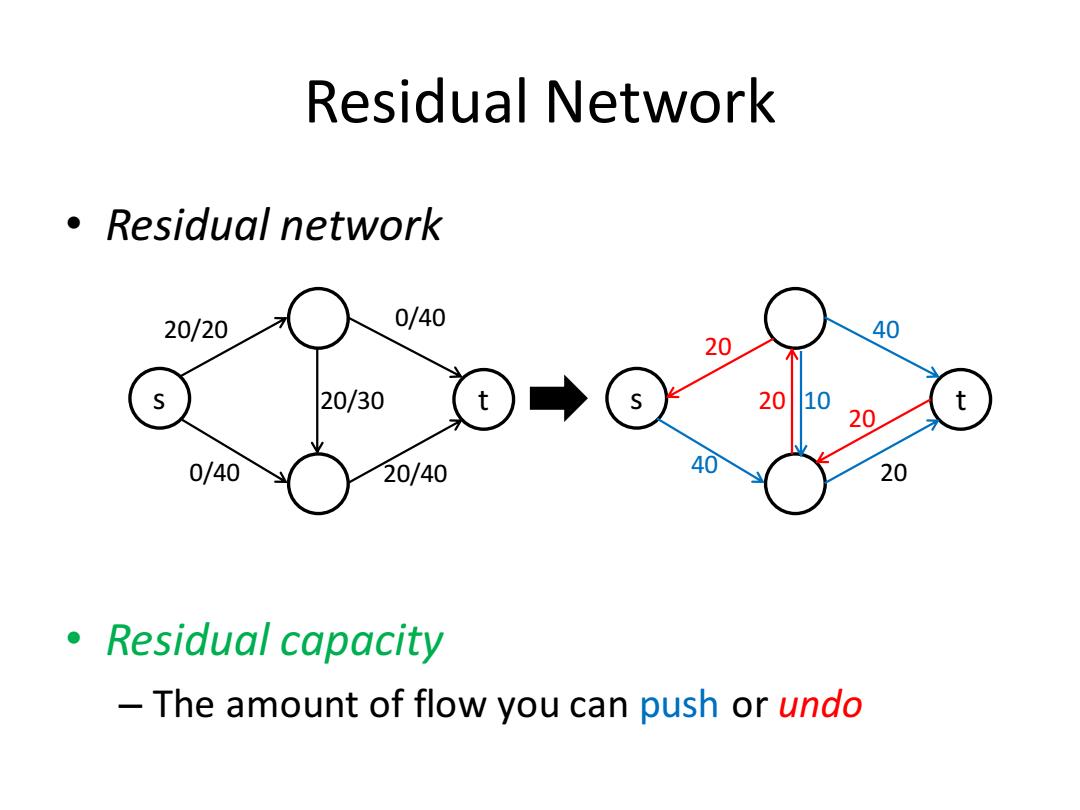
Residual Network ·Residual network 20/20 0/40 40 20 20/30 t 2010 20 0/40 20/40 40 20 。Residual capacity The amount of flow you can push or undo
Residual Network • Residual network • Residual capacity – The amount of flow you can push or undo s t 40 20 40 20 20 20 s t 20/20 0/40 20/40 0/40 20/30 10

Augmenting path A path from source to sink in the residual network Different ways of finding augmenting path yield different performances Method Complexity Ford-Fulkerson DFS (|E|maxlfl) Edmonds-Karp BFS O(IVIJE12)
Augmenting path • A path from source to sink in the residual network • Different ways of finding augmenting path yield different performances Method Complexity Ford-Fulkerson DFS O(|E| max|f|) Edmonds-Karp BFS O(|V||E| 2 )

How slow can Ford-Fulkerson be? 0/9999 0/9999 0/1 t 0/9999 0/9999 0 绝
How slow can Ford-Fulkerson be? s t 0/9999 0/9999 0/9999 0/9999 0/1
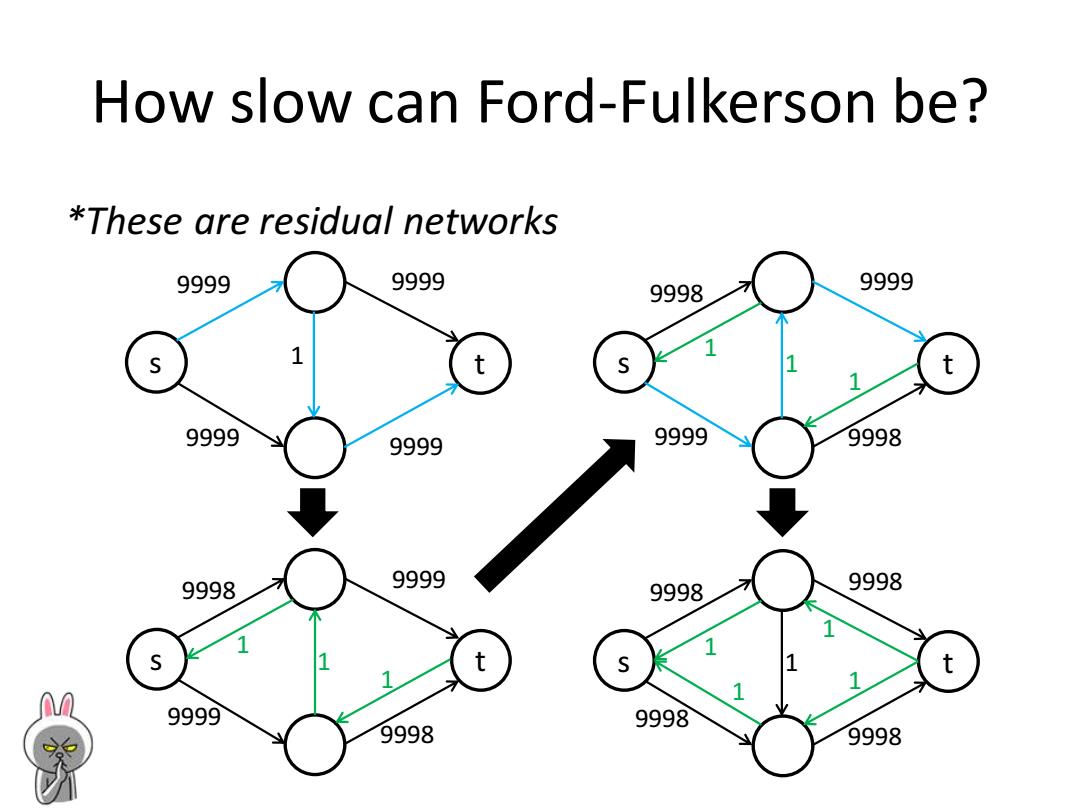
How slow can Ford-Fulkerson be? *These are residual networks 9999 9999 9998 9999 s 1 t 9999 9999 9999 9998 9998 9999 9998 9998 t t M 9999 9998 9998 9998
How slow can Ford-Fulkerson be? *These are residual networks s t 9999 9999 9999 9999 1 s t 9998 9999 9998 9999 1 1 1 s t 9998 9999 9998 9999 1 1 1 s t 9998 9998 9998 9998 1 1 1 1 1
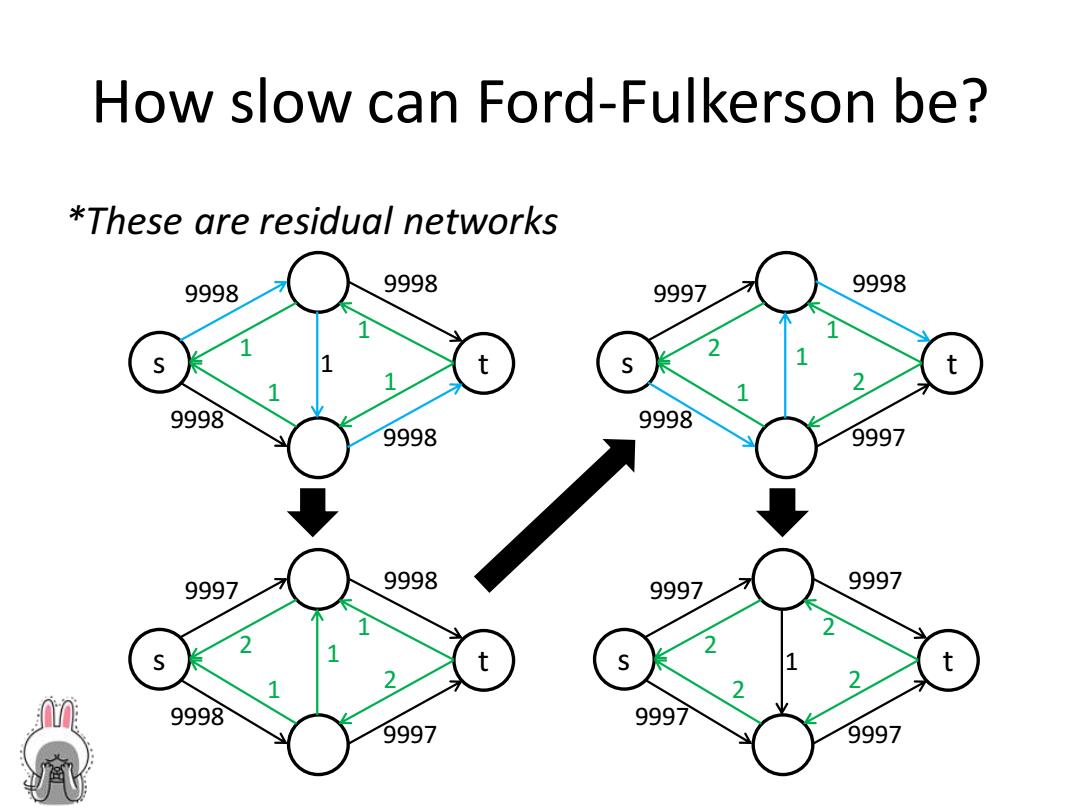
How slow can Ford-Fulkerson be? *These are residual networks 9998 9998 9997 9998 9998 9998 9998 9997 9997 9998 9997 9997 t t 9998 9997 9997 9997
How slow can Ford-Fulkerson be? *These are residual networks s t 9998 9998 9998 9998 1 1 1 1 1 s t 9997 9998 9997 9998 2 2 1 1 1 s t 9997 9998 9997 9998 2 2 1 1 1 s t 9997 9997 9997 9997 1 2 2 2 2
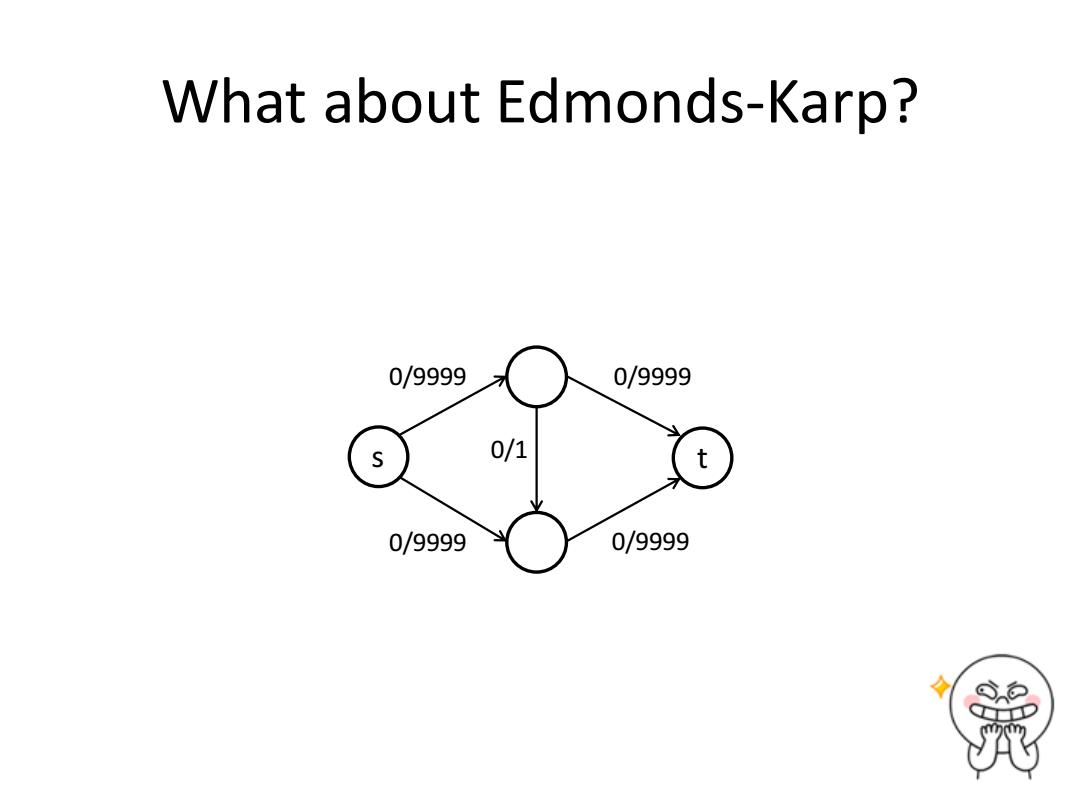
What about Edmonds-Karp? 0/9999 0/9999 0/1 t 0/9999 0/9999
What about Edmonds-Karp? s t 0/9999 0/9999 0/9999 0/9999 0/1
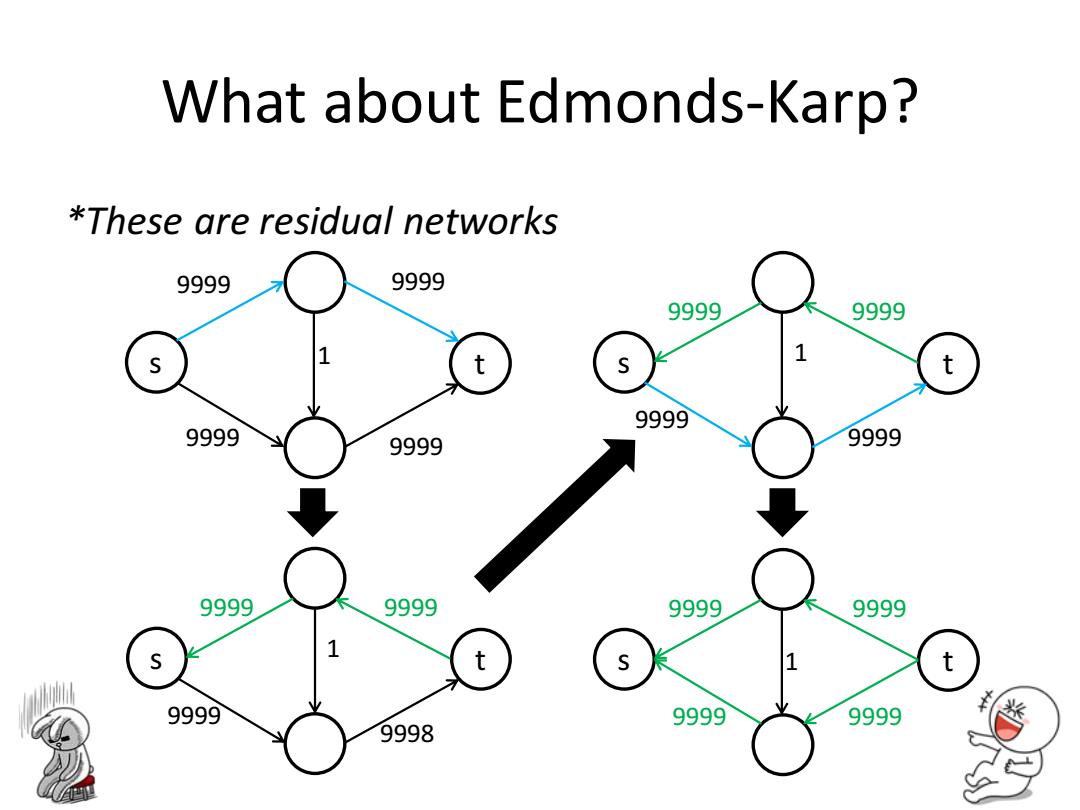
What about Edmonds-Karp? *These are residual networks 9999 9999 9999 9999 1 s 1 t t 9999 9999 9999 9999 9999 9999 9999 9999 1 十 s 1 t 9999 9999 9999 9998
What about Edmonds-Karp? *These are residual networks s t 9999 9999 9999 9999 1 s t 9999 9998 9999 1 9999 s t 9999 9999 9999 1 9999 s 1 t 9999 9999 9999 9999