
CSC3160: Design and Analysis of Algorithms Week 3: Greedy Algorithms Instructor: Shengyu Zhang 1
Instructor: Shengyu Zhang 1

Content Two problems Minimum Spanning Tree Huffman encoding One approach:greedy algorithms 2
Content ◼ Two problems ❑ Minimum Spanning Tree ❑ Huffman encoding ◼ One approach: greedy algorithms 2

Example 1:Minimum Spanning Tree 3
Example 1: Minimum Spanning Tree 3
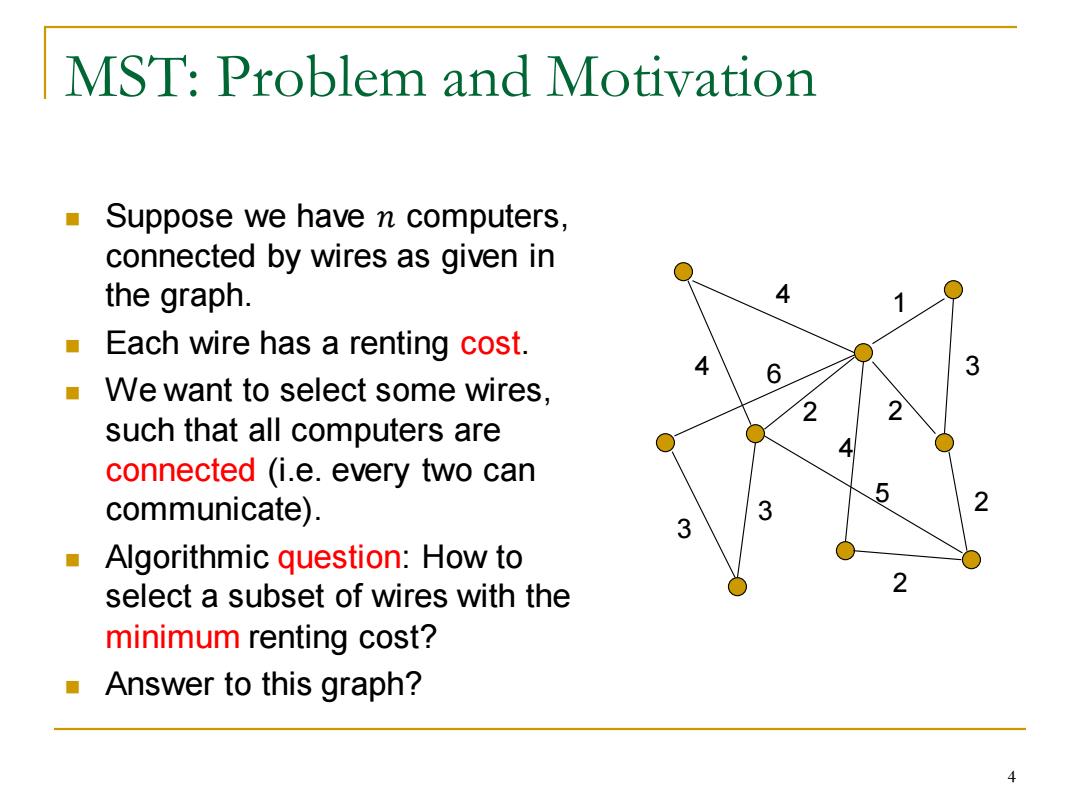
MST:Problem and Motivation Suppose we have n computers, connected by wires as given in the graph. 4 1 ■ Each wire has a renting cost. 4 6 3 ■ We want to select some wires, such that all computers are connected (i.e.every two can communicate). 3 Algorithmic question:How to select a subset of wires with the minimum renting cost? Answer to this graph?
MST: Problem and Motivation ◼ Suppose we have 𝑛 computers, connected by wires as given in the graph. ◼ Each wire has a renting cost. ◼ We want to select some wires, such that all computers are connected (i.e. every two can communicate). ◼ Algorithmic question: How to select a subset of wires with the minimum renting cost? ◼ Answer to this graph? 4 1 4 3 5 4 2 2 2 3 3 2 6 4
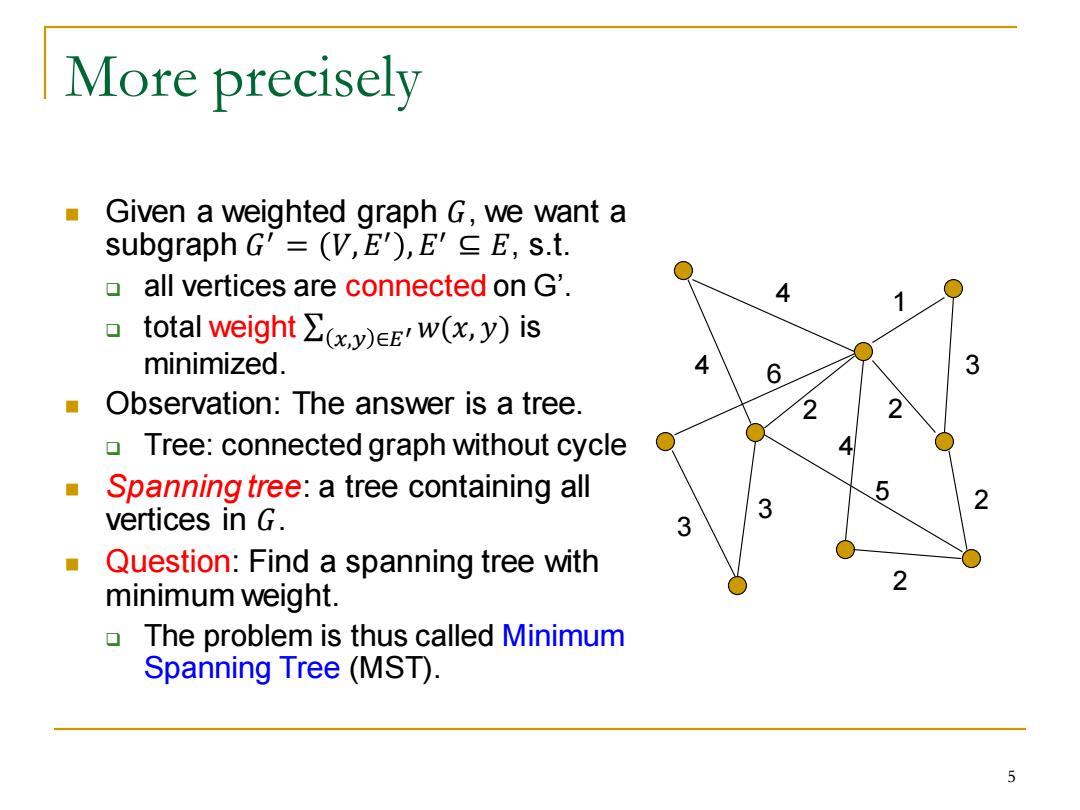
More precisely Given a weighted graph G,we want a subgraph G'=(V,E),E'C E,s.t. all vertices are connected on G'. 4 1 0 total weight (w(x,y)is minimized. 4 6 3 Observation:The answer is a tree. 2 Tree:connected graph without cycle Spanning tree:a tree containing all vertices in G. 3 3 Question:Find a spanning tree with 2 minimum weight. The problem is thus called Minimum Spanning Tree (MST). 5
More precisely ◼ Given a weighted graph 𝐺, we want a subgraph 𝐺 ′ = 𝑉,𝐸 ′ ,𝐸 ′ ⊆ 𝐸, s.t. ❑ all vertices are connected on G’. ❑ total weight σ 𝑥,𝑦 ∈𝐸′ 𝑤(𝑥, 𝑦) is minimized. ◼ Observation: The answer is a tree. ❑ Tree: connected graph without cycle ◼ Spanning tree: a tree containing all vertices in 𝐺. ◼ Question: Find a spanning tree with minimum weight. ❑ The problem is thus called Minimum Spanning Tree (MST). 4 1 4 3 5 4 2 2 2 3 3 2 6 5
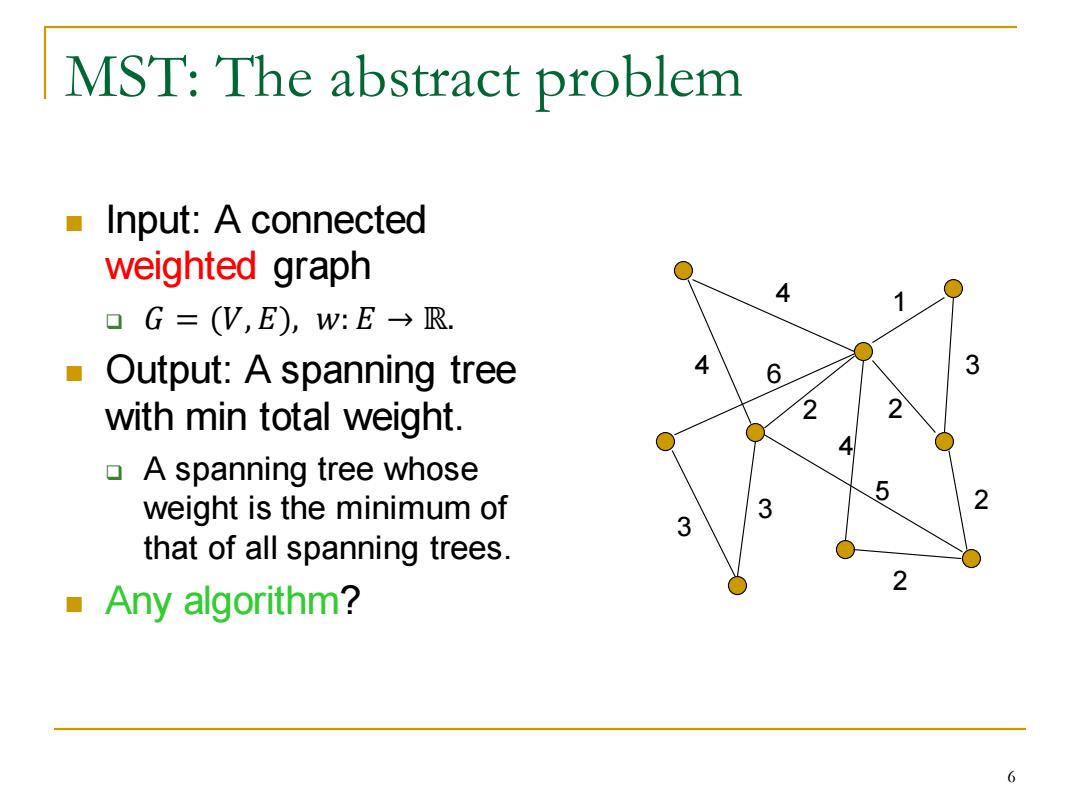
MST:The abstract problem Input:A connected weighted graph 4 1 口G=(V,E),w:E→R. Output:A spanning tree 4 6 3 with min total weight. 2 2 ▣A spanning tree whose weight is the minimum of 2 3 that of all spanning trees. Any algorithm? 6
MST: The abstract problem ◼ Input: A connected weighted graph ❑ 𝐺 = (𝑉, 𝐸), 𝑤: 𝐸 → ℝ. ◼ Output: A spanning tree with min total weight. ❑ A spanning tree whose weight is the minimum of that of all spanning trees. ◼ Any algorithm? 4 1 4 3 5 4 2 2 2 3 3 2 6 6

Methodology 4:Starting from a naive solution 0 See whether it works well enough If not,try to improve it. A first attempt may not be correct ■ But that's fine.The key is that it'll give you a chance to understand the problem
◼ Methodology 4: Starting from a naïve solution ❑ See whether it works well enough ❑ If not, try to improve it. ◼ A first attempt may not be correct ◼ But that’s fine. The key is that it’ll give you a chance to understand the problem. 7
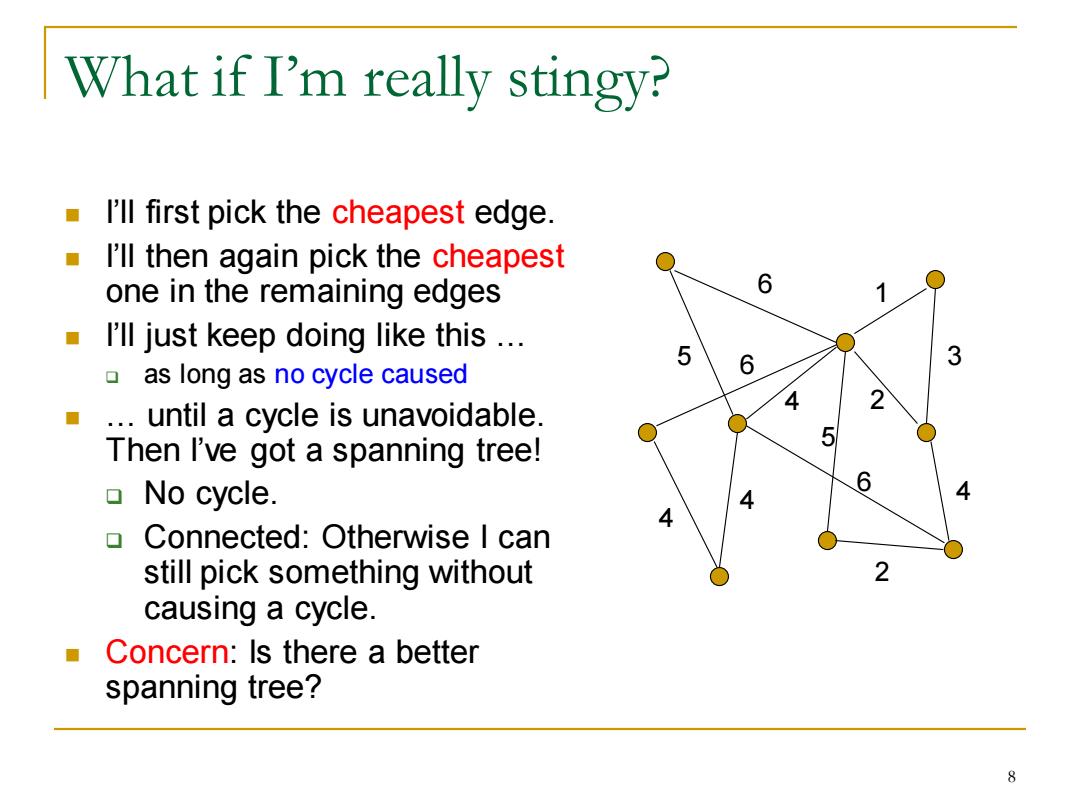
What if I'm really stingy? I'll first pick the cheapest edge. I'll then again pick the cheapest one in the remaining edges 6 1 I'll just keep doing like this .. 5 6 3 as long as no cycle caused ..until a cycle is unavoidable. 4 Then I've got a spanning tree! No cycle. Connected:Otherwise I can still pick something without causing a cycle. Concern:Is there a better spanning tree? 8
What if I’m really stingy? ◼ I’ll first pick the cheapest edge. ◼ I’ll then again pick the cheapest one in the remaining edges ◼ I’ll just keep doing like this … ❑ as long as no cycle caused ◼ … until a cycle is unavoidable. Then I’ve got a spanning tree! ❑ No cycle. ❑ Connected: Otherwise I can still pick something without causing a cycle. ◼ Concern: Is there a better spanning tree? 6 1 5 4 6 5 4 2 4 3 4 2 6 8

Kruskal's Algorithm What we did just now is Kruskal's algorithm. Repeatedly add the next lightest edge that doesn't produce a cycle... in case of a tie,break it arbitrarily ...until finally reaching a tree ---that's the answer!
Kruskal's Algorithm ◼ What we did just now is Kruskal’s algorithm. ❑ Repeatedly add the next lightest edge that doesn't produce a cycle… ◼ in case of a tie, break it arbitrarily. ❑ …until finally reaching a tree --- that’s the answer! 9
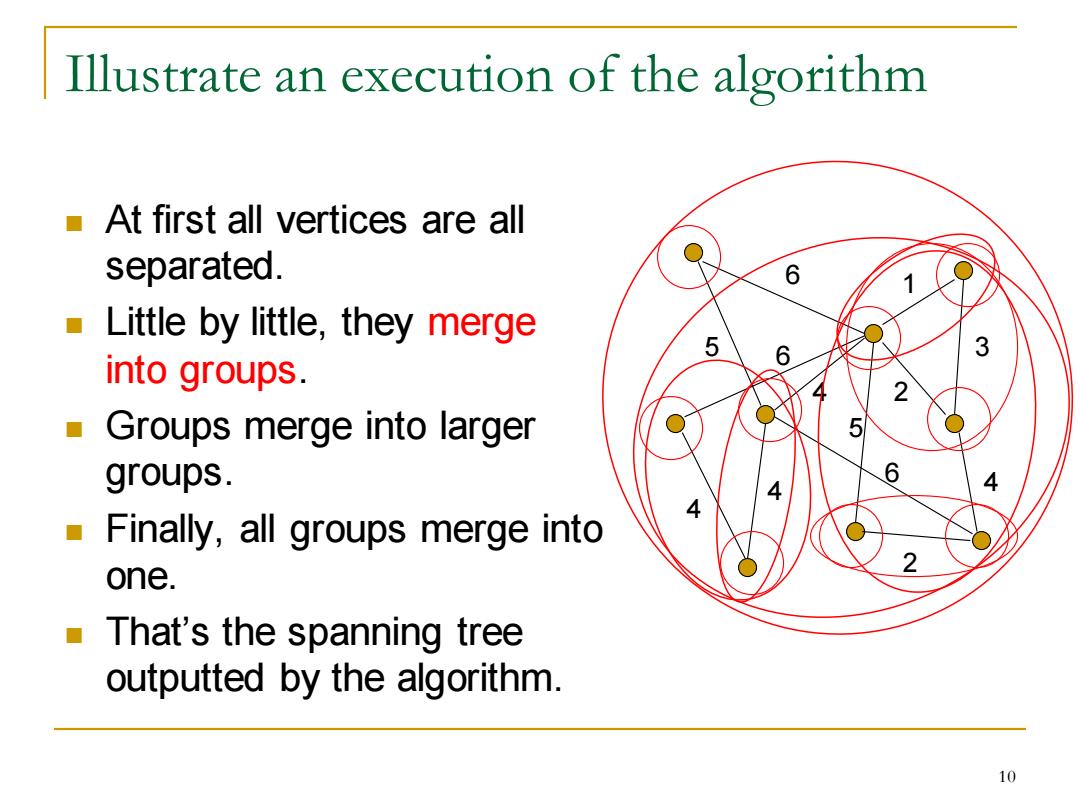
Illustrate an execution of the algorithm -At first all vertices are all separated. Little by little,they merge 5 into groups. Groups merge into larger groups. Finally,all groups merge into one. o That's the spanning tree outputted by the algorithm. 10
Illustrate an execution of the algorithm ◼ At first all vertices are all separated. ◼ Little by little, they merge into groups. ◼ Groups merge into larger groups. ◼ Finally, all groups merge into one. ◼ That’s the spanning tree outputted by the algorithm. 6 1 5 4 6 5 4 2 4 3 4 2 6 10