
第六章基本检索与周游方法
第六章 基本检索与周游方法

·问题描述 ·许多涉及到二元树、树和图的问题 ●】 涉及问题中数据结点的访问和处理 有的问题需要访问结构中所有结点,有的 访问结构的部分结点。 ·本章介绍的方法将适用于树、二元树,有 些方法可以用于图、树、二元树
• 问题描述 • 许多涉及到二元树、树和图的问题 • 涉及问题中数据结点的访问和处理 • 有的问题需要访问结构中所有结点,有的 访问结构的部分结点。 • 本章介绍的方法将适用于树、二元树,有 些方法可以用于图 、树、二元树

6.1一般方法 1.检索与周游 检索:以某种方法检查给定的数据对象,找出满足 某些给定性质的结点的过程称为检索 周游:当检索过程必须检索到数据对象的每一个结 点时,则该检索过程称为周游 访问结点:当算法对一个结点的信息段进行处理时, 称该结点被访问。 结点被访问可以是结点被打印、或作某种处理
6.1 一般方法 1.检索与周游 检索:以某种方法检查给定的数据对象,找出满足 某些给定性质的结点的过程称为检索 周游:当检索过程必须检索到数据对象的每一个结 点时,则该检索过程称为周游 访问结点:当算法对一个结点的信息段进行处理时, 称该结点被访问。 结点被访问可以是结点被打印、或作某种处理

2.二元树周游(遍历) 1)周游次序 在二元树的周游中,以D、L、R分别代表访问结点 的信息段、访问左子树、访问右子树。则可能的顺序有: ★LDR:中根次序周游(中根遍历) ★LRD:后根次序周游(后根遍历) ★DLR:先根次序周游(先根遍历) ★RDL:逆中根次序周游 ★RLD:逆后根次序周游 ★DRL:逆先根次序周游
2. 二元树周游(遍历) 1)周游次序 在二元树的周游中,以D、L、R分别代表访问结点 的信息段、访问左子树、访问右子树。则可能的顺序有: ★ LDR:中根次序周游(中根遍历) ★ LRD:后根次序周游(后根遍历) ★ DLR:先根次序周游(先根遍历) ★ RDL:逆中根次序周游 ★ RLD:逆后根次序周游 ★ DRL:逆先根次序周游

2)二元树周游算法 (1)中根次序周游 算法6.1中根次序周游的递归表示 procedure INORDER(T) //T是一棵二元树。T的每个结点有三个信息 段:LCHILD,DATA,RCHILD// ifT≠0then cal1 INORDER (LCHILD(T)) call VISIT(T) ca11 INORDER(RCHILD(T)) endif end INORDER
2)二元树周游算法 ⑴ 中根次序周游 算法6.1 中根次序周游的递归表示 procedure INORDER(T) //T是一棵二元树。T的每个结点有三个信息 段:LCHILD,DATA,RCHILD// if T≠0 then call INORDER(LCHILD(T)) call VISIT(T) call INORDER(RCHILD(T)) endif end INORDER

(2)先根次序周游 算法6.2先根次序周游的递归表示 procedure PREORDER(T) //T是一棵二元树。T的每个结点有三个信 息段:LCHILD,DATA,RCHILD// ifT≠0then call VISIT(T) cal1 PREORDER(LCHILD(T)) cal1 PREORDER(RCHILD(T)) endif end preORDER
⑵先根次序周游 算法6.2 先根次序周游的递归表示 procedure PREORDER(T) //T是一棵二元树。T的每个结点有三个信 息段:LCHILD, DATA,RCHILD// if T≠0 then call VISIT(T) call PREORDER(LCHILD(T)) call PREORDER(RCHILD(T)) endif end PREORDER

(2)后根次序周游 算法6.3后根次序周游的递归表示 procedure POSTORDER(T) //T是一棵二元树。T的每个结点有三个信 息段:LCHILD,DATA,RCHILD// fT≠0then cal1 POSTORDER(LCHILD(T)) cal1 POSTORDER(RCHILD(T) call VISIT(T) endif end preorder
⑵后根次序周游 算法6.3 后根次序周游的递归表示 procedure POSTORDER(T) //T是一棵二元树。T的每个结点有三个信 息段:LCHILD,DATA,RCHILD// if T≠0 then call POSTORDER(LCHILD(T)) call POSTORDER(RCHILD(T)) call VISIT(T) endif end PREORDER
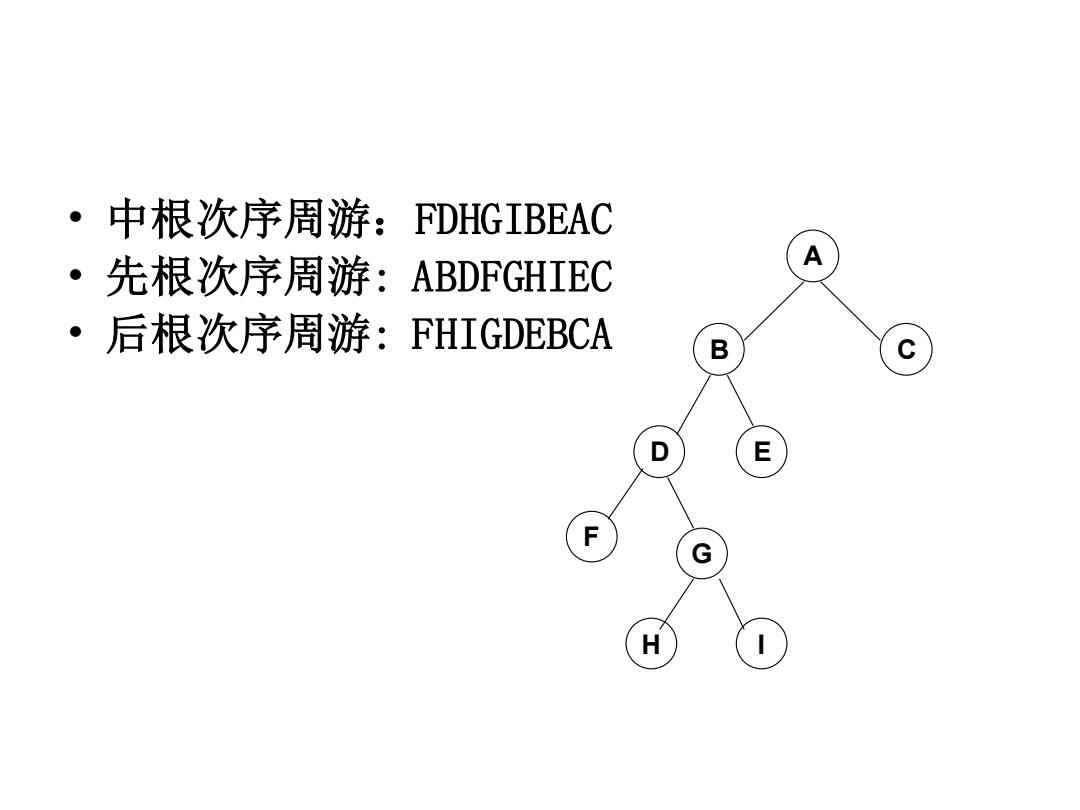
·中根次序周游:FDHGIBEAC 。 先根次序周游:ABDFGHIEC A ·后根次序周游:FHIGDEBCA B C D E F G H
• 中根次序周游:FDHGIBEAC • 先根次序周游: ABDFGHIEC • 后根次序周游: FHIGDEBCA A B D E G C H F I

注 棵二元树可由中根遍历序列十先根遍历序列、 或中根遍历序列十后根遍历序列唯一确定。但不能 由先根遍历序列十后根遍历序列唯一确定。 如已知一棵二元树的中根遍历次序是: DGBEAFHC 先根遍历次序是:ABDGECFH A 则这棵二元树唯一确定如下: B C D E F G H
注: 一棵二元树可由中根遍历序列+先根遍历序列、 或中根遍历序列+后根遍历序列唯一确定。但不能 由先根遍历序列+后根遍历序列唯一确定。 如已知一棵二元树的中根遍历次序是: DGBEAFHC 先根遍历次序是:ABDGECFH 则这棵二元树唯一确定如下: A B D E G C F H

定理6.1当输入的树T有n≥0个结点时,设t(n)和s(n)分别表示这些 周游算法中的任意一个算法所需要的最大时间和空间。如果访问一个 结点所需要的时间和空间是⊙(1),则t(n)=⊙(n),s(n)=⊙(n)。 证明: 时间:由于已知访问一个结点所需时间是⊙(1),故可用常数c限界。 设T的左子树中的结点数是n1,则t(n)有: t (n)=maxni{t (n1)+t (n-n1-1)+ci}n>1 其中,t(0)≤c1 归纳法证明t(n)≤c2n+c1,其中c2是一使得c2≥2c1的常数。 1)当n=0时,成立 2)假定当n=0,1,…,m-1时均成立。则当n=m时有, 设T是一棵有m个结点的树,T左子树结点数为n1,则 t (n)=maxni{t (n1)+t(n-n1-1)+c1} <maxniic2n1+c1+c2(n-n1-1)+ci+c1} =maxn1ic2n+3c1-c2 ≤c2n+c1 同理,存在c'2和c'1有t(n)≥c'2n+c'1。所以t(n)=⊙(n) 空间:若T的深度为d,则所需空间为⊙(d),d≤n,所以s(n)=⑧(n)
定理6.1 当输入的树T有n≥0个结点时,设t(n)和s(n)分别表示这些 周游算法中的任意一个算法所需要的最大时间和空间。如果访问一个 结点所需要的时间和空间是Θ(1),则t(n)=Θ(n), s(n)=Θ(n)。 证明: 时间:由于已知访问一个结点所需时间是Θ(1),故可用常数c1限界。 设T的左子树中的结点数是n1,则t(n)有: t(n)=maxn1{t(n1)+t(n-n1-1)+c1} n≥1 其中,t(0)≤c1。 归纳法证明t(n)≤c2n+c1,其中c2是一使得c2≥2c1的常数。 1)当n=0时,成立 2)假定当n=0,1,…,m-1时均成立。则当n=m时有, 设T是一棵有m个结点的树,T左子树结点数为n1,则 t(n)=maxn1{t(n1)+t(n-n1-1)+c1} ≤maxn1{c2n1+c1+c2(n-n1-1)+c1+c1} =maxn1{c2n+3c1-c2} ≤c2n+c1 同理,存在c'2和c'1有t(n)≥c'2n+c'1。所以t(n)=Θ(n) 空间:若T的深度为d,则所需空间为Θ(d), d≤n,所以s(n)=Θ(n)