
第五章 平面图形的几何性质 §5-1 静矩和形心 §5一2惯性矩惯性积惯性半径 §5-3 平行移轴公式 §5-4 转轴公式 §5-5 主惯性轴主惯性矩形心心主惯性轴及 形心主惯性柜
第五章 平面图形的几何性质 §5-1 静矩和形心 §5-2 惯性矩 惯性积 惯性半径 §5-3 平行移轴公式 §5-5 主惯性轴 主惯性矩 形心主惯性轴及 形心主惯性矩 §5-4 转轴公式

应力的计算通常用要到构件截面的几何参数 拉压正应力 -A-j 621 扭转切应力 -可a
拉压正应力 A N = A = dA 扭转切应力 p I T = = A I p dA 2 应力的计算通常用要到构件截面的几何参数
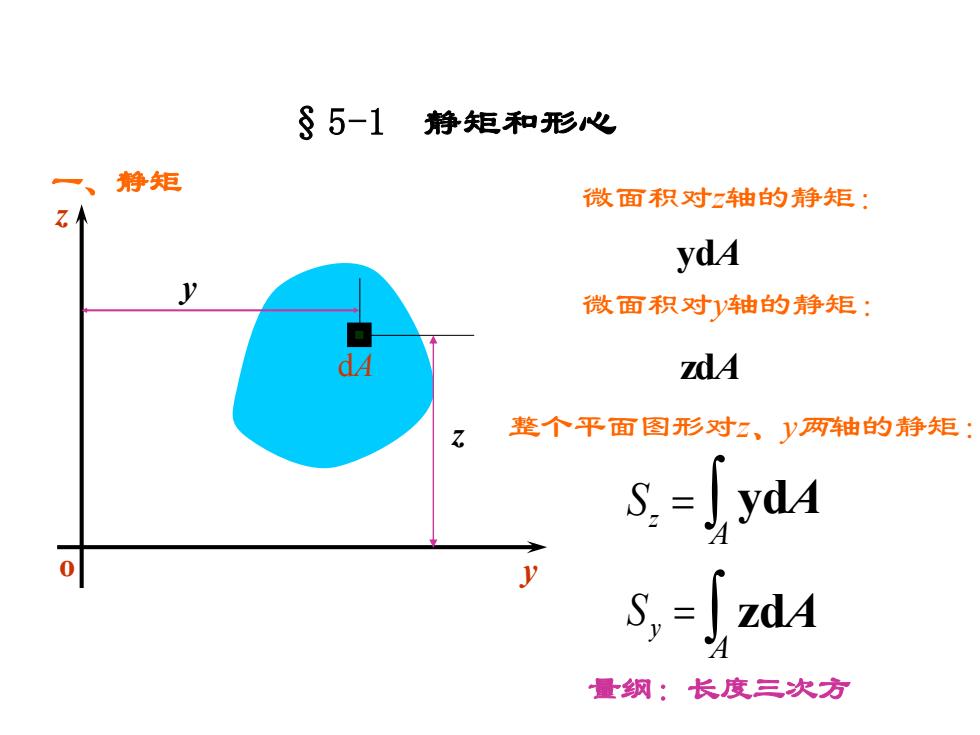
§5-1静矩和形心 一、静矩 微面积对2轴的静矩: ydA 微面积对y轴的静矩: zdA 整个平面图形对二、y两轴的静矩: s.-[yda 0 s,=z4 量纲:长度三次方
§5-1 静矩和形心 一、静矩 o y z y z A Sz = ydA A Sy = zdA 量纲:长度三次方 dA 微面积对z轴的静矩: ydA 微面积对y轴的静矩: zdA 整个平面图形对z、y两轴的静矩:

形心C的坐标: ydA y A 「dA zdA = A dA S.=Ay Sy=A匠 表明:平面图形对某一轴的静矩等于图形面积乘以相应的形心坐标。 若S2=0和S。=0,则少=0和豆=0。可见,若图形对某一轴 的静矩等于零,则该轴必然通过图形的形心;反之,若某一轴通过 形心,则图形对该轴的静矩等于零
表明:平面图形对某一轴的静矩等于图形面积乘以相应的形心坐标。 o y z C 形心 C 的坐标: = = dA zdA A S z y = = dA ydA A S y z z y S Az S Ay y = z = 若 和 ,则 和 。可见,若图形对某一轴 的静矩等于零,则该轴必然通过图形的形心;反之,若某一轴通过 形心,则图形对该轴的静矩等于零。 Sz = 0 Sy = 0 y = 0 z = 0

三、组合图形的静矩和形心 工 常见的一些组合图形 整个图形对某一轴的惯矩静矩等于各个简单图形 对同一轴的静矩的代数和。P955-1
三、组合图形的静矩和形心 常见的一些组合图形 整个图形对某一轴的惯矩静矩等于各个简单图形 对同一轴的静矩的代数和。 P95 5-1
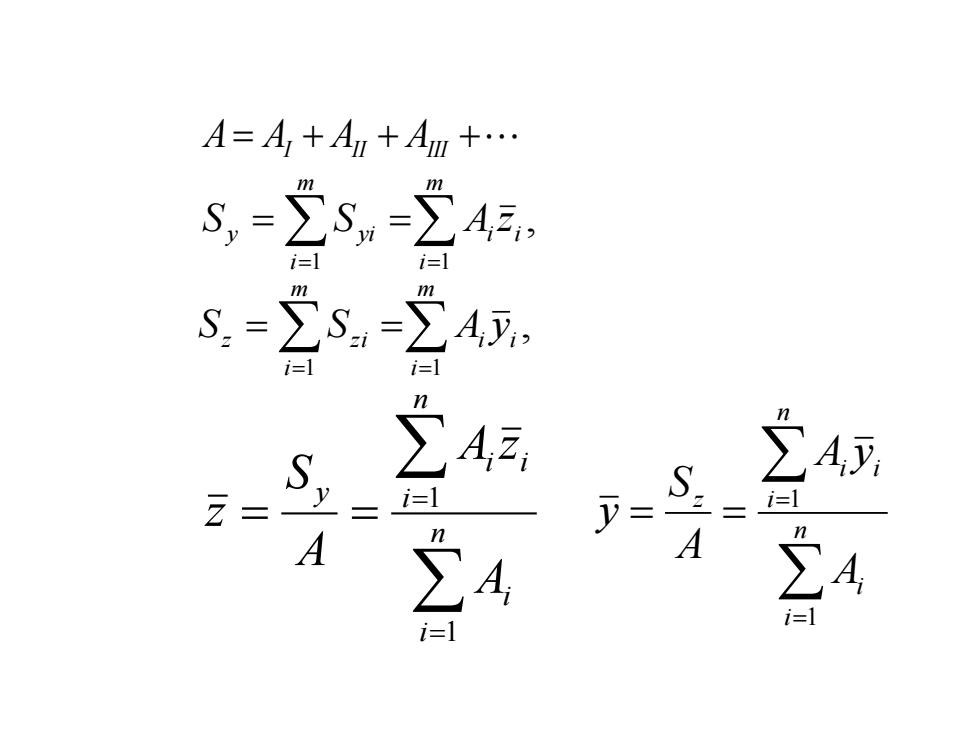
A=A+Au+Am+. m S,=」 A,21 i=l i=1 m S.- D zi A, =1 i=l n S 4,2 S A i=] A A ∑4 A i=1
A= AI + AII + AIII + , 1 1 = = = = m i i i m i y yi S S A z = = = = n i i n i i i z A A y A S y 1 1 = = = = n i i n i i i y A A z A S z 1 1 , 1 1 = = = = m i i i m i z z i S S A y

例1求图示半圆形的形心心位置 由对称性,只需求乞。 现取平行于y轴的狭长条作为微面积。 dA=ydz=2vR2-z2dz 正 s,-M=2r-=R R 0 2 R3 图1-2 4R A R2 3元 2
例1 求图示半圆形的形心位置 z 由对称性,只需求 。 现取平行于y轴的狭长条作为微面积。 z dA ydz 2 R z dz 2 2 = = − 3 0 2 2 3 2 S zdA z 2 R z dz R R A y = = − = = = = 3 4R R 2 1 R 3 2 A S z 2 3 y

§5-2 惯性矩惯性积惯性半径 一、惯性矩、惯性半径 微面积对z轴的惯性矩: y2dA 微面积对y轴的惯性矩: 2dA y 整个平面图形对z、V两轴的惯性矩 dA 0 1,=y2d4 1,=2dA 量纲:长度四次方
§5-2 惯性矩 惯性积 惯性半径 o y z y z dA 一、惯性矩、惯性半径 A y 2 I z = dA A z 2 I y = dA 量纲:长度四次方 微面积对z轴的惯性矩: y 2dA 微面积对y轴的惯性矩: z 2dA 整个平面图形对z、y两轴的惯性矩:

工程上,经常把惯性矩写成图形面积与某 一长度平方的乘积,即 1y=Ai1=A 或改写为 式中,iy、12分别称为图形对轴和z轴的惯性半径,其量纲为长度
工程上,经常把惯性矩写成图形面积与某 一长度平方的乘积,即 或改写为 2 y Ai y I = 2 z Aiz I = A I i y y = A I i z z = y i z 式中, 、 i 分别称为图形对y轴和z轴的惯性半径,其量纲为长度

平面图形对坐标原 点的极惯性矩: lp =S P'dA dA 。=J4p2dA=∫2+z2h =S'dA+y'da 0 =I+I. 图形对于任意一对互相垂直轴的惯性矩之和,等 于它对该两轴交点的极惯性矩
= A I dA 2 o y z y z dA 平面图形对坐标原 点的极惯性矩: ( ) y z A A A A I I z dA y dA I dA y z dA = + = + = = + 2 2 2 2 2 图形对于任意一对互相垂直轴的惯性矩之和,等 于它对该两轴交点的极惯性矩