
第六章拉弯和压弯构件 。第一节拉弯、压弯构件的应用及截面形式 ·第二节拉弯、压弯构件的强度和计算 ·第三节实腹式压弯构件的整体稳定 ·第四节实腹式压弯构件的局部稳定 ·第五节压弯构件的设计 第六节拉弯构件的计算 。第七节双向压弯构件的计算 第八节偏心受压柱柱头和柱脚的构造与计算
第六章 拉弯和压弯构件 第一节 拉弯、压弯构件的应用及截面形式 第二节 拉弯、压弯构件的强度和计算 第三节 实腹式压弯构件的整体稳定 第四节 实腹式压弯构件的局部稳定 第五节 压弯构件的设计 第六节 拉弯构件的计算 第七节 双向压弯构件的计算 第八节 偏心受压柱柱头和柱脚的构造与计算
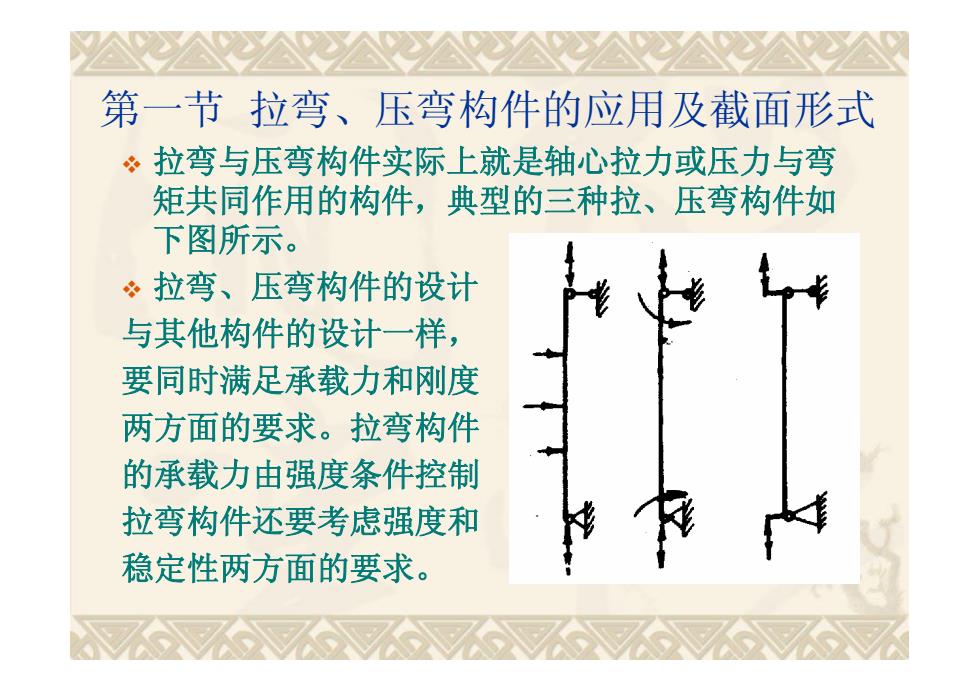
第一节拉弯、压弯构件的应用及截面形式 ·拉弯与压弯构件实际上就是轴心拉力或压力与弯 矩共同作用的构件,典型的三种拉、压弯构件如 下图所示。 。拉弯、压弯构件的设计 与其他构件的设计一样, 要同时满足承载力和刚度 两方面的要求。拉弯构件 的承载力由强度条件控制 拉弯构件还要考虑强度和 稳定性两方面的要求
第一节 拉弯、压弯构件的应用及截面形式 拉弯与压弯构件实际上就是轴心拉力或压力与弯 矩共同作用的构件,典型的三种拉、压弯构件如 下图所示。 拉弯、压弯构件的设计 与其他构件的设计一样, 要同时满足承载力和刚度 两方面的要求。拉弯构件 的承载力由强度条件控制 拉弯构件还要考虑强度和 稳定性两方面的要求

拉弯、压弯构件的截面形式甚多,一般可分型钢 截面和组合截面两类,二组合截面又分为实腹式和格 构式两种截面 T工工工T四 图6.3拉弯、压鸟构件的酸真形式
拉弯、压弯构件的截面形式甚多,一般可分型钢 截面和组合截面两类,二组合截面又分为实腹式和格 构式两种截面
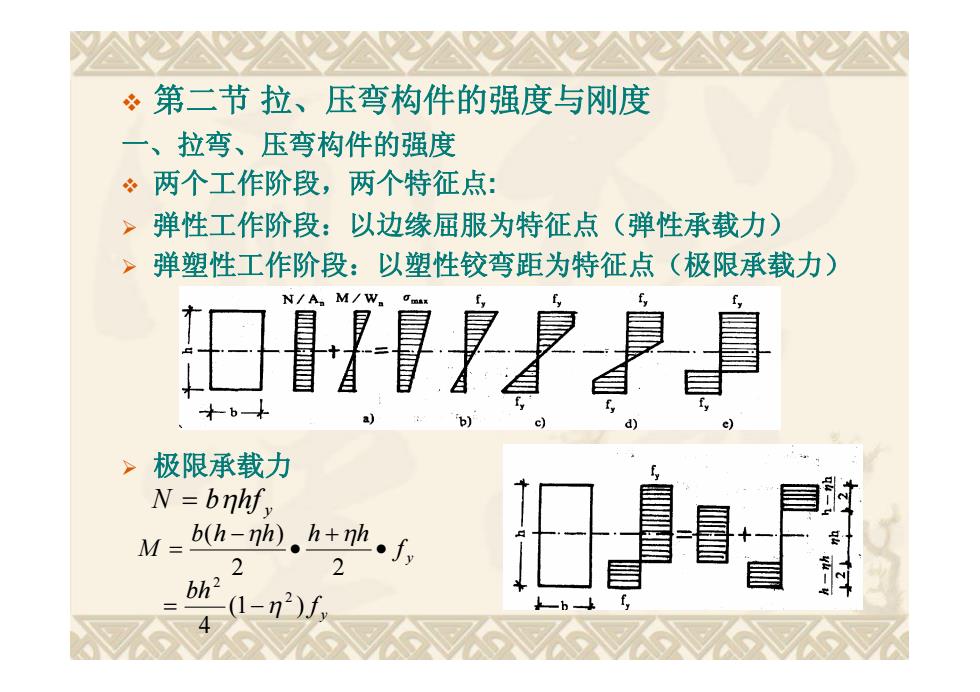
。第二节拉、压弯构件的强度与刚度 一、拉弯、压弯构件的强度 。两个工作阶段,两个特征点: >弹性工作阶段:以边缘屈服为特征点(弹性承载力) 弹塑性工作阶段:以塑性铰弯距为特征点(极限承载力) >极限承载力 N=bnhfy M=b(h-nh)h+nh 2 2 bh2 (1-n2)f 4
第二节 拉、压弯构件的强度与刚度 一、拉弯、压弯构件的强度 两个工作阶段,两个特征点: 弹性工作阶段:以边缘屈服为特征点(弹性承载力) 弹塑性工作阶段:以塑性铰弯距为特征点(极限承载力) 极限承载力 N bhf y y f bh (1 ) 4 2 2 y f b h h h h M 2 2 ( )
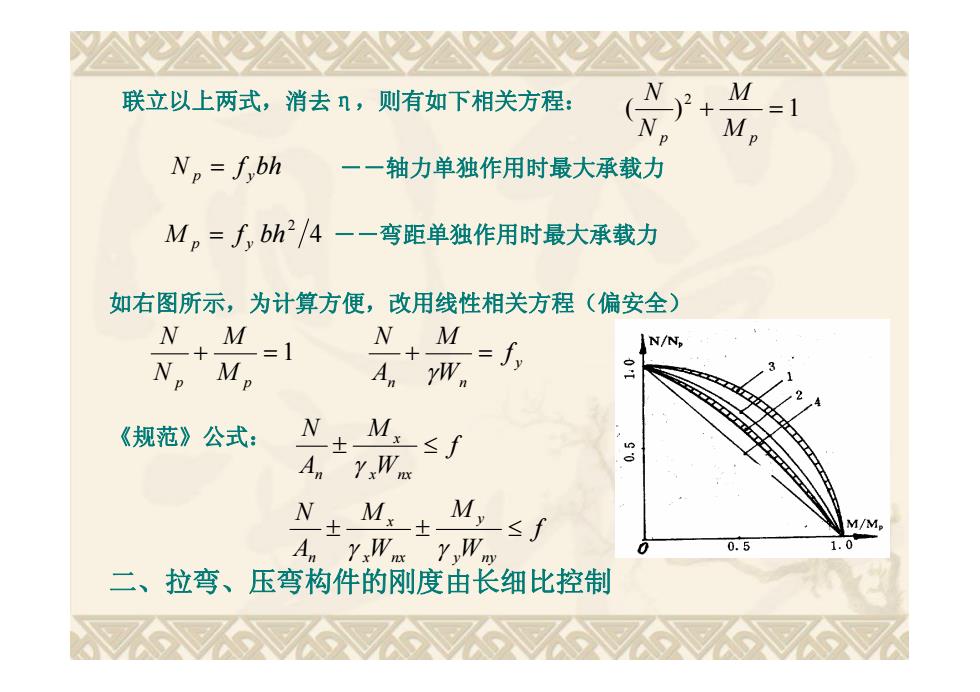
联立以上两式,消去1,则有如下相关方程: +, =1 Np=f bh 一一轴力单独作用时最大承载力 M=f bh2/4 一一弯距单独作用时最大承载力 如右图所示,为计算方便,改用线性相关方程(偏安全) NM =1 N M =f N/N N。M, A YW 《规范》公式: N±M:≤f An YW N+M±M,sf M/M A.rWr W 0.5 二、拉弯、压弯构件的刚度由长细比控制
联立以上两式,消去η,则有如下相关方程: --轴力单独作用时最大承载力 --弯距单独作用时最大承载力 如右图所示,为计算方便,改用线性相关方程(偏安全) 《规范》公式: 二、拉弯、压弯构件的刚度由长细比控制 ( ) 1 2 p M p M N N N f bh p y 4 2 M f bh p y 1 p M p M N N y n n f W M A N f W M A N x nx x n f W M W M A N y ny y x nx x n

第三节实腹式压弯构件的整体稳定 实腹式压弯构件在轴力及弯距作用下,即可能发生弯矩 作用平面内的弯曲失稳,也可能发生弯矩作用平面外的弯曲 扭转失稳(类似梁)。两方面在设计中均应保证。 、 实腹式压弯构件在弯矩作用平面内的稳定性 N M. A Wis(1-2N/N) 根据弯矩等效原理考虑等效弯矩系数: N BreM ≤ A W:(1-0N/Ne) 引入抗力分项系数: BM PA h1W.(1-0.8N/Na)
第三节 实腹式压弯构件的整体稳定 实腹式压弯构件在轴力及弯距作用下,即可能发生弯矩 作用平面内的弯曲失稳,也可能发生弯矩作用平面外的弯曲 扭转失稳(类似梁)。两方面在设计中均应保证。 一、实腹式压弯构件在弯矩作用平面内的稳定性 根据弯矩等效原理考虑等效弯矩系数: 引入抗力分项系数: y x x Ex x x f W N N M A N (1 ) 1 f W N N M A N x x Ex mx x x (1 ) ' 1 f W N N M A N x x Ex mx x x (1 0.8 ) ' 1 1

第四节实腹式压弯构件的局部稳定 规范对压弯构件的局部稳定计算仍以板件的屈曲为准则,用 限制板件宽(高)厚比来保证板件的稳定性,见表6.1 表 面及板件尺 宽(高)厚比值 ≤1s 角解板底和方距使现速受拉的了用积面 当ae1.0时,A/(成,A后52357 5a.>10时,A/C度s,%,A,0)e、235 写第使夏擦受压的T数解:A么≤(15+02A√235 当0≤g1.6时.AA.≤(16+0.sa+2s入三 当16c2时,A.≤4+054一2k2)、2 0G1523577 A,s的2☑ 当0=年1.6时,人A.0.1,+05h+25入25 当16eag2时人,04线+05A-2益2)257 但上满式的右赠不小于相, 4/r≤I0o2353
第四节 实腹式压弯构件的局部稳定 规范对压弯构件的局部稳定计算仍以板件的屈曲为准则,用 限制板件宽(高)厚比来保证板件的稳定性,见表6.1

第五节压弯构件的设计 。一、实腹式压弯构件的截面设计 1、截面形式的选择 2、截面的初步选择 3、验算截面 1)强度 2)刚度 3)整体稳定性 4)局部稳定性 4、构造要求
第五节 压弯构件的设计 一、实腹式压弯构件的截面设计 1、截面形式的选择 2、截面的初步选择 3、验算截面 1)强度 2)刚度 3)整体稳定性 4)局部稳定性 4、构造要求

二、格构式压弯构件的截面设计 1、截面的初步选择 当弯矩不大时,可以用双对称的截面形式[如下图中的 (a)、(b)]:如果弯矩较大时,可以用单轴对称的截面[如 下图中的(c)、(d)],并将较大的脂件放在压力较大的一 侧
二、格构式压弯构件的截面设计 1、截面的初步选择 当弯矩不大时,可以用双对称的截面形式[如下图中的 (a)、(b)];如果弯矩较大时,可以用单轴对称的截面[如 下图中的(c)、(d)],并将较大的脂件放在压力较大的一 侧

2、截面验算 1)强度 2)整体稳定性 弯矩作用平面内的稳定性 :N BM 0,AW.1-0,N/N) 弯矩作用平面外的稳定性:这种情况下,可不计 算平面外的整体稳定性,但要求计算分肢的稳定性。 3)分肢稳定性 单肢1: N=M+w /O 单肢2: N,=N-N 4)刚度验算 3、缀材设计 4、构造要求
2、截面验算 1)强度 2)整体稳定性 弯矩作用平面内的稳定性: 弯矩作用平面外的稳定性:这种情况下,可不计 算平面外的整体稳定性,但要求计算分肢的稳定性。 3)分肢稳定性 单肢1: 单肢2: 4)刚度验算 3、缀材设计 4、构造要求 f W N N M A N x x Ex mx x x (1 ) ' 1 a y N a M N x 2 1 N2 N N1