
试卷代号:1024 座位号■■ 中央广播电视大学2006一2007学年度第二学期“开放本科”期末考试 计算机专业 信号处理原理 试题 2007年7月 题 号 三 四 五 六 总 分 分数 得 分 评卷人 一、判断对错(对在括号内写“正确”,错则在括号内写“错误”。每小 题3分,共15分)】 1.指数信号的微分结果不是指数信号。 () 2.如果信号在(一∞,0)开区间内信号取值均为0,则该信号为因果信号。 () 3.信号傅立叶变换的尺度变换特性表明:时域压缩对应频域扩展、时域扩展对应频域压 缩。 ()) 4.实信号的傅里叶变换的幅度频谱一定是偶函数。 5.序列ZT的ROC是以极点为边界,一定包含其极点。 得 分 评卷人 二、单项选择题(每小题5分,共25分) 1.8-)= 6(t)(选择合适的结果作为冲激函数前面的系数)。() A.3 B.1/3 C.-3 D.-1/3 2.下面的叙述正确的是()。 A.时域信号f(t)的FT存在的充分条件是时域信号f(t)绝对可积 B.要保证无失真的恢复原始信号,抽样频率不能超过信号最高频率的两倍 C.离散信号的幅度谱也是离散的 D.若信号x(t)为实信号,则其幅度谱是ω的奇函数 174
试卷代号:1024 座位号厂工习 中央广播电视大学2006-2007学年度第二学期“开放本科”期末考试 计算机专业 信号处理原理 试题 2007年 7月 题 号 四 五 六 总 分 分 数 得 分 评卷人 一、判断对错(对在括号 内写“正确”,错则在括号 内写“错误”。每小 题 3分,共 15分) 指数信号的微分结果不是指数信号。 ( ) 如果信号在(一二 ,o>开区间内信号取值均为 。,则该信一号为因果信 号。 ( ) 信号傅立叶变换的尺度变换特性表 明:时域压缩对应频域扩展、时域扩展对应频域压、、 二 了 、 J 、 缩 实信号的傅里叶变换的幅度频谱一定是偶函数。 序列 z }}的}zoc是以极点为边界,一定包含其极点。 得 分 评卷人 二、单项选择题(每小题 5分,共 25分) }(-冬 ,} )一— 。(才)(选择合适的结果作为冲激函数前面的系数)。 A. 3 }. 1/3 C.一3 I}.一1/3 下面的叙述正确的是( )。 A.时域信号 f(r)的 F'T存在的充分条件是时域信号‘f (t)绝对可积 B.要保证无失真的恢复原始信号,抽样频率不能超过信号最高频率的两倍 C.离散信号的幅度谱也是离散的 D.若信号 二(<t)为实信号,则其幅度谱是 。的奇函数 174

3.下面关于Sa函数的说法正确的是()。 A.Su函数是奇函数 B.Sa函数在t=0处的值为1 C.Sa函数在t=nπ(n∈Z,n≠0)点处函数值不为0 D.Su(dr= 4.关于离散时间系统,以下说法不正确的是()。 A.不能用差分方程来描述 B.离散时间系统就是输入输出都是序列的系统 C.离散时间系统的传递函数H(x)=Y()/X(x)表示系统的零状态响应与因果序列 激励的ZT之比值 D.离散时间系统响应可以用ZT法求解 5.Z(-1)"w(n)]=()。 A C.:-1 马 得分 评卷人 三、填空题(每小题分,共20分) 1.[f(at)]= 。(a≠0) 3.FT与IFT具有 性,如果两个函数的FT或IFT相等,则这两个函数必然相 ,同时FT具有 性,如果乎[f(t)]=F(),则必有李[F(w)]=f(t),反之亦然。 3.频谱函数F(w)=1所对应的时间函数为(1)= 4.若X()=(-0.5可>0.5),则X(e)对应的时间序列为 5.序列x(n)是 的充要条件是x()=x(n)u(n)。 175
3、下面关于 Su函数 的说法正确的是( )。 A. Su函数是奇函数 13. Su函数在t=。处的值为 1 C. Su函数在t=tzn(nE Z,n}O)点处函数值不为 0 D. J}} 一。〕 Sa (t)d,一粤乙 4,关于离散时间系统,以下说法不正确的是( )。 A.不能用差分方程来描述 B.离散时间系统就是输人输出都是序列的系统 C.离散时间系统的传递 函数 H(z)=Y(z)/X(z)表示系统的零状态响应与因果序列 激励的 ZT之比值 D.离散时间系统响应可以用 ZT法求解 }. Z (一1)"u(,,)1=( )。 一1 。.J)_-1 、、一、。· A 井 二一 1 三、填空题(每小题 飞分 ,共 2}分 ) f' } f(at)] 。(a共 ()) FT与 IFI}具有 性 ,如果两个函数的 }..1.或 IF'I'相等,则这两个函数必然相 右时 厂了具有 性,如果 少}.fct)日二F(}:., ,则必有 r: ' i^f} (c})]二f(t>,反之亦然。 .1频谱函数 F(m)=1所对应的时间函数为 .八门 4.若 X(劝= z (z一 0. 5) (Iz}>o.5),则 X(z)对应的时间序列为 5.序列 二(;‘)是 的充要条件是.,·(,,)一二(,,)。(,‘)· 1i5

得分 评卷人 四、证明题(10分》 证明:如果频谱函数G(w)=π6(w一2)十π6(w+2),那么其所对应的时域信号为g(t)= cos2t。(10分) 得 分 评卷人 五、计算题(每小题10分,共20分)】 1.求信号x(t)=sin2t的傅立叶变换 2.一阶离散系统的差分方程为3y(n)一2y(1一1)=x(n),求: (1)该系统的传递函数H(x) (2)求输人为(n)时系统的零状态响应。 得 分 评卷人 六、作图题(共10分) 画出矩形脉冲信号:f(t)=G2(t)的FT结果图形。 176
得 分 评卷人 四、证明题 (10分 ) 证明:如果频谱函数 G(cu) =}r}(m-2) }-}8(cu-} 2),那么其所对应的时域信号为 }r(t) _ cos2ta(10分) 得 分 评卷人 五、计算题 (每小题 10分 ,共 2.。分) 1.求信号 x(t) = sin2t的傅立叶变换 2.一阶离散系统的差分方程为3贝n)-2贝”一1) =x(}z),求: (1>该 系统的传递 函数 H(z) (2)求输人为 $(n)时系统的零状态响应。 得 分 评卷人 六 、作图题(共 l0分) 画出矩形脉冲信号:f(t> = G}(t)的FT结果图形。 176

试卷代号:1024 中央广播电视大学2006一2007学年度第二学期“开放本科”期未考试 计算机专业信号处理原理试题答案及评分标准 (供参考) 2007年7月 一、是非题(每小题3分,共15分) 1.错误 2.正确 3.正确 4.正确 5.错误 二、单项选择题(每小题5分,共25分) 1.A 2.A 3.B 4.A 5.A 三、填空题(每小题4分,共20分)】 1.F() 2.唯一 可逆 3.6(t) 4.x(n)=(0.5)"u(n) 5.因果序列 四、证明题(10分) 证明:令f(t)=1,那么F(w)=2π8(w) (3分) 根据频谱搬移特性,3[f()cos(2)]-[F(u一2)+F(w+2)] =之×[2xw-2)+2a8w+2] =π8(w-2)+π6(w+2) (4分)》 177
试卷代号 :1024 中央广播电视大学2006-2007学年度第二学期“开放本科”期末考试 计算机专业 信号处理原理 试题答案及评分标准 (供参考) 2007年 7月 一、是非题 (每小题 3分,共 15分) 1. 'ti误 三.正确 3.正确 n.正确 弓 错误 二、单项选择题(每小题 5分 ,共 2}分) 1. A 2. A 三、填空题 (每小题 4分 ,共 20分) 1生二F/里一、 唯一 可逆 8(t) .x}n)= (0. };)"u(,,) 5.因果序列 四、证明题 (10分) 证明:令 f(r>=1,那么 F<m) =2}r8(w) 根据频谱搬移特性,、仁了(t)cos(2t)口一喜 乙 仁F(。一2)-i-F<},}-2)] <3分) 一喜 乙 X r一2}S(。一:)-}-2n8(}-f-2)}一 = n8(。一2 ) -I- nS(。一千2) (4分) 177

由FT的可逆性知,π6(ω一2)+π8(ω十2)所对应的时域函数为g(t)=f(1)cos(2t),f(t) =1, 因此 π6(w一2)十π8(w+2)所对应的时域函数为g(t)=cos(2t) (3分) 五、计算题(共20分】 1.解:x(t)=sin21=e-e (3分) i 因为 1++2π6(w) (2分) 那么,e+2π6(w一an) (2分) 所以,z0=in2=2e-”-[2iu-2)-2aiu+2】 (3分) 24 2.解:根据H(z)的定义,x()为因果序列,系统响应为0状态,因此在方程两边同时进行 Z变换得: 3Y(ε)-2x1Y(≈)=X(x) (4分) 1 H(x)=Y(:)/X(e)=3=22= (2分) 3 (2)输人为6()时系统的零状态响应的Z变换为 Y()-H()X()=3 2[6(]= (2分) z一3 所以,输人为()时系统的零状态响应为: (2分) 六、作图题(共10分)】 答案:矩形信号f(t)=EG,(t),其FT为: -5业=E,:=·s(管)为实函数 178
由}7’的可逆性知,n8(w-2>+ns(W+z)所对应的时域函数为g(t) -f (t)c:os(2t), f(t) i, 因此 nS(。一2)+nS二EGr<t),其FT为: F(m) =)}几}'} .-f(t)e-'}`dt一!r-}zri:F_ e-}`}` dt一厂JI T-/r}.'Z2E (co scat+jsinwt,dt }'r/2。 ,.__。 SLnWt} “ I 乙COS以 GL一 乙 .— 1 J一r1z 田 t =Er·Su }瞥 ,为实函数 \乙 / 110
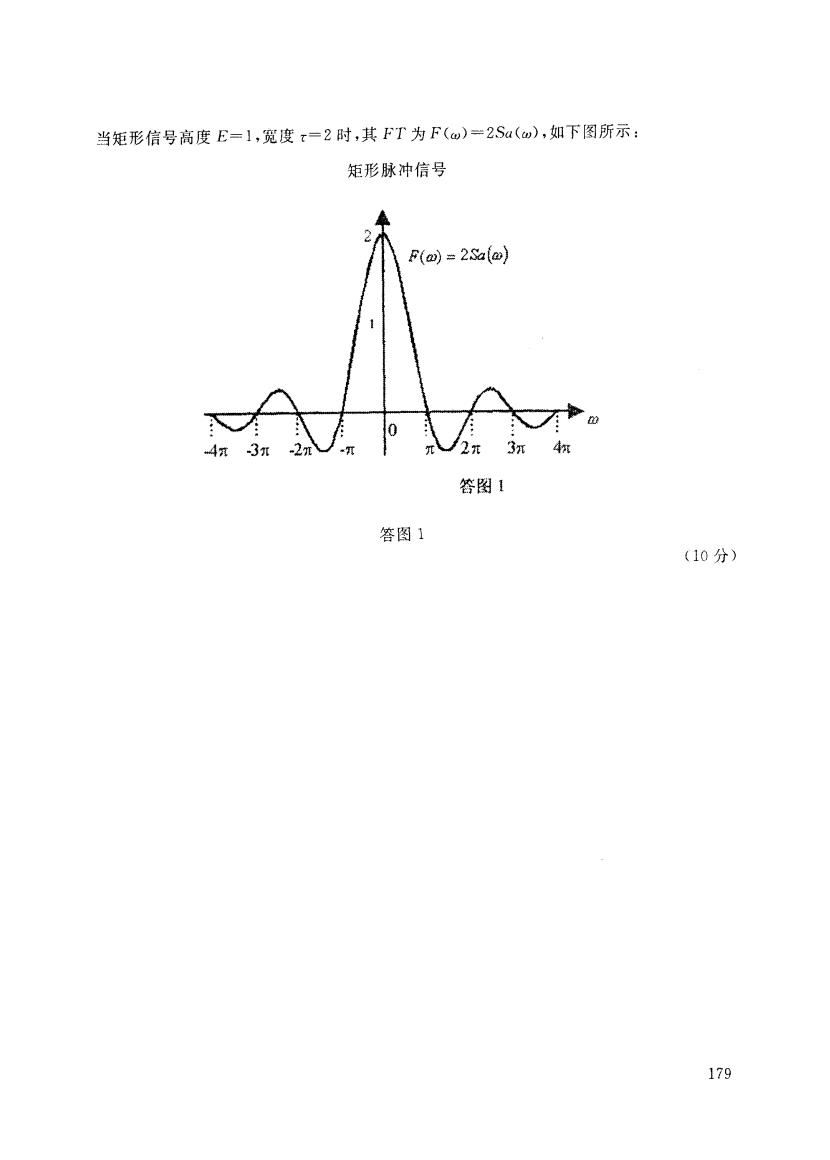
当矩形信号高度E=1,宽度x=2时,其FT为F(w)=2Sa(w),如下图所示: 矩形脉冲信号 2 F(四)=2Sa〔a 0 4克 -3r -2t 3元 答图1 答图1 (10分) 179
当矩形信号高度 E--1,宽度 :=2时,其 F I'为I' ( w)二2Sa(m),如下图所示: 矩形脉冲信号 答图 答 图 1 (10分) 179