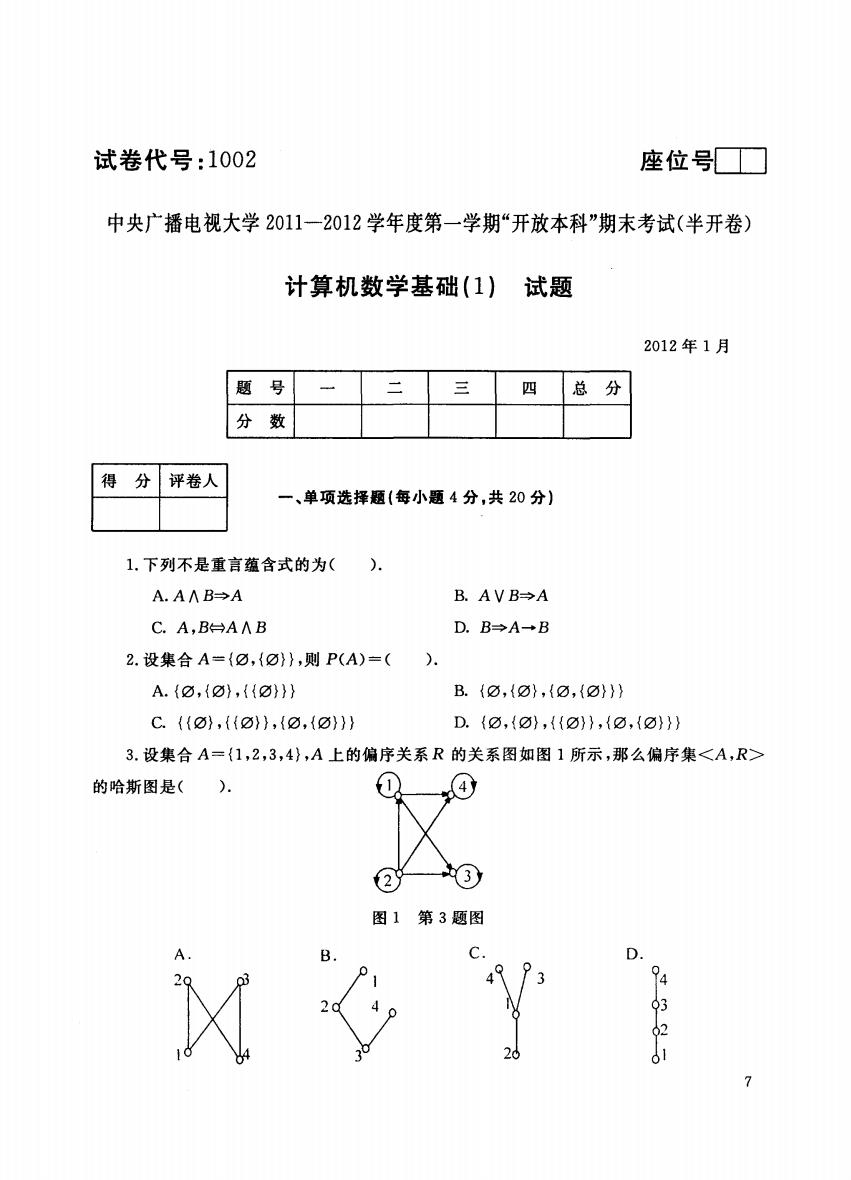
试卷代号:1002 座位号■ 中央广播电视大学2011一2012学年度第一学期“开放本科”期末考试(半开卷) 计算机数学基础(1)试题 2012年1月 题 号 三 四 总分 分数 得 分 评卷人 一、单项选择题(每小题4分,共20分) 1.下列不是重言蕴含式的为( A.A∧B→A B.AVB→A C.A,B曰AAB D.B→A→B 2.设集合A={0,{⑦},则P(A)=( A.{0,{0},{0}} B.{0,{0},{0,{0}} C.{{},{⑦},{0,{0)}} D.{0,{0},{0},{0,{a}} 3.设集合A={1,2,3,4},A上的偏序关系R的关系图如图1所示,那么偏序集 的哈斯图是(). 2 图1第3题图 A B D. 03 93 7
试卷代号 座位号 中央广播电视大学 11 2 0 2学年度第一学期"开放本科"期末考试(半开卷) 计算机数学基础( 1)试题 2012 年1 |题号|一|二|三|四|总分| |分数 I I I I I |得分|评卷人 11 项选 每小 1.下列不是重言蕴含式的为( ). A.AAB=争A B. AVB~A C. ,B D. B~A 2. 集合 ,{0}} ,则 ). A. {白, {臼} , { {臼} } } B. {白, {臼} , {臼, {臼} } } C. {{0} { { } , {白, {臼} } } D. {白, {臼} , { {(} } , {白, } } 3. 设集合 系R 图1 偏序集 的哈斯图是( ). 3题图 D. 7

4.设G是有n个结点,m条边的连通图,必须别去G的( )条边,才能确定G的一棵生 成树. A.m-n+l B.n-m C.m+n+1 D.n-m+l 5.无向图G是欧拉图,当且仅当(). A.G中所有结点的度数全为偶数 B.G中所有结点的度数全为奇数 C.G连通且所有结点的度数全为偶数 D.G连通且所有结点的度数全为奇数 得 分 评卷人 二、填空题(每小题4分,共20分) 6.设F(x):x是鸟,G(x):x会飞翔.则命题“鸟会飞”符号化为 7.命题公式(P→Q)的主析取范式为 8.设集合A={1,2,3,4},B={a,b,c},则A×B= 9.设集合A={a,b,c},A上的二元关系R={,},S={,, }则(R·S)= 10.数组{1,2,3,4}是一个能构成无向图的度数序列,此命题的真值是 8
4. 设G 条边 去G )条边,才能确定 G的一棵生 成树. A.m-n B. n-m C. m+ D. n-m+1 5. 图G 是欧 ). A. 数全 B. C. 连通且 结点 数全 偶数 D. 且所有 数全 |得分!评巷人 I . I I 二、填空题(每小题 4分,共 0分} 6. :x ,G(x):x 命题 号化 7. 公式 --. 取范 8. 集合 1, 则IAXB 1= 9. 合A= ,A 系R = { ,} ,S= { ,, } • S)= 10. {l ,2 ,3 ,4} 掬成 序列 命题 值是 8

得分 评卷人 三、化简计算题(每小题10分,共50分) 11.判断命题公式(Q→P)ΛP的类型(重言式、矛盾式或可满足式). 12.试作以下二题: (1)设A={1,2},B={a,b},试问从A到B的二元关系有多少个?试写出其中是从A到 B的函数的二元关系。 (2)设f,g都是R→R的函数;Vx∈R,f(x)=x3-1,g(x)=x2+1.指出f,g哪个是双 射函数(可以不证明),求其反函数 13.化简集合表达式(AUB)∩B)-(CUB)U(AUB)∩~B)UA) 14.设有向图D(如图2), (1)求邻接矩阵A(D); (2)已知 00211 00137 0001 0011 A2(D)= A3(D)= 0011 00 12 0012 00 23 求从w1到v,长度为3的通路有几条?v,到自身长度为2的回路有几条? 图2第14题图 9
|得分|评卷人| I I I 三、化筒计算题{每小题 1. Q→P) 八P 矛盾式或可 12. 下二 (1)设 {1.2} ,B= {a. 二元 有多 二元关 (2) 是R→R 的 =x3 -1 , g ( x ) =x2 +1. j, 射函数(可以不证明) ,求其反函数. 13. 合表达 U B B) B) U «(AUB) n~B) UA). 14. 设有 图D( (1)求邻接矩阵 (2) 002 1 000 1 A2 (D) = 001 1 001 2 001 3 o 0 1 1 001 2 002 3 求从 I到叫长度为 3的通路有几条?叫到自身长度为 2的回路有几条? 4题图 9
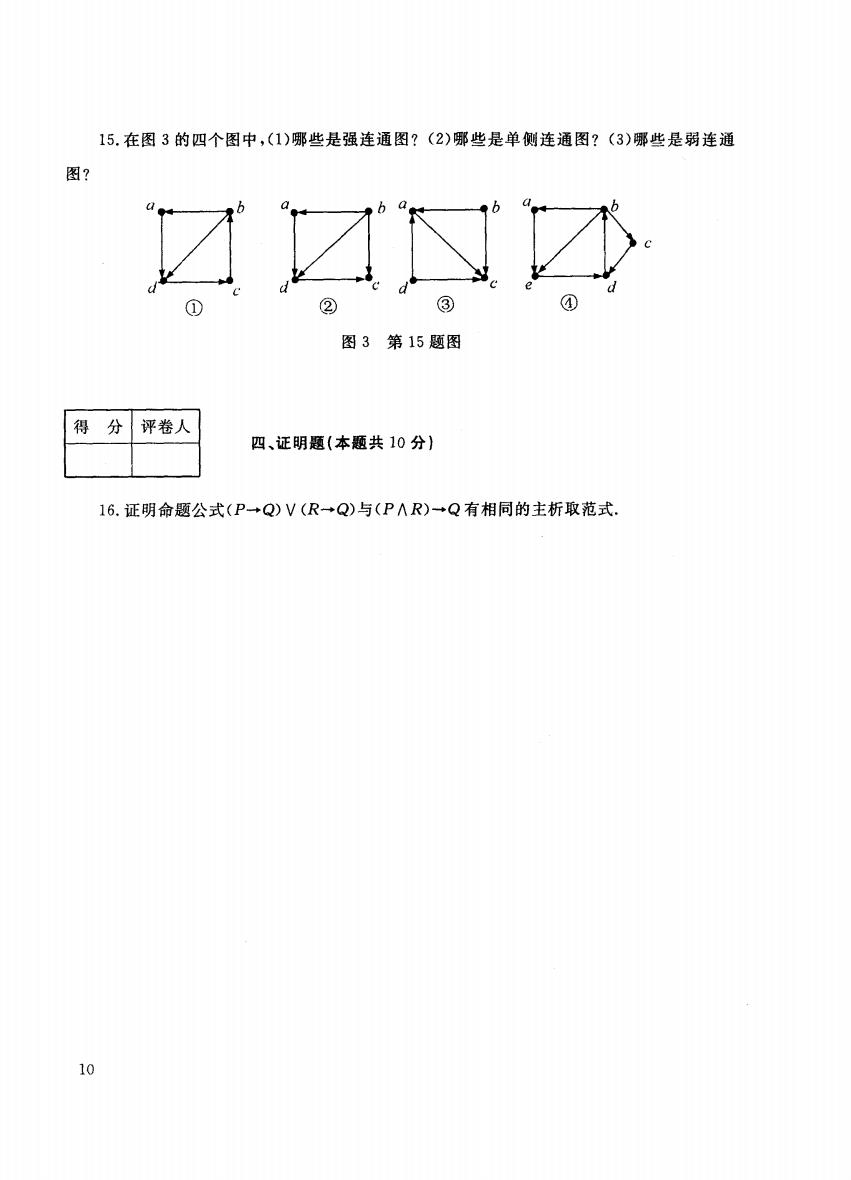
15.在图3的四个图中,(1)哪些是强连通图?(2)哪些是单侧连通图?(3)哪些是弱连通 图? ☑☑还 图3第15题图 得分 评卷人 四、证明题(本题共10分) 16.证明命题公式(P+Q)V(R→Q)与(P∧R)+Q有相同的主析取范式. 10
15. 图3 (1 些是 连通 (2) 是单侧连通 (3) 图? .k |得分|评卷人| 1-- I I 四、证明题(本题共 0分} 16. 命题 10

试卷代号:1002 中央广播电视大学2011一2012学年度第一学期“开放本科”期末考试(半开卷) 计算机数学基础(1)试题答案及评分标准 (供参考) 2012年1月 一、单项选择题(每小题4分,共20分)】 1.B 2.D 3.C 4.A 5.C 二、填空题(每小题4分,共20分)】 6.Hx(F(x)→+G(x) 7.P∧Q 8.12 9.{,} 10.1 三、化简计算题(每小题10分,共50分】 11.解:-(Q→P)∧P台(QVP)∧P 台(QAP)∧P (4分) 台Q∧P∧P 台Q∧(P∧P) QΛ0台0 (8分) 所以一(Q一P)∧P是矛盾式(永假式) (10分) 12.解:(1)二元关系共有16个.其中是函数的有4个分别为 {,},{,}, {,},{,} (5分) (2)f是双射函数,其反函数为f-1=x+1 (10分) 13.解:((AUB)∩B)-(CUB))U((AUB)∩~B)UA) =(B∩~C∩~B)U((A∩~B)UA) (7分) =⑦UA=A (10分) 11
试卷代号 中央广播电视大学 11 2学年度第-学期"开放本科"期末考试(半开卷) 计算机数学基础 )试题答案及评分标准 (供参考) 2012 年1 一、单项选择题{每小题 4分,共 0分} 1. B 2. D 3. C 二、填空题{每小题 4分,共 0分} 6. 'v x(F(x)•G(x)) 7.P -, 8. 12 9. { ,} 10. 1 4.A 5. C 三、化简计算题{每小题 0分,共 0分} 1. -, /\P -, -, P) -, -, /\ (-, 所以 -, P是矛盾式(永假式). 12. (1 有16 有4 个分别 为 { , }, { { , }, { , } (2)/ 是双射 =非 13. ( ( (A U B) n B) 一(CUB)) U (((A U B) n ~B) UA) =(Bn~C U ((A 门~B) UA) =(UA = A (4 (8 (1 0 (5 (1 (7 (1

02107 0 0 01 14.解:(1)A(D)= (5分) 0001 011 0 (2)从1到v4长度为3的通路有3条,,到自身长度为2的回路2条. (10分) 15.解:(1)①,④是强连通图: (4分) (2)①,②,④(或只答②)是单侧连通图; (7分) (3)①,②,③,④(或只答③)是弱连通图. (10分) 四、证明题(本题共10分) 16.证:方法1. (P→Q)V(R+Q)台(-PVQ)V(-RVQ) (PAR)VQH(P∧R)→Q (6分) 因为两命题公式等值,由主合取范式的惟一性,可知两命题公式的主合取范式是相同.(10分) 方法2 (P-Q)V(R-Q)(-PVQ)V(-RVQ) PV-RVQ-PVQV-R (4分) (P∧R)→QPV-RVQH-PVQV-R (8分) 因为它们的主合取范式相同,可知它们的主析取范式也相同. (10分) 12
(4 (8 (1 (1 (4 (7 (1 (5 (2) 长度为3 的 有3 为2 路2 15. (1 ④是强连通 (2) 是单侧 (3)①,②,③,④(或只答③〉是弱连通图. 四、证明题{本题共 16. 1. (P→Q)V(R→Q) ...., VQ) V (....,R V Q) ...., I\ R ) V I\ R )• Q (6 因为两命题公式等值,由主合取范式的惟一性,可知两命题公式的主合取范式是相同.(1 方法 (P →Q)V(R→Q) ....,PVQ) V (....,R V Q) -. ....,R 件-.PVQV ....,R (P I\ -. ....,R -. -.R 因为它们的主合取范式相同,可知它们的主析取范式也相同. 12