第五章树与二叉树 5.1树的定义及基本术语 5.1.1树的定义 A B E F 图5.1树的示例 PT PRESS 退出
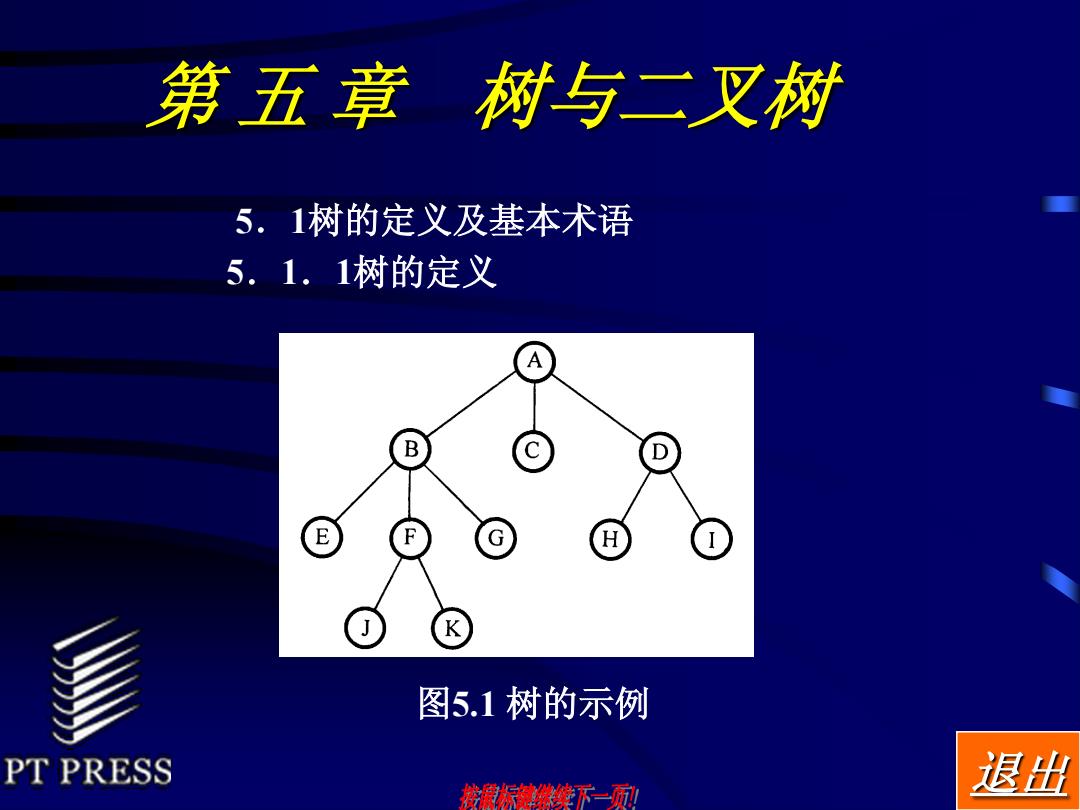
第 五 章 树与二叉树 5.1树的定义及基本术语 5.1.1树的定义 退出 图5.1 树的示例

A A B B D E F F © @ © G C (a) D H A(B(E,F(J,K),G),C,D(H,I)) (b) (c) 图5.2 PT PRESS 然东续了一列
图5.2

5.1.2基本术语 1、根 2、度(结点的度和树的度) 3、叶 4、分枝结点 5、双亲、子女、祖先、子孙 6、兄弟、堂兄弟 7、结点的层次、树的深度(高度) 8、有序树、无序树 9、森林 PT PRESS 然东续了一列
5.1.2基本术语 1、根 2、度(结点的度和树的度) 3、叶 4、分枝结点 5、双亲、子女、祖先、子孙 6、兄弟、堂兄弟 7、结点的层次、树的深度(高度) 8、有序树、无序树 9、森林

1.2二叉树 5.2.1二叉树的性质 (1)在二叉树的第上至多有21个结点 (>=1) (2)深度为k的二叉树至多有2k1个结点。 (3)设任何一棵二叉树中,叶结点数为n0,度为1的 结点数为n1,度为2的结点数为n2,则有:n0=n2+1 (4)具有个结点的完全二叉树其深度为:k= [l0g2n]+1 (应改为底函数) PT PRESS 按续不一列
1.2二叉树 5.2.1二叉树的性质 (1) 在二叉树的第i上至多有2 i-1个结点(i>=1) (2) 深度为k的二叉树至多有2 k -1个结点。 (3) 设任何一棵二叉树中,叶结点数为n0,度为1 的 结点数为n1,度为2的结点数为n2,则有:n0=n2+1 (4) 具有n个结点的完全二叉树其深度为:k= [log2n]+1 ([]应改为底函数)

(5)对于具有个结点的完全二叉树有如下特点: ①i=1则是树根,若>1则它的双亲为i/2(取整); ②如果2i>n则没有左子女,否则它的左子女为2i; ③如果2i+1>n则没有右子女,否则它的右子女为 2it1; PT PRESS 然东续下一
(5)对于具有n个结点的完全二叉树有如下特点: ①i=1则是树根,若i>1则它的双亲为i/2(取整); ②如果2i>n 则 i没有左子女,否则它的左子女为2i; ③如果2i+1>n 则 i没有右子女,否则它的右子女为 2i+1;

10 11 12 13 14 15 10 12 (a)满二叉树 (b)完全二叉树 图5-3 PT PRESS 然东续了一 n
图5-3

5.2.2二叉树的存储结构 1、顺序存储 顺序存储的二叉树的定义如下: #define N50/*树结点的最大个数*/ typedef elemtype SQTREE[N]; PT PRESS 然东续下一
5.2.2 二叉树的存储结构 1、顺序存储 顺序存储的二叉树的定义如下: #define N 50 /*树结点的最大个数*/ typedef elemtype SQTREE[N];
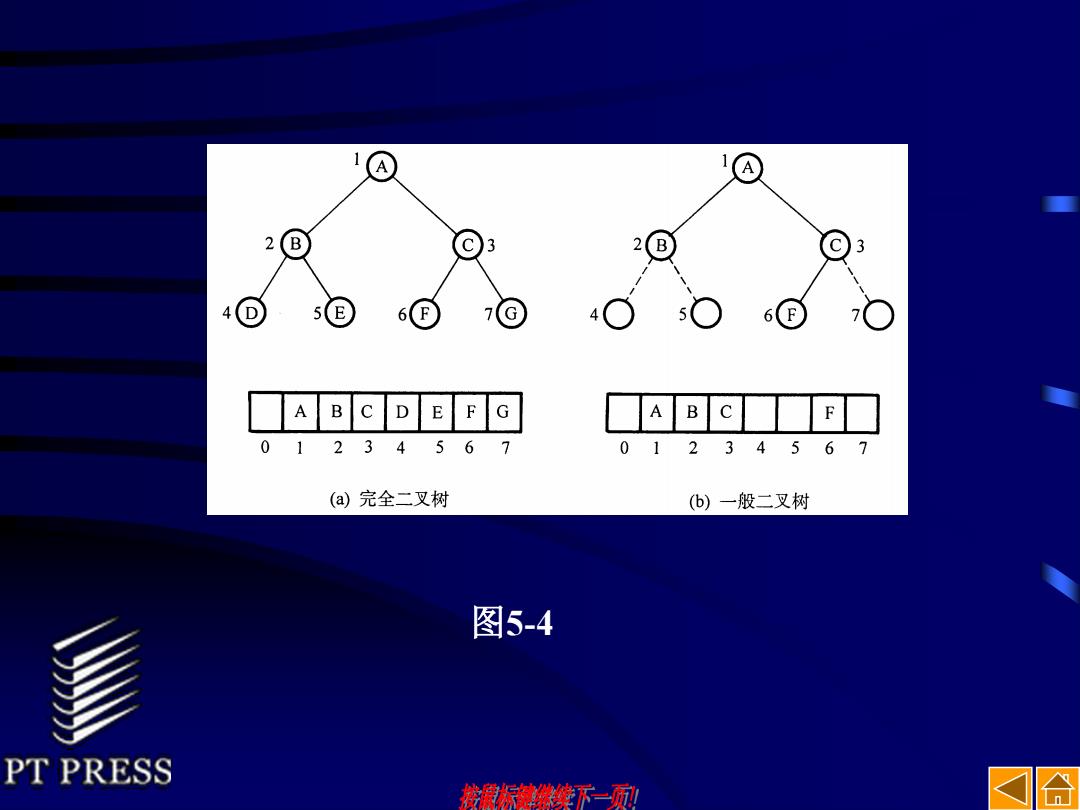
A 1 2 B 3 4 (D E 6 F G ■A B C D E P G ABC■■E 01234567 01234567 (a)完全二叉树 (b)一般二叉树 图5-4 PT PRESS 然东续了一列 n
图5-4
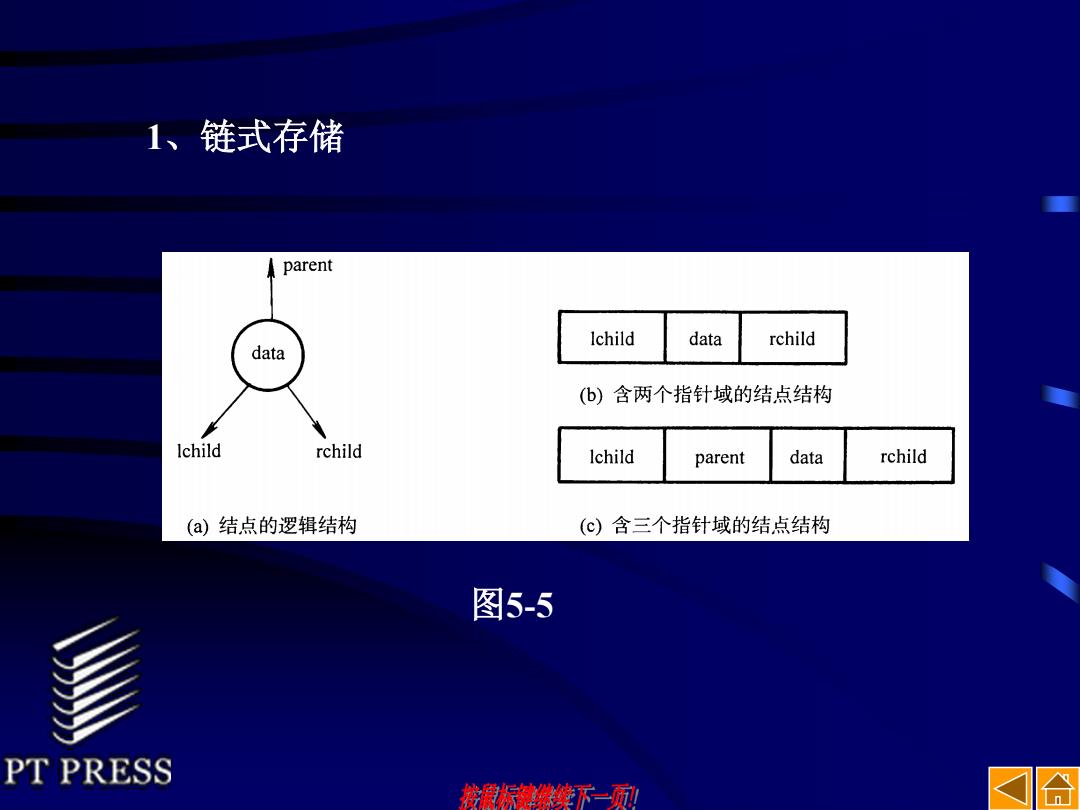
1、链式存储 parent Ichild data rchild data (b)含两个指针域的结点结构 Ichild rchild Ichild parent data rchild (a)结点的逻辑结构 (c)含三个指针域的结,点结构 图5-5 PT PRESS 然东续了一 n
1、链式存储 图5-5
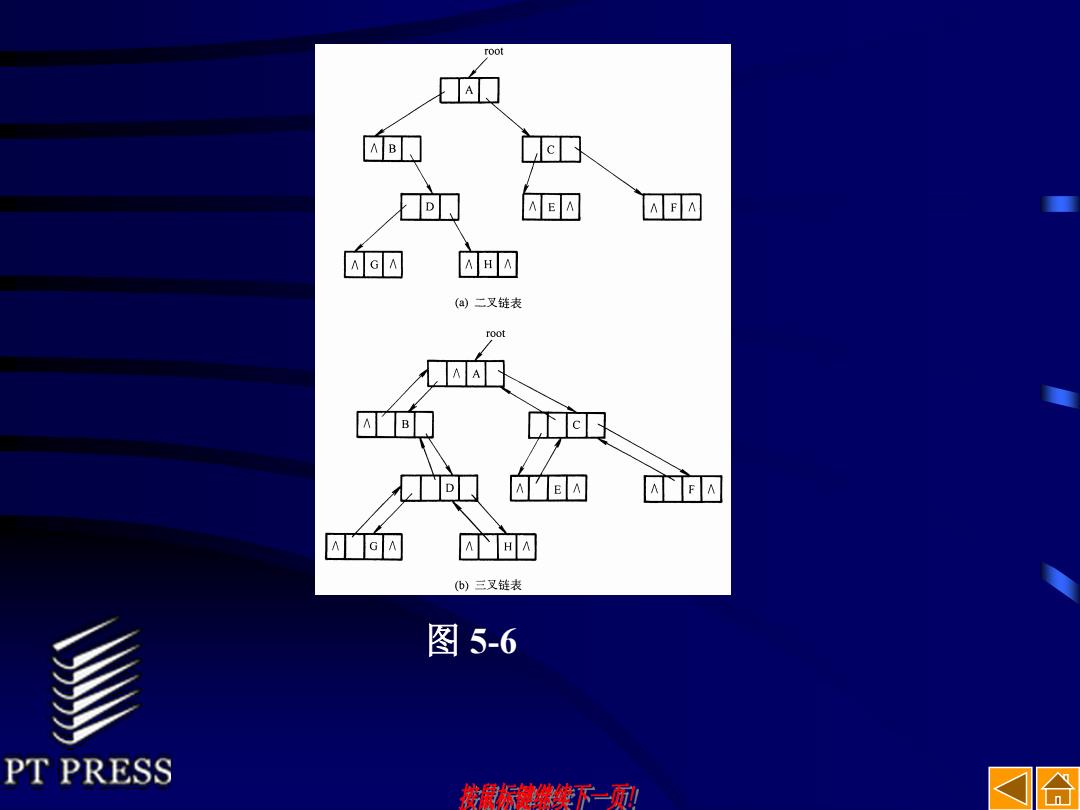
root A A GA 回N (a)二叉链表 root B D AHA (b)三叉链表 图5-6 PT PRESS 然东续了一 n
图 5-6